Inštrukcie

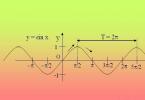
Najmenej pozitívne obdobie kosínus sa tiež rovná 2?. Zvážte to dôkazom na príklade funkcie y=cos(x). Ak je T ľubovoľné obdobie om kosínus, potom cos(a+T)=cos(a). V prípade, že a=0, cos(T)=cos(0)=1. Vzhľadom na to je najmenšia kladná hodnota T, pri ktorej cos(x) = 1, 2?.

Vzhľadom na skutočnosť, že 2? – obdobie sínus a kosínus, bude tiež obdobie ohm kotangens, rovnako ako dotyčnica, ale nie minimálna, pretože, ako je najmenší klad obdobie dotyčnica a kotangens sú rovnaké?. Môžete to overiť zvážením nasledujúceho: body zodpovedajúce (x) a (x+?) na trigonometrickej kružnici majú diametrálne opačné polohy. Vzdialenosť od bodu (x) k bodu (x+2?) zodpovedá polovici kruhu. Podľa definície tangens a kotangens tg(x+?)=tgx a ctg(x+?)=ctgx, čo znamená najmenší kladný obdobie kotangens a ?.

Poznámka

Nezamieňajte funkcie y=cos(x) a y=sin(x) - majúce rovnakú bodku, tieto funkcie sú reprezentované odlišne.

Užitočné rady

Pre väčšiu prehľadnosť nakreslite goniometrickú funkciu, pre ktorú je vypočítaná najmenšia kladná perióda.

Zdroje:

• Príručka matematiky, školská matematika, vyššia matematika

Trigonometrické funkcie periodické, to znamená, že sa po určitom období opakujú. Vďaka tomu stačí naštudovať funkciu na tomto intervale a zistené vlastnosti rozšíriť na všetky ďalšie obdobia.

Inštrukcie

Ak chcete nájsť periódu goniometrickej funkcie umocnenej na mocninu, vyhodnoťte paritu mocniny. Skrátiť štandardnú lehotu na polovicu. Napríklad, ak dostanete funkciu y=3 cos^2x, potom sa štandardná perióda 2P zníži 2-krát, takže perióda sa bude rovnať P. Upozorňujeme, že funkcie tg, ctg sú periodické k P až ľubovoľnému stupňa.

Zo školských hodín matematiky si každý pamätá sínusový graf tiahnuci sa do diaľky v rovnomerných vlnách. Mnoho ďalších funkcií má podobnú vlastnosť - opakovanie po určitom intervale. Nazývajú sa periodické. Periodicita je veľmi dôležitá vlastnosť funkcie, s ktorou sa často stretávame pri rôznych úlohách. Preto je užitočné vedieť určiť, či je funkcia periodická.

Inštrukcie

Ak je F(x) funkciou argumentu x, potom sa nazýva periodický, ak existuje číslo T také, že pre ľubovoľné x platí F(x + T) = F(x). Toto číslo T sa nazýva perióda funkcie.

Období môže byť niekoľko. Napríklad funkcia F = const nadobúda rovnakú hodnotu pre akúkoľvek hodnotu argumentu, a preto za jej bodku možno považovať akékoľvek číslo.

Matematikov zvyčajne zaujíma najmenšia nenulová perióda funkcie. Pre stručnosť sa tomu hovorí jednoducho obdobie.

Klasickým príkladom periodických funkcií je goniometrické: sínus, kosínus a tangens. Ich perióda je rovnaká a rovná sa 2?, teda sin(x) = sin(x + 2?) = sin(x + 4?) atď. Samozrejme, goniometrické funkcie nie sú jediné periodické.

V prípade jednoduchých základných funkcií je jediným spôsobom, ako určiť, či sú periodické alebo neperiodické, pomocou výpočtu. Ale pre zložité funkcie už existuje niekoľko jednoduchých pravidiel.

Ak je F(x) periodická funkcia s periódou T a je pre ňu definovaná derivácia, potom táto derivácia f(x) = F?(x) je tiež periodická funkcia s periódou T. Koniec koncov, hodnota derivácia v bode x sa rovná dotyčnici grafu dotyčnicového uhla jej primitívnej derivácie v tomto bode k osi x, a keďže primitívna derivácia sa periodicky opakuje, derivácia sa musí tiež opakovať. Napríklad derivácia funkcie sin(x) sa rovná cos(x) a je periodická. Ak vezmete derivát cos(x), získate –sin(x). Frekvencia zostáva nezmenená.

Opak však nie je vždy pravdou. Funkcia f(x) = const je teda periodická, ale jej primitívna funkcia F(x) = const*x + C nie je.

Ak F(x) je periodická funkcia s periódou T, potom G(x) = a*F(kx + b), kde a, b, a k sú konštanty a k sa nerovná nule - je tiež periodická funkcia , a jej obdobie je T/k. Napríklad sin(2x) je periodická funkcia a jej perióda sa rovná?. Vizuálne to možno znázorniť takto: vynásobením x nejakým číslom sa zdá, že graf funkcie horizontálne stlačíte presne toľkokrát

Ak sú F1(x) a F2(x) periodické funkcie a ich periódy sa rovnajú T1 a T2, potom súčet týchto funkcií môže byť tiež periodický. Jeho obdobie však nebude jednoduchým súčtom období T1 a T2. Ak je výsledkom delenia T1/T2 racionálne číslo, potom súčet funkcií je periodický a jeho perióda sa rovná najmenšiemu spoločnému násobku (LCM) periód T1 a T2. Napríklad, ak je perióda prvej funkcie 12 a perióda druhej 15, potom sa perióda ich súčtu bude rovnať LCM (12, 15) = 60.

Vizuálne to možno znázorniť takto: funkcie prichádzajú s rôznymi „šírkami krokov“, ale ak je pomer ich šírok racionálny, potom sa skôr alebo neskôr (alebo skôr presne prostredníctvom LCM krokov) opäť zrovnajú a ich súčet začne nové obdobie.

Ak je však pomer období iracionálny, potom celková funkcia nebude vôbec periodická. Napríklad nech F1(x) = x mod 2 (zvyšok, keď x je delené 2) a F2(x) = sin(x). T1 sa tu bude rovnať 2 a T2 sa bude rovnať 2?. Je pomer období rovnaký? - iracionálne číslo. Preto funkcia sin(x) + x mod 2 nie je periodická.

Mnohé matematické funkcie majú jednu vlastnosť, ktorá uľahčuje ich konštrukciu: periodicita, teda opakovateľnosť grafu na súradnicovej sieti v pravidelných intervaloch.

Inštrukcie

Najznámejšie periodické funkcie v matematike sú funkcie sínus a kosínus. Tieto funkcie majú vlnový charakter a hlavnú periódu 2P. Tiež špeciálny prípad periodickej funkcie je f(x)=konšt. Pre pozíciu x je vhodné akékoľvek číslo, táto funkcia nemá hlavnú bodku, keďže ide o priamku.

Vo všeobecnosti je funkcia periodická, ak existuje celé číslo N, ktoré je nenulové a spĺňa pravidlo f(x)=f(x+N), čím sa zabezpečí opakovateľnosť. Perióda funkcie je najmenšie číslo N, ale nie nula. To znamená, že napríklad funkcia sin x sa rovná funkcii sin (x+2ПN), kde N=±1, ±2 atď.

Niekedy môže mať funkcia multiplikátor (napríklad sin 2x), ktorý zvýši alebo zníži periódu funkcie. Ak chcete nájsť obdobie podľa grafika, je potrebné určiť extrémy funkcie - najvyššie a najnižšie body grafu funkcie. Keďže sínusové a kosínusové vlny majú vlnovú povahu, je to celkom jednoduché. Z týchto bodov zostrojte kolmé priame čiary, kým sa nepretnú s osou X.

Vzdialenosť od horného extrému k spodnému bude polovica periódy funkcie. Najpohodlnejšie je vypočítať periódu od priesečníka grafu s osou Y a podľa toho nulovú značku na osi x. Potom musíte vynásobiť výslednú hodnotu dvoma a získať hlavnú periódu funkcie.

Pre zjednodušenie konštrukcie sínusových a kosínusových grafov si treba uvedomiť, že ak má funkcia celočíselnú hodnotu, tak sa jej perióda predĺži (to znamená, že 2P treba vynásobiť týmto koeficientom) a graf bude vyzerať jemnejší, hladší – a ak je číslo zlomkové, naopak, bude klesať a graf bude „ostrejší“ a má skákavý vzhľad.

Cieľ: zhrnúť a systematizovať vedomosti študentov na tému „Periodika funkcií“; rozvíjať zručnosti pri uplatňovaní vlastností periodickej funkcie, hľadaní najmenšej kladnej periódy funkcie, zostrojovaní grafov periodických funkcií; podporovať záujem o štúdium matematiky; kultivovať pozorovanie a presnosť.

Vybavenie: počítač, multimediálny projektor, karty úloh, diapozitívy, hodiny, tabuľky ozdôb, prvky ľudových remesiel

"Matematika je to, čo ľudia používajú na ovládanie prírody a seba."
A.N. Kolmogorov

Počas vyučovania

I. Organizačná etapa.

Kontrola pripravenosti žiakov na vyučovaciu hodinu. Oznámte tému a ciele lekcie.

II. Kontrola domácich úloh.

Kontrolujeme domáce úlohy pomocou vzoriek a diskutujeme o najťažších bodoch.

III. Zovšeobecňovanie a systematizácia poznatkov.

1. Ústna frontálna práca.

Problémy teórie.

1) Vytvorte definíciu periódy funkcie
2) Pomenujte najmenšiu kladnú periódu funkcií y=sin(x), y=cos(x)
3). Aká je najmenšia kladná perióda funkcií y=tg(x), y=ctg(x)
4) Pomocou kruhu dokážte správnosť vzťahov:

y=sin(x) = sin(x+360º)
y=cos(x) = cos(x+360º)
y=tg(x) = tg(x+18 0º)
y=ctg(x) = ctg(x+180º)

tg(x+π n)=tgx, n € Z
ctg(x+π n)=ctgx, n € Z

sin(x+2π n)=sinx, n € Z
cos(x+2π n)=cosx, n € Z

5) Ako vykresliť periodickú funkciu?

Ústne cvičenia.

1) Dokážte nasledujúce vzťahy

a) sin(740º) = sin(20º)
b) cos(54º) = cos(-1026º)
c) sin(-1000º) = sin(80º)

2. Dokážte, že uhol 540º je jednou z periód funkcie y= cos(2x)

3. Dokážte, že uhol 360º je jednou z periód funkcie y=tg(x)

4. Transformujte tieto výrazy tak, aby uhly v nich obsiahnuté nepresiahli 90º v absolútnej hodnote.

a) tg375º
b) ctg530º
c) sin1268º
d) cos(-7363º)

5. Kde ste sa stretli so slovami OBDOBIE, PERIODICITA?

Študent odpovedá: Obdobie v hudbe je štruktúra, v ktorej je prezentovaná viac-menej úplná hudobná myšlienka. Geologické obdobie je súčasťou éry a delí sa na epochy s obdobím od 35 do 90 miliónov rokov.

Polčas rozpadu rádioaktívnej látky. Periodický zlomok. Periodiká sú tlačené publikácie, ktoré vychádzajú v presne stanovených termínoch. Mendelejevov periodický systém.

6. Obrázky znázorňujú časti grafov periodických funkcií. Určte periódu funkcie. Určte periódu funkcie.

Odpoveď T = 2; T = 2; T = 4; T = 8.

7. Kde ste sa v živote stretli s konštrukciou opakujúcich sa prvkov?

Odpoveď žiaka: Prvky ornamentov, ľudové umenie.

IV. Kolektívne riešenie problémov.

(Riešenie problémov na snímkach.)

Uvažujme o jednom zo spôsobov, ako študovať funkciu pre periodicitu.

Táto metóda sa vyhýba ťažkostiam spojeným s dokazovaním, že určitá perióda je najmenšia, a tiež eliminuje potrebu dotýkať sa otázok o aritmetických operáciách s periodickými funkciami a periodicitou komplexnej funkcie. Úvaha je založená len na definícii periodickej funkcie a na nasledujúcej skutočnosti: ak T je perióda funkcie, potom nT(n?0) je jej perióda.

Úloha 1. Nájdite najmenšiu kladnú periódu funkcie f(x)=1+3(x+q>5)

Riešenie: Predpokladajme, že T-perióda tejto funkcie. Potom f(x+T)=f(x) pre všetky x € D(f), t.j.

1+3(x+T+0,25)=1+3(x+0,25)
(x+T+0,25)=(x+0,25)

Dajme x=-0,25 a dostaneme

(T) = 0<=>T=n, n € Z

Zistili sme, že všetky periódy príslušnej funkcie (ak existujú) patria medzi celé čísla. Z týchto čísel vyberme najmenšie kladné číslo. Toto 1 . Overme si, či to bude vlastne obdobie 1 .

f(x+1) = 3(x+1+0,25)+1

Keďže (T+1)=(T) pre ľubovoľné T, potom f(x+1)=3((x+0,25)+1)+1=3(x+0,25)+1=f(x), t.j. 1 – obdobie f. Keďže 1 je najmenšie zo všetkých kladných celých čísel, potom T=1.

Úloha 2. Ukážte, že funkcia f(x)=cos 2 (x) je periodická a nájdite jej hlavnú periódu.

Úloha 3. Nájdite hlavnú periódu funkcie

f(x)=sin(1,5x)+5cos(0,75x)

Predpokladajme T-periódu funkcie, potom pre ľubovoľnú X pomer platí

sin1,5(x+T)+5cos0,75(x+T)=sin(1,5x)+5cos(0,75x)

Ak x = 0, potom

sin(1,5T)+5cos(0,75T)=sin0+5cos0

sin(1,5T)+5cos(0,75T)=5

Ak x=-T, potom

sin0+5cos0=sin(-1,5T)+5cos0,75(-T)

5= – sin(1,5T)+5cos(0,75T)

sin(1,5T)+5cos(0,75T)=5 – sin(1,5T)+5cos(0,75T)=5

Keď to spočítame, dostaneme:

10 cos (0,75 T) = 10

2π n, n € Z

Vyberme si najmenšie kladné číslo zo všetkých „podozrivých“ čísel pre periódu a skontrolujeme, či ide o bodku pre f. Toto číslo

f(x+)=sin(1,5x+4π)+5cos(0,75x+2π)= sin(1,5x)+5cos(0,75x)=f(x)

To znamená, že ide o hlavné obdobie funkcie f.

Úloha 4. Skontrolujeme, či je funkcia f(x)=sin(x) periodická

Nech T je perióda funkcie f. Potom pre ľubovoľné x

sin|x+Т|=sin|x|

Ak x=0, potom sin|Т|=sin0, sin|Т|=0 Т=π n, n € Z.

Predpokladajme. Že pre niektoré n je číslo π n periódou

uvažovaná funkcia π n>0. Potom sin|π n+x|=sin|x|

To znamená, že n musí byť párne aj nepárne číslo, ale to nie je možné. Preto táto funkcia nie je periodická.

Úloha 5. Skontrolujte, či je funkcia periodická

f(x)=

Nech T je obdobie f

, teda sinT=0, Т=π n, n € Z. Predpokladajme, že pre nejaké n je číslo π n skutočne periódou tejto funkcie. Potom číslo 2π n bude bodka

Keďže čitatelia sú si rovní, ich menovatelia sú si rovní

To znamená, že funkcia f nie je periodická.

Pracovať v skupinách.

Úlohy pre skupinu 1.

Úlohy pre skupinu 2.

Skontrolujte, či je funkcia f periodická a nájdite jej základnú periódu (ak existuje).

f(x)=cos(2x)+2sin(2x)

Úlohy pre skupinu 3.

Na konci svojej práce skupiny prezentujú svoje riešenia.

VI. Zhrnutie lekcie.

Reflexia.

Učiteľ rozdá študentom kartičky s kresbami a požiada ich, aby vyfarbili časť prvej kresby v súlade s tým, do akej miery si myslia, že zvládli metódy štúdia funkcie pre periodicitu, a časť druhej kresby - v súlade s ich príspevok k práci na vyučovacej hodine.

VII. Domáca úloha

1). Skontrolujte, či je funkcia f periodická a nájdite jej základnú periódu (ak existuje)

b). f(x)=x2-2x+4

c). f(x)=2tg(3x+5)

2). Funkcia y=f(x) má periódu T=2 a f(x)=x 2 +2x pre x € [-2; 0]. Nájdite hodnotu výrazu -2f(-3)-4f(3,5)

Literatúra/

1. Mordkovich A.G. Algebra a začiatky analýzy s hĺbkovým štúdiom.
2. Matematika. Príprava na jednotnú štátnu skúšku. Ed. Lysenko F.F., Kulabukhova S.Yu.
3. Sheremeteva T.G. , Tarasová E.A. Algebra a počiatočná analýza pre ročníky 10-11.

Zo školských hodín matematiky si každý pamätá sínusový graf tiahnuci sa do diaľky v rovnomerných vlnách. Mnoho ďalších funkcií má podobnú vlastnosť - opakovanie v určitom intervale. Nazývajú sa periodické. Periodicita je veľmi významná kvalita funkcie, ktorá sa často vyskytuje v rôznych úlohách. Preto je výhodné vedieť určiť, či je funkcia periodická.

Inštrukcie

1. Ak je F(x) funkciou argumentu x, potom sa nazýva periodický, ak existuje číslo T také, že pre každé x platí F(x + T) = F(x). Toto číslo T sa nazýva perióda funkcie. Období môže byť niekoľko. Povedzme, že funkcia F = const má rovnakú hodnotu pre všetky hodnoty argumentu, a preto za jej periódu možno považovať akékoľvek číslo Tradične sa matematika zaoberá minimálnou nenulovou periódou funkcie. Pre stručnosť sa to nazýva primitívne obdobie.

2. Typickým príkladom periodických funkcií je goniometrické: sínus, kosínus a tangens. Ich perióda je identická a rovná sa 2?, teda sin(x) = sin(x + 2?) = sin(x + 4?) atď. Samozrejme, goniometrické funkcie nie sú výlučne periodické.

3. Pokiaľ ide o primitívne, základné funkcie, jedinou metódou na určenie ich periodicity alebo neperiodicity sú výpočty. Ale pre zložité funkcie už existuje niekoľko primitívnych pravidiel.

4. Ak F(x) je periodická funkcia s periódou T a je pre ňu definovaná derivácia, potom táto derivácia f(x) = F?(x) je tiež periodická funkcia s periódou T. Hodnota derivácie v bode x sa rovná dotyčnici tangensového uhla grafu jeho primitívnej derivácie v tomto bode k osi x, a keďže primitívna derivácia sa periodicky opakuje, derivácia sa musí tiež opakovať. Povedzme, že derivácia funkcie sin(x) sa rovná cos(x) a je periodická. Ak vezmete derivát cos(x), získate –sin(x). Periodicita zostáva konštantná Avšak opak nie je vždy pravdou. Funkcia f(x) = const je teda periodická, ale jej primitívna funkcia F(x) = const*x + C nie je.

5. Ak F(x) je periodická funkcia s periódou T, potom G(x) = a*F(kx + b), kde a, b, a k sú konštanty a k sa nerovná nule - je tiež periodická funkcia , a jej obdobie je T/k. Povedzme, že sin(2x) je periodická funkcia a jej perióda sa rovná?. Vizuálne to možno znázorniť takto: vynásobením x ľubovoľným číslom sa zdá, že graf funkcie horizontálne stlačíte presne toľkokrát

6. Ak sú F1(x) a F2(x) periodické funkcie a ich periódy sa rovnajú T1 a T2, potom súčet týchto funkcií môže byť tiež periodický. Jeho obdobie však nebude jednoduchým súčtom období T1 a T2. Ak je výsledkom delenia T1/T2 primerané číslo, potom súčet funkcií je periodický a jeho perióda sa rovná najmenšiemu univerzálnemu násobku (LCM) periód T1 a T2. Povedzme, že ak je perióda prvej funkcie 12 a perióda 2. je 15, potom sa perióda ich súčtu bude rovnať LCM (12, 15) = 60. Vizuálne to možno znázorniť takto: funkcie prichádzajú s rôznymi „šírkami krokov“, ale ak je pomer ich šírky zmysluplný, potom sa skôr alebo neskôr (alebo skôr presne prostredníctvom LCM krokov) opäť zrovnajú a ich súčet začne nové obdobie.

7. Ak je však pomer období iracionálny, potom celková funkcia nebude vôbec periodická. Povedzme, že F1(x) = x mod 2 (zvyšok delenia x 2) a F2(x) = sin(x). T1 sa tu bude rovnať 2 a T2 sa bude rovnať 2?. Je pomer období rovnaký? - iracionálne číslo. V dôsledku toho funkcia sin(x) + x mod 2 nie je periodická.

Mnohé matematické funkcie majú jednu špecifickú vlastnosť, ktorá uľahčuje ich konštrukciu: periodicita, teda opakovateľnosť grafu na súradnicovej sieti v rovnakých intervaloch.

Inštrukcie

1. Najznámejšie periodické funkcie v matematike sú sínus a kosínus. Tieto funkcie majú vlnovú povahu a pivotnú periódu rovnajúcu sa 2P. Tiež špeciálny prípad periodickej funkcie je f(x)=konšt. Ľubovoľné číslo sa hodí na pozíciu x táto funkcia nemá hlavnú bodku, pretože je to priamka.

2. Vo všeobecnosti je funkcia periodická, ak existuje celé číslo N, ktoré je nenulové a spĺňa pravidlo f(x)=f(x+N), čím sa zabezpečí opakovateľnosť. Perióda funkcie je najmenšie číslo N, ale nie nula. To znamená, že funkcia sin x sa rovná funkcii sin (x+2ПN), kde N=±1, ±2 atď.

3. Príležitostne môže mať funkcia násobiteľ (povedzme sin 2x), ktorý zvýši alebo zníži periódu funkcie. Aby bolo možné zistiť obdobie podľa grafika, musíte určiť extrémy funkcie - najvyššie a najnižšie body grafu funkcie. Pretože sínusové a kosínusové vlny majú vlnovú povahu, je to celkom jednoduché. Z týchto bodov zostrojte kolmé priame čiary, kým sa nepretnú s osou X.

4. Vzdialenosť od horného extrému k spodnému bude polovica periódy funkcie. Pre každého je pohodlnejšie vypočítať obdobie od priesečníka grafu s osou Y a podľa toho nulovú značku na osi x. Potom musíte vynásobiť výslednú hodnotu dvoma a získať pivotnú periódu funkcie.

5. Aby ste uľahčili vykresľovanie sínusových a kosínusových kriviek, musíte si uvedomiť, že ak má funkcia celočíselné hodnoty, jej perióda sa predĺži (to znamená, že 2P sa musí vynásobiť týmto indikátorom) a graf bude vyzerať jemnejší a hladší. ; a ak je číslo zlomkové, naopak, bude klesať a graf bude „ostrejší“ a bude vyzerať ako skok.

Video k téme

Zo školských hodín matematiky si každý pamätá sínusový graf tiahnuci sa do diaľky v rovnomerných vlnách. Mnoho ďalších funkcií má podobnú vlastnosť - opakovanie po určitom intervale. Nazývajú sa periodické. Periodicita je veľmi dôležitá vlastnosť funkcie, s ktorou sa často stretávame pri rôznych úlohách. Preto je užitočné vedieť určiť, či je funkcia periodická.

Inštrukcie

• Ak je F(x) funkciou argumentu x, potom sa nazýva periodický, ak existuje číslo T také, že pre ľubovoľné x platí F(x + T) = F(x). Toto číslo T sa nazýva perióda funkcie. Období môže byť niekoľko. Napríklad funkcia F = const má rovnakú hodnotu pre akúkoľvek hodnotu argumentu, a preto za jej periódu možno považovať akékoľvek číslo. Matematici sa zvyčajne zaujímajú o najmenšiu nenulovú periódu funkcie. Pre stručnosť sa tomu hovorí jednoducho obdobie.
• Klasickým príkladom periodických funkcií je goniometrické: sínus, kosínus a tangens. Ich perióda je rovnaká a rovná sa 2π, to znamená sin(x) = sin(x + 2π) = sin(x + 4π) atď. Samozrejme, goniometrické funkcie nie sú jediné periodické.
• V prípade jednoduchých základných funkcií je jediným spôsobom, ako určiť, či sú periodické alebo neperiodické, pomocou výpočtu. Ale pre zložité funkcie už existuje niekoľko jednoduchých pravidiel.
• Ak je F(x) periodická funkcia s periódou T a je pre ňu definovaná derivácia, potom táto derivácia f(x) = F′(x) je tiež periodická funkcia s periódou T. Koniec koncov, hodnota derivácia v bode x sa rovná dotyčnici grafu dotyčnicového uhla jej primitívnej derivácie v tomto bode k osi x, a keďže primitívna derivácia sa periodicky opakuje, derivácia sa musí tiež opakovať. Napríklad derivácia funkcie sin(x) sa rovná cos(x) a je periodická. Ak vezmete derivát cos(x), získate –sin(x). Frekvencia zostáva nezmenená, opak však nie je vždy pravdou. Funkcia f(x) = const je teda periodická, ale jej primitívna funkcia F(x) = const*x + C nie je.
• Ak F(x) je periodická funkcia s periódou T, potom G(x) = a*F(kx + b), kde a, b, a k sú konštanty a k sa nerovná nule - je tiež periodická funkcia , a jeho obdobie je T/k. Napríklad sin(2x) je periodická funkcia a jej perióda je π. Vizuálne to možno znázorniť takto: vynásobením x nejakým číslom sa zdá, že graf funkcie vodorovne stlačíte presne toľkokrát
• Ak sú F1(x) a F2(x) periodické funkcie a ich periódy sa rovnajú T1 a T2, potom súčet týchto funkcií môže byť tiež periodický. Jeho obdobie však nebude jednoduchým súčtom období T1 a T2. Ak je výsledkom delenia T1/T2 racionálne číslo, potom súčet funkcií je periodický a jeho perióda sa rovná najmenšiemu spoločnému násobku (LCM) periód T1 a T2. Ak je napríklad perióda prvej funkcie 12 a perióda druhej 15, potom sa perióda ich súčtu bude rovnať LCM (12, 15) = 60. Vizuálne to možno znázorniť takto: funkcie prichádzajú s rôznymi „šírkami krokov“, ale ak je pomer ich šírok racionálny, potom sa skôr alebo neskôr (alebo skôr presne prostredníctvom LCM krokov) opäť zrovnajú a ich súčet začne nové obdobie.
• Ak je však pomer období iracionálny, potom celková funkcia nebude vôbec periodická. Napríklad nech F1(x) = x mod 2 (zvyšok, keď x je delené 2) a F2(x) = sin(x). T1 sa tu bude rovnať 2 a T2 sa bude rovnať 2π. Pomer periód sa rovná π - iracionálne číslo. Preto funkcia sin(x) + x mod 2 nie je periodická.