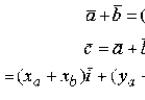În acest articol, vom acoperi:

• ce sunt vectorii coliniari;
• care sunt condițiile pentru vectorii coliniari;
• care sunt proprietățile vectorilor coliniari;
• care este dependența liniară a vectorilor coliniari.

Definiția 1

Vectorii coliniari sunt vectori care sunt paraleli cu aceeași linie sau se află pe aceeași linie.

Exemplul 1

Condiții pentru vectorii coliniari

Doi vectori sunt coliniari dacă oricare dintre următoarele condiții este adevărată:

• starea 1 . Vectorii a și b sunt coliniari dacă există un număr λ astfel încât a = λ b ;
• starea 2 . Vectorii a și b sunt coliniari cu raport egal de coordonate:

a = (a 1 ; a 2) , b = (b 1 ; b 2) ⇒ a ∥ b ⇔ a 1 b 1 = a 2 b 2

• starea 3 . Vectorii a și b sunt coliniari cu condiția ca produsul vectorial și vectorul zero să fie egali:

a ∥ b ⇔ a , b = 0

Observația 1

Condiția 2 nu se aplică dacă una dintre coordonatele vectoriale este zero.

Observația 2

Condiția 3 aplicabil numai acelor vectori care sunt dați în spațiu.

Exemple de probleme pentru studiul coliniarității vectorilor

Exemplul 1

Examinăm vectorii a \u003d (1; 3) și b \u003d (2; 1) pentru coliniaritate.

Cum să decizi?

În acest caz, este necesar să se folosească a doua condiție de coliniaritate. Pentru vectori dați, arată astfel:

Egalitatea este greșită. Din aceasta putem concluziona că vectorii a și b sunt necoliniari.

Răspuns : a | | b

Exemplul 2

Ce valoare m a vectorului a = (1 ; 2) și b = (- 1 ; m) este necesară pentru ca vectorii să fie coliniari?

Cum să decizi?

Folosind a doua condiție coliniară, vectorii vor fi coliniari dacă coordonatele lor sunt proporționale:

Aceasta arată că m = - 2 .

Răspuns: m = - 2 .

Criterii de dependență liniară și independență liniară a sistemelor de vectori

Teorema

Un sistem de vectori dintr-un spațiu vectorial este dependent liniar numai dacă unul dintre vectorii sistemului poate fi exprimat în termeni de restul vectorilor sistemului.

Dovada

Fie sistemul e 1 , e 2 , . . . , e n este dependent liniar. Să notăm combinația liniară a acestui sistem egală cu vectorul zero:

a 1 e 1 + a 2 e 2 + . . . + a n e n = 0

în care cel puţin unul dintre coeficienţii combinaţiei nu este egal cu zero.

Fie a k ≠ 0 k ∈ 1 , 2 , . . . , n .

Împărțim ambele părți ale egalității cu un coeficient diferit de zero:

a k - 1 (a k - 1 a 1) e 1 + (a k - 1 a k) e k + . . . + (a k - 1 a n) e n = 0

Denota:

A k - 1 a m , unde m ∈ 1 , 2 , . . . , k - 1 , k + 1 , n

În acest caz:

β 1 e 1 + . . . + β k - 1 e k - 1 + β k + 1 e k + 1 + . . . + βn e n = 0

sau e k = (- β 1) e 1 + . . . + (- β k - 1) e k - 1 + (- β k + 1) e k + 1 + . . . + (- β n) e n

Rezultă că unul dintre vectorii sistemului este exprimat în termenii tuturor celorlalți vectori ai sistemului. Ceea ce se cerea să fie dovedit (p.t.d.).

Adecvarea

Fie ca unul dintre vectori să fie exprimat liniar în termenii tuturor celorlalți vectori ai sistemului:

e k = γ 1 e 1 + . . . + γ k - 1 e k - 1 + γ k + 1 e k + 1 + . . . + γ n e n

Transferăm vectorul e k în partea dreaptă a acestei egalități:

0 = γ 1 e 1 + . . . + γ k - 1 e k - 1 - e k + γ k + 1 e k + 1 + . . . + γ n e n

Deoarece coeficientul vectorului e k este egal cu - 1 ≠ 0 , obținem o reprezentare netrivială a zero printr-un sistem de vectori e 1 , e 2 , . . . , e n , iar aceasta, la rândul său, înseamnă că sistemul dat de vectori este dependent liniar. Ceea ce se cerea să fie dovedit (p.t.d.).

Consecinţă:

• Un sistem de vectori este liniar independent atunci când niciunul dintre vectorii săi nu poate fi exprimat în termenii tuturor celorlalți vectori ai sistemului.
• Un sistem vectorial care conține un vector nul sau doi vectori egali este dependent liniar.

Proprietăți ale vectorilor liniar dependenți

1. Pentru vectorii 2- și 3-dimensionali, condiția este îndeplinită: doi vectori dependenți liniar sunt coliniari. Doi vectori coliniari sunt dependenți liniar.
2. Pentru vectorii tridimensionali, condiția este îndeplinită: trei vectori dependenți liniar sunt coplanari. (3 vectori coplanari - dependenti liniar).
3. Pentru vectorii n-dimensionali, condiția este îndeplinită: n + 1 vectori sunt întotdeauna dependenți liniar.

Exemple de rezolvare a problemelor pentru dependența liniară sau independența liniară a vectorilor

Exemplul 3

Să verificăm vectorii a = 3 , 4 , 5 , b = - 3 , 0 , 5 , c = 4 , 4 , 4 , d = 3 , 4 , 0 pentru independență liniară.

Soluţie. Vectorii sunt dependenți liniar deoarece dimensiunea vectorilor este mai mică decât numărul de vectori.

Exemplul 4

Să verificăm vectorii a = 1 , 1 , 1 , b = 1 , 2 , 0 , c = 0 , - 1 , 1 pentru independența liniară.

Soluţie. Găsim valorile coeficienților la care combinația liniară va fi egală cu vectorul zero:

x 1 a + x 2 b + x 3 c 1 = 0

Scriem ecuația vectorială sub forma uneia liniare:

x 1 + x 2 = 0 x 1 + 2 x 2 - x 3 = 0 x 1 + x 3 = 0

Rezolvăm acest sistem folosind metoda Gauss:

1 1 0 | 0 1 2 - 1 | 0 1 0 1 | 0 ~

Din a 2-a linie scădem prima, din a 3-a - prima:

~ 1 1 0 | 0 1 - 1 2 - 1 - 1 - 0 | 0 - 0 1 - 1 0 - 1 1 - 0 | 0 - 0 ~ 1 1 0 | 0 0 1 - 1 | 0 0 - 1 1 | 0 ~

Scădeți al 2-lea din prima linie, adăugați al 2-lea la a 3-a:

~ 1 - 0 1 - 1 0 - (- 1) | 0 - 0 0 1 - 1 | 0 0 + 0 - 1 + 1 1 + (- 1) | 0 + 0 ~ 0 1 0 | 1 0 1 - 1 | 0 0 0 0 | 0

Din soluție rezultă că sistemul are multe soluții. Aceasta înseamnă că există o combinație diferită de zero a valorilor unor astfel de numere x 1 , x 2 , x 3 pentru care combinația liniară a , b , c este egală cu vectorul zero. Prin urmare, vectorii a , b , c sunt dependent liniar. ​​​​​​​

Dacă observați o greșeală în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter

Vectorii, proprietățile lor și acțiunile cu ei

Vectori, acțiuni cu vectori, spațiu vectorial liniar.

Vectorii sunt o colecție ordonată a unui număr finit de numere reale.

Acțiuni: 1. Înmulțirea unui vector cu un număr: lambda * vector x \u003d (lamda * x 1, lambda * x 2 ... lambda * x n). (3.4, 0.7) * 3 \u003d (9, 12,0.21 )

2. Adunarea vectorilor (aparțin aceluiași spațiu vectorial) vector x + vector y \u003d (x 1 + y 1, x 2 + y 2, ... x n + y n,)

3. Vector 0=(0,0…0)---n E n – vector n-dimensional (spațiu liniar) x + vector 0 = vector x

Teorema. Pentru ca un sistem de n vectori dintr-un spațiu liniar n-dimensional să fie dependent liniar, este necesar și suficient ca unul dintre vectori să fie o combinație liniară a celorlalți.

Teorema. Orice set de n+ primul vector al spațiului liniar n-dimensional yavl. dependent liniar.

Adunarea vectorilor, multiplicarea vectorilor cu numere. Scăderea vectorilor.

Suma a doi vectori este vectorul direcționat de la începutul vectorului până la sfârșitul vectorului, cu condiția ca începutul să coincidă cu sfârșitul vectorului. Dacă vectorii sunt dați de expansiunile lor în termeni de vectori de bază, atunci adăugarea vectorilor adună coordonatele lor respective.

Să luăm în considerare acest lucru folosind exemplul unui sistem de coordonate carteziene. Lăsa

Să arătăm asta

Figura 3 arată că

Suma oricărui număr finit de vectori poate fi găsită folosind regula poligonului (Fig. 4): pentru a construi suma unui număr finit de vectori, este suficient să potriviți începutul fiecărui vector următor cu sfârșitul celui anterior. și construiți un vector care leagă începutul primului vector cu sfârșitul ultimului.

Proprietățile operației de adunare vectorială:

În aceste expresii m, n sunt numere.

Diferența de vectori se numește vector.Al doilea termen este un vector opus vectorului ca direcție, dar egal cu acesta ca lungime.

Astfel, operația de scădere vectorială este înlocuită cu operația de adunare

Vectorul, al cărui început se află la originea coordonatelor, iar sfârșitul în punctul A (x1, y1, z1), se numește vectorul rază al punctului A și se notează sau pur și simplu. Deoarece coordonatele sale coincid cu coordonatele punctului A, expansiunea sa în termeni de vectori are forma

Un vector care începe în punctul A(x1, y1, z1) și se termină în punctul B(x2, y2, z2) poate fi scris ca

unde r 2 este vectorul rază al punctului B; r 1 - vector raza punctului A.

Prin urmare, expansiunea vectorului în termeni de orte are forma

Lungimea sa este egală cu distanța dintre punctele A și B

MULTIPLICARE

Deci, în cazul unei probleme plate, produsul unui vector prin a = (ax; ay) și un număr b se găsește prin formula

a b = (ax b; ay b)

Exemplul 1. Aflați produsul vectorului a = (1; 2) cu 3.

3 a = (3 1; 3 2) = (3; 6)

Deci, în cazul unei probleme spațiale, produsul vectorului a = (ax; ay; az) și numărul b se găsește prin formula

a b = (ax b; ay b; az b)

Exemplul 1. Aflați produsul vectorului a = (1; 2; -5) cu 2.

2 a = (2 1; 2 2; 2 (-5)) = (2; 4; -10)

Produsul scalar al vectorilor și unde este unghiul dintre vectorii si ; dacă oricare, atunci

Din definiția produsului scalar rezultă că

unde, de exemplu, este valoarea proiecției vectorului pe direcția vectorului.

Pătratul scalar al unui vector:

Proprietățile produsului punct:

Punctează produsul în coordonate

Dacă Acea

Unghiul dintre vectori

Unghiul dintre vectori - unghiul dintre direcțiile acestor vectori (unghiul cel mai mic).

Produs vectorial (Produsul vectorial al doi vectori.)- este un pseudovector perpendicular pe planul construit de doi factori, care este rezultatul operației binare „înmulțire vectorială” pe vectori din spațiul euclidian tridimensional. Produsul nu este nici comutativ, nici asociativ (este anticomutativ) și este diferit de produsul scalar al vectorilor. În multe probleme de inginerie și fizică, este necesar să se poată construi un vector perpendicular pe două existente - produsul vectorial oferă această oportunitate. Produsul încrucișat este util pentru „măsurarea” perpendicularității vectorilor - lungimea produsului încrucișat a doi vectori este egală cu produsul lungimii lor dacă sunt perpendiculari și scade la zero dacă vectorii sunt paraleli sau antiparaleli.

Produsul vectorial este definit numai în spații tridimensionale și șapte-dimensionale. Rezultatul produsului vectorial, ca și produsul scalar, depinde de metrica spațiului euclidian.

Spre deosebire de formula de calcul a produsului scalar din coordonatele vectorilor dintr-un sistem de coordonate dreptunghiular tridimensional, formula pentru produsul vectorial depinde de orientarea sistemului de coordonate dreptunghiulare sau, cu alte cuvinte, de „chiralitatea” acestuia.

Coliniaritatea vectorilor.

Doi vectori nenuli (nu egali cu 0) sunt numiți coliniari dacă se află pe drepte paralele sau pe aceeași linie. Un sinonim este acceptabil, dar nu este recomandat - vectori „paraleli”. Vectorii coliniari pot fi dirijați în aceeași direcție („co-direcționați”) sau direcționați opus (în acest din urmă caz ​​sunt numiți uneori „anticoliniari” sau „antiparaleli”).

Produsul mixt al vectorilor ( a,b,c)- produsul scalar al vectorului a și produsul vectorial al vectorilor b și c:

(a,b,c)=a ⋅(b×c)

uneori se numește produsul scalar triplu al vectorilor, aparent datorită faptului că rezultatul este un scalar (mai precis, un pseudoscalar).

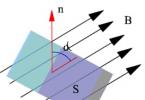
Semnificație geometrică: Modulul produsului mixt este numeric egal cu volumul paralelipipedului format de vectori (a,b,c) .

Proprietăți

Un produs mixt este simetric oblic în raport cu toate argumentele sale: adică e. o permutare a oricăror doi factori schimbă semnul produsului. Rezultă că produsul mixt în sistemul de coordonate carteziene drept (în bază ortonormală) este egal cu determinantul matricei compuse din vectori și:

Produsul mixt din sistemul de coordonate carteziene din stânga (în bază ortonormală) este egal cu determinantul unei matrice compusă din vectori și luată cu semnul minus:

În special,

Dacă oricare doi vectori sunt paraleli, atunci cu oricare al treilea vector formează un produs mixt egal cu zero.

Dacă trei vectori sunt dependenți liniar (adică, coplanari, se află în același plan), atunci produsul lor mixt este zero.

Sensul geometric - Produsul mixt în valoare absolută este egal cu volumul paralelipipedului (vezi figura) format din vectori și; semnul depinde dacă acest triplu de vectori este dreapta sau stânga.

Complanaritatea vectorilor.

Trei vectori (sau mai mulți) se numesc coplanari dacă ei, reducându-se la o origine comună, se află în același plan.

Proprietăți de complementaritate

Dacă cel puțin unul dintre cei trei vectori este zero, atunci cei trei vectori sunt de asemenea considerați coplanari.

Un triplu de vectori care conțin o pereche de vectori coliniari este coplanar.

Produs mixt al vectorilor coplanari. Acesta este un criteriu pentru coplanaritatea a trei vectori.

Vectorii coplanari sunt dependenți liniar. Acesta este, de asemenea, un criteriu de coplanaritate.

În spațiul tridimensional, 3 vectori necoplanari formează o bază

Vectori liniar dependenți și liniar independenți.

Sisteme de vectori liniar dependente și independente.Definiție. Sistemul de vectori se numește dependent liniar, dacă există cel puțin o combinație liniară netrivială a acestor vectori egală cu vectorul zero. Altfel, i.e. dacă doar o combinație liniară trivială de vectori dați este egală cu vectorul nul, vectorii sunt numiți liniar independent.

Teoremă (criteriul dependenței liniare). Pentru ca un sistem de vectori dintr-un spațiu liniar să fie dependent liniar, este necesar și suficient ca cel puțin unul dintre acești vectori să fie o combinație liniară a celorlalți.

1) Dacă există cel puțin un vector zero printre vectori, atunci întregul sistem de vectori este dependent liniar.

Într-adevăr, dacă, de exemplu, , atunci, presupunând , avem o combinație liniară netrivială .▲

2) Dacă unii dintre vectori formează un sistem dependent liniar, atunci întregul sistem este dependent liniar.

Într-adevăr, fie vectorii , , dependenți liniar. Prin urmare, există o combinație liniară netrivială egală cu vectorul zero. Dar apoi, presupunând , obținem și o combinație liniară netrivială egală cu vectorul zero.

2. Baza și dimensiunea. Definiție. Sistem de vectori liniar independenți se numește spațiu vectorial bază acest spațiu, dacă orice vector din poate fi reprezentat ca o combinație liniară a vectorilor acestui sistem, adică. pentru fiecare vector există numere reale astfel încât egalitatea este valabilă.Această egalitate se numește descompunere vectorialăîn funcție de bază și de numere numit coordonate vectoriale relativ la bază(sau în bază) .

Teorema (cu privire la unicitatea expansiunii din punct de vedere al bazei). Fiecare vector spațial poate fi extins din punct de vedere al bazei într-un mod unic, adică coordonatele fiecărui vector din bază sunt definite fără ambiguitate.

Introdus de noi operații liniare pe vectori face posibilă crearea diferitelor expresii pentru cantități vectorialeși transformați-le folosind proprietățile setate pentru aceste operații.

Pe baza unui set dat de vectori a 1 , ... și n , puteți compune o expresie de forma

unde a 1 , ... și n sunt numere reale arbitrare. Această expresie se numește combinație liniară de vectori a 1 , ..., a n . Numerele α i , i = 1, n , sunt coeficienți de combinație liniară. Se mai numește și mulțimea vectorilor sistem vectorial.

În legătură cu conceptul introdus de combinație liniară de vectori, se pune problema descrierii mulțimii de vectori care pot fi scrise ca o combinație liniară a unui sistem dat de vectori a 1 , ..., a n . În plus, întrebările despre condițiile în care există o reprezentare a unui vector sub forma unei combinații liniare și despre unicitatea unei astfel de reprezentări sunt naturale.

Definiție 2.1. Vectorii a 1 , ... și n sunt numiți dependent liniar, dacă există o astfel de mulțime de coeficienți α 1 , ... , α n , că

α 1 a 1 + ... + α n a n = 0 (2.2)

și cel puțin unul dintre acești coeficienți este diferit de zero. Dacă setul specificat de coeficienți nu există, atunci vectorii sunt numiți liniar independent.

Dacă α 1 = ... = α n = 0, atunci, evident, α 1 a 1 + ... + α n a n = 0. Având în vedere acest lucru, putem spune următoarele: vectori a 1 , ..., și n sunt liniar independenți dacă din egalitatea (2.2) rezultă că toți coeficienții α 1 , ... , α n sunt egali cu zero.

Următoarea teoremă explică de ce noul concept este numit termenul „dependență” (sau „independență”) și oferă un criteriu simplu pentru dependența liniară.

Teorema 2.1. Pentru ca vectorii a 1 , ..., și n , n > 1 să fie liniar dependenți, este necesar și suficient ca unul dintre ei să fie o combinație liniară a celorlalți.

◄ Necesitatea. Să presupunem că vectorii a 1 , ... și n sunt dependenți liniar. Conform definiției 2.1 a dependenței liniare, în egalitatea (2.2) există cel puțin un coeficient diferit de zero în stânga, de exemplu α 1 . Lăsând primul termen în partea stângă a egalității, mutăm restul în partea dreaptă, schimbându-le semnele ca de obicei. Împărțind egalitatea rezultată la α 1 , obținem

a 1 =-α 2 /α 1 ⋅ a 2 - ... - α n / α 1 ⋅ a n

acestea. reprezentarea vectorului a 1 ca o combinație liniară a vectorilor rămași a 2 , ... și n .

Adecvarea. Fie, de exemplu, primul vector a 1 poate fi reprezentat ca o combinație liniară a vectorilor rămași: a 1 = β 2 a 2 + ... + β n a n . Transferând toți termenii din partea dreaptă spre stânga, obținem un 1 - β 2 a 2 - ... - β n a n = 0, adică. combinație liniară de vectori a 1 , ... și n cu coeficienți α 1 = 1, α 2 = - β 2 , ..., α n = - β n , egal cu vector zero.În această combinație liniară, nu toți coeficienții sunt egali cu zero. Conform definiției 2.1, vectorii a 1 , ... și n sunt dependenți liniar.

Definiția și criteriul dependenței liniare sunt formulate în așa fel încât să implice prezența a doi sau mai mulți vectori. Totuși, se poate vorbi și despre o dependență liniară a unui vector. Pentru a realiza această posibilitate, în loc de „vectorii sunt dependenți liniar” trebuie să spunem „sistemul de vectori este dependent liniar”. Este ușor de observat că expresia „un sistem de un vector este dependent liniar” înseamnă că acest singur vector este zero (există un singur coeficient într-o combinație liniară și nu trebuie să fie egal cu zero).

Conceptul de dependență liniară are o interpretare geometrică simplă. Această interpretare este clarificată de următoarele trei afirmații.

Teorema 2.2. Doi vectori sunt dependenți liniar dacă și numai dacă coliniare.

◄ Dacă vectorii a și b sunt dependenți liniar, atunci unul dintre ei, de exemplu a, este exprimat prin celălalt, adică. a = λb pentru un număr real λ. Conform definiției 1.7 lucrări vectori printr-un număr, vectorii a și b sunt coliniari.

Acum să fie vectorii a și b coliniari. Dacă ambele sunt zero, atunci este evident că sunt dependente liniar, deoarece orice combinație liniară a acestora este egală cu vectorul zero. Fie ca unul dintre acești vectori să nu fie egal cu 0, de exemplu vectorul b. Notăm cu λ raportul lungimilor vectorilor: λ = |а|/|b|. Vectorii coliniari pot fi unidirecțional sau directii opuse. În acest din urmă caz, schimbăm semnul lui λ. Apoi, verificând Definiția 1.7, vedem că a = λb. Conform teoremei 2.1, vectorii a și b sunt liniar dependenți.

Observație 2.1.În cazul a doi vectori, ținând cont de criteriul dependenței liniare, teorema demonstrată poate fi reformulată astfel: doi vectori sunt coliniari dacă și numai dacă unul dintre ei este reprezentat ca produs al celuilalt printr-un număr. Acesta este un criteriu convenabil pentru coliniaritatea a doi vectori.

Teorema 2.3. Trei vectori sunt dependenți liniar dacă și numai dacă coplanare.

◄ Dacă trei vectori a, b, c sunt liniar dependenți, atunci, conform teoremei 2.1, unul dintre ei, de exemplu a, este o combinație liniară a celorlalți: a = βb + γc. Să combinăm originile vectorilor b și c în punctul A. Atunci vectorii βb, γc vor avea o origine comună în punctul A și paralelogramul își reglează suma, acestea. vector a, va fi un vector cu începutul A și Sfârşit, care este vârful unui paralelogram construit pe vectori sumand. Astfel, toți vectorii se află în același plan, adică sunt coplanari.

Fie vectorii a, b, c coplanari. Dacă unul dintre acești vectori este zero, atunci este evident că va fi o combinație liniară a celorlalți. Este suficient să luăm toți coeficienții combinației liniare egale cu zero. Prin urmare, putem presupune că toți cei trei vectori nu sunt zero. Compatibil start aceşti vectori într-un punct comun O. Fie capetele lor, respectiv, punctele A, B, C (Fig. 2.1). Desenați drepte prin punctul C paralele cu liniile care trec prin perechi de puncte O, A și O, B. Notând punctele de intersecție A" și B", obținem un paralelogram OA"CB", prin urmare, OC" = OA" + OB " . Vector OA" și vectorul diferit de zero a= OA sunt coliniare și, prin urmare, primul dintre ele poate fi obținut prin înmulțirea celui de-al doilea cu un număr real α:OA" = αOA. În mod similar, OB" = βOB , β ∈ R. Ca rezultat, obținem că OC" = α OA + βOB , adică vectorul c este o combinație liniară a vectorilor a și b. Conform teoremei 2.1, vectorii a, b, c sunt liniar dependenți.

Teorema 2.4. Oricare patru vectori sunt dependenți liniar.

◄ Demonstrarea urmează aceeași schemă ca în teorema 2.3. Luați în considerare patru vectori arbitrari a, b, c și d. Dacă unul dintre cei patru vectori este zero, sau există doi vectori coliniari printre ei sau trei dintre cei patru vectori sunt coplanari, atunci acești patru vectori sunt dependenți liniar. De exemplu, dacă vectorii a și b sunt coliniari, atunci putem compune combinația lor liniară αa + βb = 0 cu coeficienți nenuli, apoi adăugați cei doi vectori rămași la această combinație, luând zerouri ca coeficienți. Obținem o combinație liniară de patru vectori egali cu 0, în care există coeficienți nenuli.

Astfel, putem presupune că dintre cei patru vectori aleși nu există nuli, nici doi nu sunt coliniari și nici trei nu sunt coplanari. Alegem ca început comun punctul O. Atunci capetele vectorilor a, b, c, d vor fi niște puncte A, B, C, D (Fig. 2.2). Prin punctul D trasăm trei plane paralele cu planurile ОВС, OCA, OAB, și fie A", B", С" punctele de intersecție ale acestor plane cu dreptele OA, OB, respectiv OS. Obținem un paralelipiped OA"C"B"C" B"DA", iar vectorii a, b, c se află pe marginile sale care ies din vârful O. Deoarece patrulaterul OC"DC" este un paralelogram, atunci OD = OC" + OC ". La rândul său, segmentul OS" este un paralelogram diagonal OA"C"B", deci OC" = OA" + OB" și OD = OA" + OB" + OC" .

Rămâne de observat că perechile de vectori OA ≠ 0 și OA" , OB ≠ 0 și OB" , OC ≠ 0 și OC" sunt coliniari și, prin urmare, putem alege coeficienții α, β, γ astfel încât OA" = αOA, OB" = βOB și OC" = yOC. În cele din urmă, obținem OD = αOA + βOB + γOC . În consecință, vectorul OD este exprimat în termenii celor trei vectori rămași, iar toți cei patru vectori, conform teoremei 2.1, sunt liniar dependenți.

Definiția 1. Un sistem de vectori se numește dependent liniar dacă unul dintre vectorii sistemului poate fi reprezentat ca combinație liniară alți vectori ai sistemului și liniar independenți - în caz contrar.

Definiția 1´. Un sistem de vectori se numește dependent liniar dacă există numere Cu 1 , Cu 2 , …, Cu k , nu toate egale cu zero, astfel încât combinația liniară de vectori cu coeficienți dați este egală cu vectorul zero: = , altfel sistemul se numește liniar independent.

Să arătăm că aceste definiții sunt echivalente.

Fie satisfăcută Definiția 1, adică unul dintre vectorii sistemului este egal cu o combinație liniară a restului:

O combinație liniară a unui sistem de vectori este egală cu un vector zero și nu toți coeficienții acestei combinații sunt egali cu zero, adică. definiția 1’ este valabilă.

Fie satisfăcută Definiția 1´. Combinația liniară a sistemului de vectori este , și nu toți coeficienții combinației sunt egali cu zero, de exemplu, coeficienții vectorului .

Am prezentat unul dintre vectorii sistemului ca o combinație liniară a celorlalți, i.e. definiția 1 este îndeplinită.

Definiția 2. Se numește vectorul unitar sau ort vector n-dimensional , care i A-lea coordonată este egală cu unu, iar restul sunt zero.

. (1, 0, 0, …, 0),

(0, 1, 0, …, 0),

(0, 0, 0, …, 1).

Teorema 1. Diversi vectori unitari n-spaţiile dimensionale sunt liniar independente.

Dovada. Fie combinația liniară a acestor vectori cu coeficienți arbitrari să fie egală cu vectorul zero.

Din această egalitate rezultă că toți coeficienții sunt egali cu zero. Avem o contradicție.

Fiecare vector n-spațiul dimensional ā (A 1 , A 2 , ..., A n ) poate fi reprezentat ca o combinație liniară de vectori unitari cu coeficienți egali cu coordonatele vectorului

Teorema 2. Dacă sistemul de vectori conține un vector zero, atunci acesta este dependent liniar.

Dovada. Fie dat un sistem de vectori și unul dintre vectori să fie zero, de exemplu = . Apoi, cu vectorii acestui sistem, este posibil să se compună o combinație liniară egală cu vectorul zero și nu toți coeficienții vor fi zero:

Prin urmare, sistemul este dependent liniar.

Teorema 3. Dacă un subsistem al unui sistem de vectori este dependent liniar, atunci întregul sistem este dependent liniar.

Dovada. Dat un sistem de vectori . Să presupunem că sistemul este dependent liniar, adică. sunt numere Cu 1 , Cu 2 , …, Cu r , nu toate egale cu zero, astfel încât = . Apoi

S-a dovedit că combinația liniară a vectorilor întregului sistem este egală și nu toți coeficienții acestei combinații sunt egali cu zero. Prin urmare, sistemul de vectori este dependent liniar.

Consecinţă. Dacă un sistem de vectori este independent liniar, atunci oricare dintre subsistemele sale este, de asemenea, independent liniar.

Dovada.

Să presupunem contrariul, adică un anumit subsistem este dependent liniar. Din teoremă rezultă că întregul sistem este dependent liniar. Am ajuns la o contradicție.

Teorema 4 (teorema lui Steinitz). Dacă fiecare dintre vectori este o combinație liniară a vectorilor și m>n, atunci sistemul de vectori este dependent liniar.

Consecinţă.În orice sistem de vectori n -dimensionali, nu pot exista mai mult de n vectori liniar independenți.

Dovada. Fiecare n vectorul -dimensional este exprimat ca o combinație liniară de n vectori unitari. Prin urmare, dacă sistemul conține m vectori şi m>n, apoi, după teoremă, acest sistem este dependent liniar.