Drawings of the inscribed and circumscribed circles. Inscribed and circumscribed circles. Property of the circle to which the vertices of a triangle belong

Let's first understand the difference between a circle and a circle. To see this difference, it is enough to consider what both figures are. This is an infinite number of points in the plane, located at an equal distance from a single central point. But, if the circle also consists of internal space, then it does not belong to the circle. It turns out that a circle is both a circle that bounds it (o-circle (g)ness), and an uncountable number of points that are inside the circle.

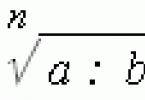
For any point L lying on the circle, the equality OL=R applies. (The length of the segment OL is equal to the radius of the circle).

A line segment that connects two points on a circle is chord.

A chord passing directly through the center of a circle is diameter this circle (D) . The diameter can be calculated using the formula: D=2R

Circumference calculated by the formula: C=2\pi R

Area of a circle: S=\pi R^(2)

arc of a circle called that part of it, which is located between two of its points. These two points define two arcs of a circle. The chord CD subtends two arcs: CMD and CLD. The same chords subtend the same arcs.

Central corner is the angle between two radii.

arc length can be found using the formula:

Using degrees: CD = \frac(\pi R \alpha ^(\circ))(180^(\circ))
Using a radian measure: CD = \alpha R

The diameter that is perpendicular to the chord bisects the chord and the arcs it spans.

If the chords AB and CD of the circle intersect at the point N, then the products of the segments of the chords separated by the point N are equal to each other.

AN\cdot NB = CN \cdot ND

Tangent to circle

Tangent to a circle It is customary to call a straight line that has one common point with a circle.

If a line has two points in common, it is called secant.

If you draw a radius at the point of contact, it will be perpendicular to the tangent to the circle.

Let's draw two tangents from this point to our circle. It turns out that the segments of the tangents will be equal to one another, and the center of the circle will be located on the bisector of the angle with the vertex at this point.

AC=CB

Now we draw a tangent and a secant to the circle from our point. We get that the square of the length of the tangent segment will be equal to the product of the entire secant segment by its outer part.

AC^(2) = CD \cdot BC

We can conclude: the product of an integer segment of the first secant by its outer part is equal to the product of an integer segment of the second secant by its outer part.

AC \cdot BC = EC \cdot DC

Angles in a circle

The degree measures of the central angle and the arc on which it rests are equal.

\angle COD = \cup CD = \alpha ^(\circ)

Inscribed angle is an angle whose vertex is on a circle and whose sides contain chords.

You can calculate it by knowing the size of the arc, since it is equal to half of this arc.

\angle AOB = 2 \angle ADB

Based on diameter, inscribed angle, straight.

\angle CBD = \angle CED = \angle CAD = 90^ (\circ)

Inscribed angles that lean on the same arc are identical.

The inscribed angles based on the same chord are identical or their sum equals 180^ (\circ) .

\angle ADB + \angle AKB = 180^ (\circ)

\angle ADB = \angle AEB = \angle AFB

On the same circle are the vertices of triangles with identical angles and a given base.

An angle with a vertex inside the circle and located between two chords is identical to half the sum of the angular magnitudes of the arcs of the circle that are inside the given and vertical angles.

\angle DMC = \angle ADM + \angle DAM = \frac(1)(2) \left (\cup DmC + \cup AlB \right)

An angle with a vertex outside the circle and located between two secants is identical to half the difference in the angular magnitudes of the arcs of a circle that are inside the angle.

\angle M = \angle CBD - \angle ACB = \frac(1)(2) \left (\cup DmC - \cup AlB \right)

Inscribed circle

Inscribed circle is a circle tangent to the sides of the polygon.

At the point where the bisectors of the angles of the polygon intersect, its center is located.

A circle may not be inscribed in every polygon.

The area of a polygon with an inscribed circle is found by the formula:

S=pr,

p is the semiperimeter of the polygon,

r is the radius of the inscribed circle.

It follows that the radius of the inscribed circle is:

r = \frac(S)(p)

The sums of the lengths of opposite sides will be identical if the circle is inscribed in a convex quadrilateral. And vice versa: a circle is inscribed in a convex quadrilateral if the sums of the lengths of opposite sides in it are identical.

AB+DC=AD+BC

It is possible to inscribe a circle in any of the triangles. Only one single. At the point where the bisectors of the inner angles of the figure intersect, the center of this inscribed circle will lie.

The radius of the inscribed circle is calculated by the formula:

r = \frac(S)(p) ,

where p = \frac(a + b + c)(2)

Circumscribed circle

If a circle passes through every vertex of a polygon, then such a circle is called circumscribed about a polygon.

The center of the circumscribed circle will be at the point of intersection of the perpendicular bisectors of the sides of this figure.

The radius can be found by calculating it as the radius of a circle that is circumscribed about a triangle defined by any 3 vertices of the polygon.

There is the following condition: a circle can be circumscribed around a quadrilateral only if the sum of its opposite angles is equal to 180^( \circ) .

\angle A + \angle C = \angle B + \angle D = 180^ (\circ)

Near any triangle it is possible to describe a circle, and one and only one. The center of such a circle will be located at the point where the perpendicular bisectors of the sides of the triangle intersect.

The radius of the circumscribed circle can be calculated by the formulas:

R = \frac(a)(2 \sin A) = \frac(b)(2 \sin B) = \frac(c)(2 \sin C)

R = \frac(abc)(4S)

a, b, c are the lengths of the sides of the triangle,

S is the area of the triangle.

Ptolemy's theorem

Finally, consider Ptolemy's theorem.

Ptolemy's theorem states that the product of diagonals is identical to the sum of the products of opposite sides of an inscribed quadrilateral.

AC \cdot BD = AB \cdot CD + BC \cdot AD

Your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please read our privacy policy and let us know if you have any questions.

Collection and use of personal information

Personal information refers to data that can be used to identify or contact a specific person.

You may be asked to provide your personal information at any time when you contact us.

The following are some examples of the types of personal information we may collect and how we may use such information.

What personal information we collect:

When you submit an application on the site, we may collect various information, including your name, phone number, email address, etc.

How we use your personal information:

The personal information we collect allows us to contact you and inform you about unique offers, promotions and other events and upcoming events.
From time to time, we may use your personal information to send you important notices and messages.
We may also use personal information for internal purposes, such as conducting audits, data analysis and various research in order to improve the services we provide and provide you with recommendations regarding our services.
If you enter a prize draw, contest or similar incentive, we may use the information you provide to administer such programs.

Disclosure to third parties

We do not disclose information received from you to third parties.

Exceptions:

In the event that it is necessary - in accordance with the law, judicial order, in legal proceedings, and / or based on public requests or requests from state bodies in the territory of the Russian Federation - disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public interest reasons.
In the event of a reorganization, merger or sale, we may transfer the personal information we collect to the relevant third party successor.

Protection of personal information

We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as from unauthorized access, disclosure, alteration and destruction.

Maintaining your privacy at the company level

To ensure that your personal information is secure, we communicate privacy and security practices to our employees and strictly enforce privacy practices.

This article contains the minimum set of information about the circle required to successfully pass the exam in mathematics.

circumference called the set of points located at the same distance from a given point, which is called the center of the circle.

For any point lying on the circle, the equality holds (The length of the segment is equal to the radius of the circle.

A line segment that connects two points on a circle is called chord.

The chord passing through the center of the circle is called diameter circles () .

Circumference:

Area of a circle:

Arc of a circle:

The part of a circle enclosed between two of its points is called arc circles. Two points on a circle define two arcs. The chord subtends two arcs: and . Equal chords subtend equal arcs.

The angle between two radii is called central corner :

To find the length of the arc, we make up the proportion:

a) the angle is given in degrees:

b) the angle is given in radians:

Diameter perpendicular to chord , divides this chord and the arcs that it subtracts in half:

If a chords and circles intersect at a point , then the products of segments of chords into which they are divided by a point are equal to each other:

Tangent to a circle.

A straight line that has one point in common with a circle is called tangent to the circle. A line that has two points in common with a circle is called secant.

The tangent to the circle is perpendicular to the radius drawn to the tangent point.

If two tangents are drawn from a given point to the circle, then tangent segments are equal to each other and the center of the circle lies on the bisector of the angle with the vertex at this point:

If a tangent and a secant are drawn from a given point to the circle, then the square of the length of the tangent segment is equal to the product of the entire secant segment by its outer part :

Consequence: the product of the entire segment of one secant by its outer part is equal to the product of the entire segment of the other secant by its outer part:

Angles in a circle.

The degree measure of a central angle is equal to the degree measure of the arc on which it rests:

An angle whose vertex lies on a circle and whose sides contain chords is called inscribed angle . An inscribed angle is measured by half the arc it intercepts:

∠∠

An inscribed angle based on a diameter is a right angle:

∠∠∠

Inscribed angles subtending the same arc are :

The inscribed angles subtending the same chord are equal or their sum is equal to

∠∠

The vertices of triangles with a given base and equal angles at the vertex lie on the same circle:

Angle between two chords (the angle with the vertex inside the circle) is equal to half the sum of the angular magnitudes of the arcs of the circle enclosed inside the given angle and inside the vertical angle.

∠ ∠∠(⌣ ⌣ )

Angle between two secants (the angle with the vertex outside the circle) is equal to the half-difference of the angular magnitudes of the arcs of the circle enclosed inside the angle.

∠ ∠∠(⌣ ⌣ )

Inscribed circle.

The circle is called inscribed in a polygon if it touches its sides. Center of the inscribed circle lies at the intersection point of the angle bisectors of the polygon.

Not every polygon can be inscribed in a circle.

Area of a polygon containing a circle can be found using the formula

here is the semiperimeter of the polygon, is the radius of the inscribed circle.

From here inscribed circle radius equals

If a circle is inscribed in a convex quadrilateral, then the sums of the lengths of opposite sides are . Conversely, if in a convex quadrilateral the sums of the lengths of opposite sides are equal, then a circle can be inscribed in the quadrilateral:

Any triangle can be inscribed with a circle, and only one. The center of the inscribed circle lies at the intersection point of the bisectors of the interior angles of the triangle.

Inscribed circle radius is equal to . Here

circumscribed circle.

The circle is called circumscribed about a polygon if it passes through all the vertices of the polygon. The center of the circumscribed circle lies at the point of intersection of the perpendicular bisectors of the sides of the polygon. The radius is calculated as the radius of a circle circumscribed about a triangle defined by any three vertices of the given polygon:

A circle can be circumscribed about a quadrilateral if and only if the sum of its opposite angles is equal to .

Near any triangle it is possible to describe a circle, moreover, only one. Its center lies at the point of intersection of the perpendicular bisectors of the sides of the triangle:

Radius of the circumscribed circle calculated by the formulas:

Where is the length of the sides of the triangle, is its area.

Ptolemy's theorem

In an inscribed quadrilateral, the product of the diagonals is equal to the sum of the products of its opposite sides:

Video lesson 2: Circle circumscribing a triangle

Lecture: A circle inscribed in a triangle and a circle circumscribing a triangle

A circle can be circumscribed about some triangles, and a circle can be inscribed into some.

inscribed triangle

If all the vertices of a triangle lie on a circle, then such a triangle is called inscribed.

Pay attention, if some triangle is inscribed in a circle, then all lines that connect the center of the circle with the vertices of the triangle are equal. Moreover, they have a radius value.

There are simple formulas that allow you to determine the sides of a triangle by a known radius of a circle, or vice versa, determine the radius along the sides:

If a regular triangle is inscribed in a circle, then the formulas are simplified. I would like to remind you that a right triangle is called one in which all sides are equal:

The formula for finding the area of a regular triangle if it is inscribed in a circle:

If some triangle is located inside the circle, then there is a rule for placing the center of the circle.

If any acute-angled triangle is inscribed in a circle, then the center of this circle will be located inside the triangle:

If a regular triangle is inscribed in a circle, then the center of the circle will be considered the center of the triangle, as well as the intersection point of its heights.

If a right triangle is inscribed in a circle, then the center of the circle will lie in the middle of the hypotenuse: