In this article, you will find properties of the bisector and median of a triangle that can be useful in solving problems.

Bisectors.

1. The point of intersection of the bisectors of the triangle is the center of the circle inscribed in the triangle.

Proof.

Indeed, the points lying on the bisector of the angle are equidistant from the sides of the angle. Therefore, the intersection point of the bisectors is equidistant from all sides of the triangle, that is, it is the center of the inscribed circle.

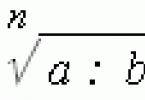
2. The bisector of a triangle divides the opposite side into segments proportional to the adjacent sides:

Proof.

Let's make additional constructions. Draw a line through a point parallel to

Point of intersection of a line and a line:

∠1=∠2, since is the bisector of ∠

∠2=∠3 as lying across, as by construction.

Therefore, ∠1=∠3 and the triangle is isosceles, and .

Consequently,

3. The length of the bisector is calculated by the following formulas:

Let's prove the second formula.

Let us introduce the notation:

Equate the expressions for the area of ​​a triangle:

4. Let O be the center of the inscribed circle, be the angle bisector of the triangle:

Then the relation is fulfilled:

Proof:

Consider a triangle:

Angle bisector, hence by the triangle bisector property

Let then

Let's express . According to the property of the bisector of a triangle:

From here

In some problems it is convenient to extend the bisector of a triangle to the intersection with the circumscribed circle.

The shamrock lemma.

Given a triangle. Point - the point of intersection of the bisector of the angle with the circle circumscribed about the triangle. Let be the center of a circle inscribed in a triangle. Then

Proof.

Inscribed angles that intersect equal arcs are equal. Note the equal inscribed angles:

From here.

The center of the inscribed circle, so is the bisector of the angle.

From a triangle

Then from the triangle

Got .

That is, the triangle is isosceles.

From here.

Proved that

Let us prove formula (1) from item 3:

Proof:

We continue the bisector to the intersection with the circumscribed circle. Consider triangles and . Note the equal angles:

A triangle is similar to a triangle in two angles. From here:

By the property of segments of intersecting chords

Substitute (3) into (2) and use (4):

We express the lengths of the segments into which the bisector divides the side of the triangle in terms of the lengths of the sides of the triangle. Let us introduce the notation:

We get the system:

Medians.

1. The medians of a triangle are divided by the intersection point in a ratio of 2:1, counting from the top:

2. Let be a point inside the triangle such that the relation is fulfilled: , then - the point of intersection of the medians of the triangle.

Proof.

Let us prove an auxiliary theorem.

Lemma.

For an arbitrary point inside the triangle, the following relation holds:

Let us drop from points and perpendiculars to :

From the similarity of triangles we get:

If we consider triangles and with a common base , then we get the ratio:

Similarly, we get

Adding these equalities, we get:

We use this lemma to prove Assertion 2.

If the equality (1) , then the equality (2) and from the lemma it follows that in equality (2) each fraction is equal to .

Let us prove that in this case the segments are medians.

If a , then we get . Let us draw straight lines through the point, parallel to and and consider two pairs of similar triangles: and :

From here we get

From the similarity of triangles we get, that is, the point is the middle of the segment. From here.

Therefore, is the median of the triangle.

3. The medians of a triangle, intersecting, divide it into 6 equal triangles.

Proof.

Let's prove that

because ,

because ,

Consequently,

Heights.

1. The lines containing the altitudes of the triangle intersect at one point. In the case of an acute triangle, the heights themselves intersect at one point.

2. The intersection point of the heights of a triangle has the following property: the sum of the square of the distance from the vertex of the triangle and the square of the opposite side is the same for any vertex:

Proof.

Let's prove the first part of the equality:

Let's rewrite it in the form:

According to the Pythagorean theorem: (from triangles and )

(from triangle)

(from triangle)

Substitute these expressions in (1), we get:

Expanding the brackets, we get:

We got an identity. The second part of the equality is proved similarly.

3. If we describe a circle around the triangle and extend the heights of the triangle to the intersection with this circle,

then for any height of the triangle, the distance from the base of the height to the point of intersection of the continuation of the height with the circle is equal to the distance from the base of the height to the point of intersection of the heights:

Or like this: Points symmetrical to the point of intersection of the altitudes of the triangle with respect to the sides of the triangle lie on the circle circumscribed about the triangle.

Proof.

Let's prove that .

To do this, consider the triangles and , and prove that :

Let's use the sign of equality of triangles on the side and two adjacent angles. - common side. Let us prove the equality of two angles.

Let us prove that ∠ ∠

Let ∠, then from the triangle we get that

∠. Therefore, from the triangle we get that

But ∠ and ∠ are based on the same arc, hence ∠ ∠ ∠

Similarly, we obtain that ∠ ∠

4. In a triangle, the points and are the bases of the heights drawn from the vertices and. Prove that the triangle is similar to the triangle and the similarity coefficient is .

Proof:

The center of a circle circumscribed about a right triangle lies at the midpoint of the hypotenuse . The point lies on this circle, since - hypotenuse of a right triangle:

As inscribed angles based on one arc.

from triangle:

From here. Angle - common angle of triangles and . Therefore, a triangle is similar to a triangle. The similarity coefficient is equal to the ratio of similar sides, that is, sides that lie opposite equal angles:

Ceva's theorem

Let in a triangle

Segments intersect at one point if and only if

Proof.

Let us prove that if the segments intersect at one point, then relation (1) is satisfied.

It is easy to check that if , then

Let's apply this proportion property:

Similarly:

Ceva's theorem can be written as follows:

If the segments intersect at one point, then the relation is fulfilled:

To prove Ceva's theorem in the form of sines, it suffices to substitute the formula for the area of ​​each triangle in the second part of equality (2) instead of the areas of triangles .

From the lectures of Agakhanov Nazar Khangeldyevich and Vladimir Viktorovich Trushkov, CPC MIPT.

Properties

• The medians of a triangle intersect at one point, which is called the centroid, and are divided by this point into two parts in a ratio of 2: 1, counting from the top.
• A triangle is divided by three medians into six triangles of equal area.
• The longer side of the triangle corresponds to the smaller median.
• From the vectors that form the medians, you can make a triangle.
• With affine transformations, the median goes to the median.
• The median of a triangle divides it into two equal parts.

Formulas

• The formula for the median through the sides (derived through the Stewart theorem or by completing it to a parallelogram and using the equality in the parallelogram of the sum of the squares of the sides and the sum of the squares of the diagonals):

, where m c is the median to side c; a, b, c are the sides of a triangle, so the sum of the squares of the medians of an arbitrary triangle is always 4/3 times less than the sum of the squares of its sides.

• Side formula in terms of medians:

, where the medians to the corresponding sides of the triangle are the sides of the triangle.

If two medians are perpendicular, then the sum of the squares of the sides to which they are dropped is 5 times the square of the third side.

Mnemonic rule

median monkey,
who has a keen eye
jump right in the middle
sides against the top,
where is now.

Notes

see also

Links

Wikimedia Foundation. 2010 .

See what the "Median of a triangle" is in other dictionaries:

Median: The median of a triangle in planimetry, the segment connecting the vertex of the triangle with the midpoint of the opposite side in statistics, the median is the population value that divides the ranked data series in half Median (statistics) ... ... Wikipedia

Median: The median of a triangle in planimetry, the segment connecting the vertex of the triangle to the midpoint of the opposite side Median (statistics) quantile 0.5 Median (trace) the middle line of the trace drawn between the right and left ... Wikipedia

Triangle and its medians. The median of a triangle is a segment inside a triangle that connects the vertex of the triangle with the midpoint of the opposite side, as well as a straight line containing this segment. Contents 1 Properties 2 Formulas ... Wikipedia

A line that connects the vertex of a triangle with the midpoint of its base. A complete dictionary of foreign words that have come into use in the Russian language. Popov M., 1907. median (lat. mediana medium) 1) geol. a segment that connects the vertex of a triangle with ... ... Dictionary of foreign words of the Russian language

Median (from the Latin mediana middle) in geometry, a segment connecting one of the vertices of a triangle with the midpoint of the opposite side. Three M. triangles intersect at one point, which is sometimes called the "center of gravity" of the triangle, so ... Great Soviet Encyclopedia

A triangle is a straight line (or its segment inside a triangle) connecting the vertex of the triangle with the midpoint of the opposite side. Three M. triangles intersect at one point, to paradise is called the center of gravity of the triangle, the centroid, or ... ... Mathematical Encyclopedia

- (from lat. mediana middle) a segment connecting the apex of a triangle with the middle of the opposite side ... Big Encyclopedic Dictionary

MEDIAN, medians, women. (lat. mediana, lit. middle). 1. A straight line drawn from the vertex of a triangle to the middle of the opposite side (mat.). 2. In statistics, for a series of many data, a quantity that has the property that the number of data, ... ... Explanatory Dictionary of Ushakov

MEDIAN, s, female In mathematics: a straight line segment that connects the vertex of a triangle to the midpoint of the opposite side. Explanatory dictionary of Ozhegov. S.I. Ozhegov, N.Yu. Shvedova. 1949 1992 ... Explanatory dictionary of Ozhegov

MEDIAN (from lat. mediana middle), a segment connecting the apex of a triangle with the middle of the opposite side ... encyclopedic Dictionary

chord properties

1. The diameter (radius), perpendicular to the chord, divides this chord and both arcs contracted by it in half. The converse theorem is also true: if the diameter (radius) bisects a chord, then it is perpendicular to this chord.

2. Arcs enclosed between parallel chords are equal.

3. If two chords of a circle, AB and CD intersect at a point M, then the product of the segments of one chord is equal to the product of the segments of the other chord: AM MB = CM MD.

Circle properties

1. A straight line may not have common points with a circle; have one common point with the circle ( tangent); have two common points with it ( secant).

2. Through three points that do not lie on one straight line, it is possible to draw a circle, and moreover, only one.

3. The point of contact of two circles lies on the line connecting their centers.

Tangent and secant theorem

If a tangent and a secant are drawn from a point lying outside the circle, then the square of the length of the tangent is equal to the product of the secant by its outer part: MC 2 = MA MB.

The secant theorem

If two secants are drawn from a point lying outside the circle, then the product of one secant by its outer part is equal to the product of the other secant by its outer part. MA MB = MC MD.

Angles in a circle

Central An angle in a circle is a flat angle with a vertex at its center.

An angle whose vertex lies on a circle and whose sides intersect the circle is called inscribed angle.

Any two points on the circle divide it into two parts. Each of these parts is called arc circles. The measure of an arc can be the measure of its corresponding central angle.

The arc is called semicircle, if the segment connecting its ends is a diameter.

Properties of corners associated with a circle

1. An inscribed angle is either equal to half of its corresponding central angle, or complements half of this angle to 180°.

2. Angles inscribed in one circle and based on the same arc are equal.

3. The inscribed angle based on the diameter is 90°.

5. The angle formed by the tangent to the circle and the secant drawn through the tangent point is equal to half the arc enclosed between its sides.

Lengths and areas

1. Circumference C radius R calculated by the formula: C= 2 R.

2. Area S circle radius R calculated by the formula: S = R2.

3. The length of the arc of a circle L radius R with a central angle, measured in radians, is calculated by the formula: L=R .

4. Square S radius sectors R with a central angle in radians is calculated by the formula: S = R2 .

Inscribed and circumscribed circles

Circle and triangle

the center of the inscribed circle is the point of intersection of the bisectors of the triangle, its radius r calculated by the formula:

r=, where S is the area of ​​the triangle, and - semi-perimeter;

the center of the circumscribed circle is the point of intersection of the medial perpendiculars, its radius R is calculated by the formula:

R= , R = ;

The center of a circle circumscribed about a right-angled triangle lies at the middle of the hypotenuse;

The center of the circumscribed and inscribed circles of a triangle coincide only if this triangle is regular.

Circle and quadrilaterals

A circle can be circumscribed about a convex quadrilateral if and only if the sum of its interior opposite angles is 180°:

180°;

a circle can be inscribed in a quadrilateral if and only if the sums of opposite sides are equal a + c = b + d;

a circle can be circumscribed about a parallelogram if and only if it is a rectangle;

· about a trapezoid it is possible to describe a circle if and only if this trapezoid is isosceles; the center of the circle lies at the intersection of the axis of symmetry of the trapezium with the median perpendicular to the lateral side;

A circle can be inscribed in a parallelogram if and only if it is a rhombus.

triangles

Triangle median properties

1. The median divides the triangle into two triangles of the same area.

2. The medians of a triangle intersect at one point, which divides each of them in a ratio of 2:1, counting from the top. This point is called center of gravity triangle.

3. The whole triangle is divided by its medians into six equal triangles.

Triangle bisector properties

1. The bisector of an angle is the locus of points equidistant from the sides of this angle.

2. The bisector of the interior angle of a triangle divides the opposite side into segments proportional to the adjacent sides: .

3. The point of intersection of the bisectors of a triangle is the center of a circle inscribed in this triangle.

Triangle height properties

1. In a right triangle, the height drawn from the vertex of the right angle divides it into two triangles similar to the original one.

2. In an acute triangle, its two heights cut off similar triangles from it.

There is a theory that the medians of a triangle intersect at one point, and that point divides each median in a ratio of 2:1, where 2 corresponds to the segment from the vertex from which the median is drawn to the point of intersection of the medians, and 1 corresponds to the segment from the point of intersection of the medians to the middle of the side to which the median is drawn.

To prove this theorem, consider a triangle ABC with medians AE, BF, CD. That is, points D, E, F bisect the sides AB, BC, CA, respectively.
We do not know if all medians intersect at one point (this still needs to be proven). However, any two medians will intersect at one point, since they cannot be parallel. Let the medians AE and BF intersect at point O.

The median BF divides the median AE into two segments AO and EO. Let us draw a line through the point E parallel to BF. This line will intersect side AC at some point L. We also draw another line parallel to BF through the midpoint of segment AB (point D). It will intersect AC at point K.

According to the Thales theorem, if successively equal segments are set aside from its vertex on one side of the angle and parallel lines are drawn through the ends of these segments, crossing the other side of the angle, then these parallel lines will cut off segments equal to each other on the second side of the angle.

Let's look at the angle BCA of this triangle. Segments BE and EC are equal to each other, lines BF and EL are parallel to each other. Then, according to the Thales theorem, CL = LF.
But if we look at the angle BAC, since AD ​​= BD and DK || BF, then AK = KF.

Since the segments AF and CF are equal to each other (because they are formed by the median) and each of them is divided into two equal segments, then all four segments of the side AC are equal to each other: AK = KF = FL = LC.

Consider the angle EAC. Parallel straight lines are drawn through the ends of three equal segments of side AC. Consequently, they cut off segments equal to each other on the side AE. The segment AO contains two such segments, and EO only one. Thus, we have proved that at least one median of a triangle is divided by the point of intersection with another median into two segments, the lengths of which are related as 2: 1.

Now consider the intersection of median AE with median CD. Let them intersect at point P.

Similarly to the previous one, it is proved that the parallel lines FM, CD, EN divide the side AB into equal segments. In turn, they also divide AE ​​into three equal segments. Moreover, from the vertex A to the intersection of the medians there are two such segments, and after - one.

One and the same segment cannot be divided into three equal parts so that with one option of division they are of the same size, and with another - of another. Therefore, the points O and P must coincide. This means that all three medians of the triangle intersect at one point.

To prove that the other two medians share the intersection point in a ratio of 2: 1, we can draw parallel lines to the sides AB and BC in the same way as the previous one.

The median is one of the main lines of a triangle. This segment and the line on which it lies connect the point at the head of the corner of the triangle with the midpoint of the opposite side of the same figure. In an equilateral triangle, the median is also the bisector and height.

The property of the median, which will greatly facilitate the solution of many problems, is as follows: if you draw medians from each corner in a triangle, then all of them, intersecting at one point, will be divided in a ratio of 2: 1. The ratio should be counted from the top of the corner.

The median has the property of dividing everything equally. For example, any median divides a triangle into two others, equal in area. And if you draw all three medians, then in a large triangle you get 6 small ones, also equal in area. Such figures (with the same area) are called equal.

Bisector

A bisector is a ray that starts at the vertex of an angle and bisects the same angle. Points lying on a given ray are equidistant from the sides of the angle. The properties of the bisector are a good help in solving problems related to triangles.

In a triangle, a bisector is a segment that lies on the ray of the angle bisector and connects the vertex to the opposite side. The point of intersection with the side divides it into segments, the ratio of which is equal to the ratio of the sides adjacent to them.

If a circle is inscribed in a triangle, then its center will coincide with the intersection point of all the bisectors of this triangle. This property is also reflected in stereometry - there the pyramid plays the role of a triangle, and the ball plays the role of a circle.

Height

Just like the median and the bisector, the height in a triangle primarily connects the vertex of the angle and the opposite side. This connection results in the following: height is a perpendicular drawn from a vertex to a line that contains the opposite side.

If the height is drawn in a right triangle, then, touching the opposite side, it divides the whole triangle into two others, which in turn are similar to the first.

Often the concept of a perpendicular is used in stereometry to determine the relative positions of lines in different planes and the distance between them. In this case, the segment that performs the function of a perpendicular must have a right angle with both lines. Then the numerical value of this segment will show the distance between the two figures.