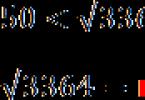Quite often, when solving problems, we are faced with large numbers from which we need to extract Square root. Many students decide that this is a mistake and start resolving the whole example. Under no circumstances should this be done! There are two reasons for this:
- The roots of large numbers do occur in problems. Especially in text;
- There is an algorithm by which these roots are considered almost verbally.
We will consider this algorithm today. Perhaps some things will seem incomprehensible to you. But if you pay attention to this lesson, you will get the most powerful weapon against square roots.
So the algorithm:
- Limit the desired root above and below to multiples of 10. Thus, we will reduce the search range to 10 numbers;
- From these 10 numbers, weed out those that definitely cannot be roots. As a result, 1-2 numbers will remain;
- Square these 1-2 numbers. That of them, the square of which is equal to the original number, will be the root.
Before applying this algorithm works in practice, let's look at each individual step.
Roots constraint
First of all, we need to find out between which numbers our root is located. It is highly desirable that the numbers be a multiple of ten:
10 2 = 100;
20 2 = 400;
30 2 = 900;
40 2 = 1600;
...
90 2 = 8100;
100 2 = 10 000.
We get a series of numbers:
100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.
What do these numbers give us? It's simple: we get boundaries. Take, for example, the number 1296. It lies between 900 and 1600. Therefore, its root cannot be less than 30 and greater than 40:
[Figure caption]
The same is with any other number from which you can find the square root. For example, 3364:
[Figure caption]Thus, instead of an incomprehensible number, we get a very specific range in which the original root lies. To further narrow the scope of the search, go to the second step.
Elimination of obviously superfluous numbers
So, we have 10 numbers - candidates for the root. We received them very quickly, without complex thinking and multiplication in a column. It's time to move on.
Believe it or not, now we will reduce the number of candidate numbers to two - and again without any complicated calculations! It is enough to know the special rule. Here it is:
The last digit of the square depends only on the last digit original number.
In other words, it is enough to look at the last digit of the square - and we will immediately understand where the original number ends.
There are only 10 digits that can be in last place. Let's try to find out what they turn into when they are squared. Take a look at the table:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 | 0 |
This table is another step towards calculating the root. As you can see, the numbers in the second line turned out to be symmetrical with respect to the five. For example:
2 2 = 4;
8 2 = 64 → 4.
As you can see, the last digit is the same in both cases. And this means that, for example, the root of 3364 necessarily ends in 2 or 8. On the other hand, we remember the restriction from the previous paragraph. We get:
[Figure caption] The red squares show that we don't know this figure yet. But after all, the root lies between 50 and 60, on which there are only two numbers ending in 2 and 8:
[Figure caption]That's all! Of all the possible roots, we left only two options! And this is in the most difficult case, because the last digit can be 5 or 0. And then the only candidate for the roots will remain!
Final Calculations
So, we have 2 candidate numbers left. How do you know which one is the root? The answer is obvious: square both numbers. The one that squared will give the original number, and will be the root.
For example, for the number 3364, we found two candidate numbers: 52 and 58. Let's square them:
52 2 \u003d (50 +2) 2 \u003d 2500 + 2 50 2 + 4 \u003d 2704;
58 2 \u003d (60 - 2) 2 \u003d 3600 - 2 60 2 + 4 \u003d 3364.
That's all! It turned out that the root is 58! At the same time, in order to simplify the calculations, I used the formula of the squares of the sum and difference. Thanks to this, you didn’t even have to multiply the numbers in a column! This is another level of optimization of calculations, but, of course, it is completely optional :)
Root Calculation Examples
Theory is good, of course. But let's test it in practice.
[Figure caption]
First, let's find out between which numbers the number 576 lies:
400 < 576 < 900
20 2 < 576 < 30 2
Now let's look at the last number. It is equal to 6. When does this happen? Only if the root ends in 4 or 6. We get two numbers:
It remains to square each number and compare with the original:
24 2 = (20 + 4) 2 = 576
Excellent! The first square turned out to be equal to the original number. So this is the root.
A task. Calculate the square root:
[Figure caption]
900 < 1369 < 1600;
30 2 < 1369 < 40 2;
Let's look at the last number:
1369 → 9;
33; 37.
Let's square it:
33 2 \u003d (30 + 3) 2 \u003d 900 + 2 30 3 + 9 \u003d 1089 ≠ 1369;
37 2 \u003d (40 - 3) 2 \u003d 1600 - 2 40 3 + 9 \u003d 1369.
Here is the answer: 37.
A task. Calculate the square root:
[Figure caption]
We limit the number:
2500 < 2704 < 3600;
50 2 < 2704 < 60 2;
Let's look at the last number:
2704 → 4;
52; 58.
Let's square it:
52 2 = (50 + 2) 2 = 2500 + 2 50 2 + 4 = 2704;
We got the answer: 52. The second number will no longer need to be squared.
A task. Calculate the square root:
[Figure caption]
We limit the number:
3600 < 4225 < 4900;
60 2 < 4225 < 70 2;
Let's look at the last number:
4225 → 5;
65.
As you can see, after the second step, only one option remains: 65. This is the desired root. But let's still square it and check:
65 2 = (60 + 5) 2 = 3600 + 2 60 5 + 25 = 4225;
Everything is correct. We write down the answer.
Conclusion
Alas, no better. Let's take a look at the reasons. There are two of them:
- It is forbidden to use calculators at any normal math exam, be it the GIA or the Unified State Examination. And for carrying a calculator into the classroom, they can easily be kicked out of the exam.
- Don't be like stupid Americans. Which are not like roots - they cannot add two prime numbers. And at the sight of fractions, they generally get hysterical.
Operations with powers and roots. Degree with negative ,
zero and fractional indicator. About expressions that don't make sense.
Operations with degrees.
1. When multiplying powers with the same base, their indicators are added:
a m · a n = a m + n .
2. When dividing degrees with the same base, their indicators subtracted .
3. The degree of the product of two or more factors is equal to the product of the degrees of these factors.
(abc… ) n = a n· b n · c n…
4. The degree of the ratio (fraction) is equal to the ratio of the degrees of the dividend (numerator) and divisor (denominator):
(a/b ) n = a n / b n .
5. When raising a degree to a power, their indicators are multiplied:
(a m ) n = a m n .
All of the above formulas are read and executed in both directions from left to right and vice versa.
EXAMPLE (2 · 3 · 5 / 15)² = 2² 3² 5² / 15² = 900 / 225 = 4 .
Operations with roots. In all the formulas below, the symbol means arithmetic root(radical expression is positive).
1. The root of the product of several factors is equal to the product roots of these factors:
2. The root of the ratio is equal to the ratio of the roots of the dividend and divisor:
3. When raising a root to a power, it is enough to raise to this power root number:
4. If we increase the degree of the root in m once and simultaneously raise to m th power is a root number, then the value of the root will not change:
5. If we decrease the degree of the root in m extract the root once and at the same time m th degree from the radical number, then the value of the root is not will change:
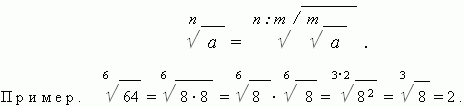
Extension of the concept of degree. So far, we have considered degrees only with a natural indicator; but the actions degrees and roots can also lead to negative, zero and fractional indicators. All these exponents require an additional definition.
Degree with a negative exponent. Power of some number with negative (whole) indicator is defined as a unit divided by to the power of the same number with an exponent equal to the absolute valuenegative indicator:
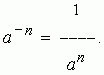
T now formula a m: a n= a m - n can be used not only form, more than n, but also at m, less than n .
EXAMPLE a 4 :a 7 = a 4 - 7 = a - 3 .
If we want the formulaa m : a n= a m - nwas fair atm = n, we need a definition of degree zero.
Degree with zero exponent. The degree of any non-zero number with zero exponent is 1.
EXAMPLES. 2 0 = 1, ( – 5) 0 = 1, (– 3 / 5) 0 = 1.
A degree with a fractional exponent. To raise a real number and to the power m / n , you need to extract the root nth power out of m th power of this number a :
About expressions that don't make sense. There are several such expressions. any number.
Indeed, if we assume that this expression is equal to some number x, then according to the definition of the division operation we have: 0 = 0 x. But this equality holds for any number x, which was to be proved.
Case 3
0 0 - any number.
Really,
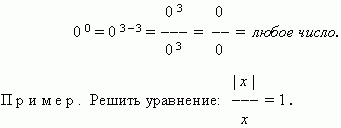
Solution. Consider three main cases:
1) x = 0 – this value does not satisfy this equation
(Why?).
2) when x> 0 we get: x / x = 1, i.e. 1 = 1, whence follows,
what x- any number; but taking into account that
Our case x> 0 , the answer isx > 0 ;
3) when x < 0 получаем: – x / x= 1, i.e. e . –1 = 1, therefore,
In this case, there is no solution.
In this way, x > 0.
At the beginning of the lesson, we will review the basic properties of square roots, and then we will look at some complex examples of simplifying expressions containing square roots.
Topic:Function. Square root properties
Lesson:Converting and simplifying more complex expressions with roots
1. Repetition of the properties of square roots
Let us briefly repeat the theory and recall the main properties of square roots.
Properties of square roots:
1. , therefore, ;
3. 
;
4. 
.
2. Examples for simplifying expressions with roots
Let's move on to examples of using these properties.
Example 1: Simplify an expression 
.
Solution. To simplify, the number 120 must be decomposed into prime factors:
We will open the square of the sum according to the corresponding formula:
Example 2: Simplify an expression 
.
Solution. We take into account that this expression does not make sense for all possible values of the variable, since this expression contains square roots and fractions, which leads to a “narrowing” of the range of acceptable values. ODZ: 
().
We bring the expression in brackets to a common denominator and write the numerator of the last fraction as the difference of squares:
At.
Answer. at.
Example 3: Simplify an expression 
.
Solution. It can be seen that the second bracket of the numerator has an awkward form and needs to be simplified, let's try to factor it using the grouping method.
To be able to take out the common factor, we simplified the roots by factoring them. Substitute the resulting expression into the original fraction:
After reducing the fraction, we apply the difference of squares formula.
3. An example of getting rid of irrationality
Example 4. Get rid of irrationality (roots) in the denominator: a) ; b) .
Solution. a) In order to get rid of irrationality in the denominator, the standard method of multiplying both the numerator and denominator of a fraction by the conjugate factor to the denominator is used (the same expression, but with the opposite sign). This is done to complement the denominator of the fraction to the difference of squares, which allows you to get rid of the roots in the denominator. Let's do this in our case:
b) perform similar actions:
Answer.; .
4. An example for the proof and for the selection of a complete square in a complex radical
Example 5. Prove the equality 
.
Proof. Let's use the definition of the square root, from which it follows that the square of the right expression must be equal to the root expression:
. Let's open the brackets according to the formula of the square of the sum:
, we get the correct equation.
Proven.
Example 6. Simplify the expression.
Solution. This expression is commonly called a complex radical (root under the root). In this example, you need to guess to select the full square from the radical expression. To do this, we note that of the two terms it is a contender for the role of a double product in the formula for the square of the difference (difference, since there is a minus). Let's write it in the form of such a product: , then , claims to be one of the terms of the full square, and 1 to play the role of the second.
Let's substitute this expression under the root.
Converting expressions with roots and powers often requires jumping from roots to powers and vice versa. In this article, we will analyze how such transitions are carried out, what underlies them, and at what points errors most often occur. We will provide all this with characteristic examples with a detailed analysis of the solutions.
Page navigation.
Transition from powers with fractional exponents to roots
The possibility of moving from a degree with a fractional exponent to a root is dictated by the very definition of the degree. Recall how it is determined: the degree of a positive number a with a fractional exponent m / n, where m is an integer, and n is a natural number, is called the n-th root of a m , that is, where a>0, m∈Z, n∈ N. The fractional power of zero is defined similarly 
, with the only difference that in this case m is already considered not an integer, but natural, so that division by zero does not occur.
Thus, the degree can always be replaced by the root. For example, you can go from to , and the degree can be replaced by the root. But you should not move from the expression to the root, since the degree initially does not make sense (the degree of negative numbers is not defined), despite the fact that the root makes sense.
As you can see, there is absolutely nothing tricky in the transition from powers of numbers to roots. Similarly, the transition to the roots of powers with fractional exponents, based on arbitrary expressions, is carried out. Note that the indicated transition is carried out on the ODZ of variables for the original expression. For example, the expression 
on the entire ODZ variable x for this expression can be replaced by the root 
. And from the degree 
go to root 
, such a replacement takes place for any set of variables x , y and z from the DPV for the original expression.
Replacing Roots with Powers
The reverse replacement is also possible, that is, the replacement of roots by degrees with fractional exponents. It is also based on the equality, which in this case is used from right to left, that is, in the form.
For positive a, this transition is obvious. For example, you can replace the degree, and from the root go to the degree with a fractional indicator of the form.
And for negative a, equality does not make sense, but the root may make sense. For example, roots make sense, but they cannot be replaced by powers. So can they be converted to power expressions at all? It is possible if we carry out preliminary transformations, which consist in the transition to roots with non-negative numbers below them, which are then replaced by degrees with fractional exponents. Let us show what these preliminary transformations are and how to carry them out.
In the case of the root, you can perform the following transformations: 
. And since 4 is a positive number, the last root can be replaced by a power. And in the second case determining the root of an odd degree from a negative number−a (in this case, a is positive), which is expressed by the equality 
, allows the root to be replaced by an expression in which the cube root of two can already be replaced by a degree, and it will take the form .
It remains to figure out how the roots, under which the expressions are located, are replaced by the degrees containing these expressions at the base. Here you should not rush to replace with, we denoted by the letter A some expression. Let's take an example to clarify what this means. One wants to replace the root with a degree, based on equality. But such a replacement is appropriate only if x−3≥0<0 ) она не подходит, так как формула не имеет смысла для отрицательных a . Если обратить внимание на ОДЗ, то несложно заметить ее сужение при переходе от выражения к выражению , а помните, что мы договорились не прибегать к преобразованиям, сужающим ОДЗ.
Due to such inaccurate application of the formula, errors often occur when moving from roots to powers. For example, in the textbook, the task is given to present the expression as a degree with a rational exponent, and the answer is given, which raises questions, since the constraint b>0 is not set in the condition. And in the textbook there is a transition from the expression 
, most likely through the following transformations of the irrational expression 
to the expression. The last transition also raises questions, as it narrows the ODZ.
A logical question arises: “How is it correct to move from the root to the degree for all values of variables from the ODZ”? This replacement is based on the following assertions:
Before substantiating the recorded results, we give several examples of their use to move from roots to powers. First, let's go back to the expression. It had to be replaced not by , but by (in this case, m=2 is an even integer, n=3 is a natural number). Another example: 
.
Now the promised substantiation of the results.
When m is an odd integer, and n is a positive integer, then for any set of variables from the DPV for the expression, the value of the expression A is positive (if m<0 ) или неотрицательно (если m>0 ). That's why, .
Let's move on to the second result. Let m be a positive odd integer and n an odd natural number. For all values of variables from the ODZ for which the value of the expression A is non-negative, 
, and for which it is negative, 
The following result is proved similarly for negative and odd integers m and natural odd n . For all values of variables from the ODZ for which the value of the expression A is positive, , and for which it is negative,
Finally, the last result. Let m be an even integer, n any natural number. For all values of variables from the ODZ for which the value of the expression A is positive (if m<0
) или неотрицательно (если m>0
), . And for which it is negative, . Thus, if m is an even integer, n is any natural number, then for any set of values of variables from the DPV for expression it can be replaced by .
Bibliography.
- Algebra and the beginning of the analysis: Proc. for 10-11 cells. general education institutions / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn and others; Ed. A. N. Kolmogorova.- 14th ed.- M.: Enlightenment, 2004.- 384 p.: ill.- ISBN 5-09-013651-3.
- Algebra and the beginning of mathematical analysis. Grade 11: textbook. for general education institutions: basic and profile. levels / [Yu. M. Kolyagin, M. V. Tkacheva, N. E. Fedorova, M. I. Shabunin]; ed. A. B. Zhizhchenko. - M .: Education, 2009. - 336 p.: Ill. - ISBN 979-5-09-016551-8.
Congratulations: today we will analyze the roots - one of the most mind-blowing topics of the 8th grade. :)
Many people get confused about the roots not because they are complex (which is complicated - a couple of definitions and a couple more properties), but because in most school textbooks the roots are defined through such wilds that only the authors of the textbooks themselves can understand this scribbling. And even then only with a bottle of good whiskey. :)
Therefore, now I will give the most correct and most competent definition of the root - the only one that you really need to remember. And only then I will explain: why all this is necessary and how to apply it in practice.
But first, remember one important point, which for some reason many compilers of textbooks “forget” about:
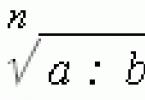
Roots can be of even degree (our favorite $\sqrt(a)$, as well as any $\sqrt(a)$ and even $\sqrt(a)$) and odd degree (any $\sqrt(a)$, $\ sqrt(a)$ etc.). And the definition of the root of an odd degree is somewhat different from the even one.
Here in this fucking “somewhat different” is hidden, probably, 95% of all errors and misunderstandings associated with the roots. So let's clear up the terminology once and for all:
Definition. Even root n from the number $a$ is any non-negative a number $b$ such that $((b)^(n))=a$. And the root of an odd degree from the same number $a$ is generally any number $b$ for which the same equality holds: $((b)^(n))=a$.
In any case, the root is denoted like this:
\(a)\]
The number $n$ in such a notation is called the root exponent, and the number $a$ is called the radical expression. In particular, for $n=2$ we get our “favorite” square root (by the way, this is a root of an even degree), and for $n=3$ we get a cubic root (an odd degree), which is also often found in problems and equations.
Examples. Classic examples of square roots:
\[\begin(align) & \sqrt(4)=2; \\ & \sqrt(81)=9; \\ & \sqrt(256)=16. \\ \end(align)\]
By the way, $\sqrt(0)=0$ and $\sqrt(1)=1$. This is quite logical since $((0)^(2))=0$ and $((1)^(2))=1$.
Cubic roots are also common - do not be afraid of them:
\[\begin(align) & \sqrt(27)=3; \\ & \sqrt(-64)=-4; \\ & \sqrt(343)=7. \\ \end(align)\]
Well, a couple of "exotic examples":
\[\begin(align) & \sqrt(81)=3; \\ & \sqrt(-32)=-2. \\ \end(align)\]
If you do not understand what is the difference between an even and an odd degree, reread the definition again. It is very important!
In the meantime, we will consider one unpleasant feature of the roots, because of which we needed to introduce a separate definition for even and odd exponents.
Why do we need roots at all?
After reading the definition, many students will ask: “What did mathematicians smoke when they came up with this?” And really: why do we need all these roots?
To answer this question, let's go back to elementary school for a moment. Remember: in those distant times, when the trees were greener and the dumplings were tastier, our main concern was to multiply the numbers correctly. Well, something in the spirit of "five by five - twenty-five", that's all. But after all, you can multiply numbers not in pairs, but in triplets, fours, and generally whole sets:
\[\begin(align) & 5\cdot 5=25; \\ & 5\cdot 5\cdot 5=125; \\ & 5\cdot 5\cdot 5\cdot 5=625; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5=3125; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5=15\ 625. \end(align)\]
However, this is not the point. The trick is different: mathematicians are lazy people, so they had to write down the multiplication of ten fives like this:
So they came up with degrees. Why not write the number of factors as a superscript instead of a long string? Like this one:
It's very convenient! All calculations are reduced by several times, and you can not spend a bunch of parchment sheets of notebooks to write down some 5 183 . Such an entry was called the degree of a number, a bunch of properties were found in it, but happiness turned out to be short-lived.
After a grandiose booze, which was organized just about the “discovery” of degrees, some especially stoned mathematician suddenly asked: “What if we know the degree of a number, but we don’t know the number itself?” Indeed, if we know that a certain number $b$, for example, gives 243 to the 5th power, then how can we guess what the number $b$ itself is equal to?
This problem turned out to be much more global than it might seem at first glance. Because it turned out that for the majority of “ready-made” degrees there are no such “initial” numbers. Judge for yourself:
\[\begin(align) & ((b)^(3))=27\Rightarrow b=3\cdot 3\cdot 3\Rightarrow b=3; \\ & ((b)^(3))=64\Rightarrow b=4\cdot 4\cdot 4\Rightarrow b=4. \\ \end(align)\]
What if $((b)^(3))=50$? It turns out that you need to find a certain number, which, when multiplied by itself three times, will give us 50. But what is this number? It is clearly greater than 3 because 3 3 = 27< 50. С тем же успехом оно меньше 4, поскольку 4 3 = 64 >50. I.e. this number lies somewhere between three and four, but what it is equal to - FIG you will understand.
This is exactly why mathematicians came up with $n$-th roots. That is why the radical icon $\sqrt(*)$ was introduced. To denote the same number $b$, which, to the specified power, will give us a previously known value
\[\sqrt[n](a)=b\Rightarrow ((b)^(n))=a\]
I do not argue: often these roots are easily considered - we saw several such examples above. But still, in most cases, if you think of an arbitrary number, and then try to extract the root of an arbitrary degree from it, you are in for a cruel bummer.
What is there! Even the simplest and most familiar $\sqrt(2)$ cannot be represented in our usual form - as an integer or a fraction. And if you drive this number into a calculator, you will see this:
\[\sqrt(2)=1.414213562...\]
As you can see, after the decimal point there is an endless sequence of numbers that do not obey any logic. You can, of course, round this number to quickly compare with other numbers. For example:
\[\sqrt(2)=1.4142...\approx 1.4 \lt 1.5\]
Or here's another example:
\[\sqrt(3)=1.73205...\approx 1.7 \gt 1.5\]
But all these roundings are, firstly, rather rough; and secondly, you also need to be able to work with approximate values, otherwise you can catch a bunch of non-obvious errors (by the way, the skill of comparison and rounding is necessarily checked at the profile exam).
Therefore, in serious mathematics, one cannot do without roots - they are the same equal representatives of the set of all real numbers $\mathbb(R)$, like fractions and integers that we have long known.
The impossibility of representing the root as a fraction of the form $\frac(p)(q)$ means that this root is not a rational number. Such numbers are called irrational, and they cannot be accurately represented except with the help of a radical, or other constructions specially designed for this (logarithms, degrees, limits, etc.). But more on that another time.
Consider a few examples where, after all the calculations, irrational numbers will still remain in the answer.
\[\begin(align) & \sqrt(2+\sqrt(27))=\sqrt(2+3)=\sqrt(5)\approx 2,236... \\ & \sqrt(\sqrt(-32 ))=\sqrt(-2)\approx -1,2599... \\ \end(align)\]
Naturally, by the appearance of the root, it is almost impossible to guess which numbers will come after the decimal point. However, it is possible to calculate on a calculator, but even the most advanced date calculator gives us only the first few digits of an irrational number. Therefore, it is much more correct to write the answers as $\sqrt(5)$ and $\sqrt(-2)$.
That's what they were invented for. To make it easy to write down answers.
Why are two definitions needed?
The attentive reader has probably already noticed that all the square roots given in the examples are taken from positive numbers. Well, at least from zero. But cube roots are calmly extracted from absolutely any number - even positive, even negative.
Why is this happening? Take a look at the graph of the function $y=((x)^(2))$:
The graph of a quadratic function gives two roots: positive and negative Let's try to calculate $\sqrt(4)$ using this graph. To do this, a horizontal line $y=4$ (marked in red) is drawn on the graph, which intersects the parabola at two points: $((x)_(1))=2$ and $((x)_(2)) =-2$. This is quite logical, since
Everything is clear with the first number - it is positive, therefore it is the root:
But then what to do with the second point? Does the 4 have two roots at once? After all, if we square the number −2, we also get 4. Why not write $\sqrt(4)=-2$ then? And why do teachers look at such records as if they want to eat you? :)
The trouble is that if no additional conditions are imposed, then the four will have two square roots - positive and negative. And any positive number will also have two of them. But negative numbers will not have roots at all - this can be seen from the same graph, since the parabola never falls below the axis y, i.e. does not take negative values.
A similar problem occurs for all roots with an even exponent:
- Strictly speaking, each positive number will have two roots with an even exponent $n$;
- From negative numbers, the root with even $n$ is not extracted at all.
That is why the definition of an even root $n$ specifically stipulates that the answer must be a non-negative number. This is how we get rid of ambiguity.
But for odd $n$ there is no such problem. To see this, let's take a look at the graph of the function $y=((x)^(3))$:
The cubic parabola takes on any value, so the cube root can be taken from any number Two conclusions can be drawn from this graph:
- The branches of a cubic parabola, unlike the usual one, go to infinity in both directions - both up and down. Therefore, at whatever height we draw a horizontal line, this line will definitely intersect with our graph. Therefore, the cube root can always be taken, absolutely from any number;
- In addition, such an intersection will always be unique, so you don’t need to think about which number to consider the “correct” root, and which one to score. That is why the definition of roots for an odd degree is simpler than for an even one (there is no non-negativity requirement).
It's a pity that these simple things are not explained in most textbooks. Instead, our brains begin to soar with all sorts of arithmetic roots and their properties.
Yes, I do not argue: what is an arithmetic root - you also need to know. And I will talk about this in detail in a separate lesson. Today we will also talk about it, because without it, all reflections on the roots of the $n$-th multiplicity would be incomplete.
But first you need to clearly understand the definition that I gave above. Otherwise, due to the abundance of terms, such a mess will begin in your head that in the end you will not understand anything at all.
And all you need to understand is the difference between even and odd numbers. Therefore, once again we will collect everything that you really need to know about the roots:
- An even root exists only from a non-negative number and is itself always a non-negative number. For negative numbers, such a root is undefined.
- But the root of an odd degree exists from any number and can itself be any number: for positive numbers it is positive, and for negative numbers, as the cap hints, it is negative.
Is it difficult? No, it's not difficult. Clear? Yes, it's obvious! Therefore, now we will practice a little with the calculations.
Basic properties and limitations
Roots have a lot of strange properties and restrictions - this will be a separate lesson. Therefore, now we will consider only the most important "chip", which applies only to roots with an even exponent. We write this property in the form of a formula:
\[\sqrt(((x)^(2n)))=\left| x\right|\]
In other words, if we raise a number to an even power, and then extract the root of the same degree from this, we will get not the original number, but its modulus. This is a simple theorem that is easy to prove (it suffices to consider separately non-negative $x$, and then separately consider negative ones). Teachers constantly talk about it, it is given in every school textbook. But as soon as it comes to solving irrational equations (i.e. equations containing the sign of the radical), the students forget this formula together.
To understand the issue in detail, let's forget all the formulas for a minute and try to count two numbers ahead:
\[\sqrt(((3)^(4)))=?\quad \sqrt(((\left(-3 \right))^(4)))=?\]
These are very simple examples. The first example will be solved by most of the people, but on the second, many stick. To solve any such crap without problems, always consider the procedure:
- First, the number is raised to the fourth power. Well, it's kind of easy. A new number will be obtained, which can even be found in the multiplication table;
- And now from this new number it is necessary to extract the root of the fourth degree. Those. there is no "reduction" of roots and degrees - these are sequential actions.
Let's deal with the first expression: $\sqrt(((3)^(4)))$. Obviously, you first need to calculate the expression under the root:
\[((3)^(4))=3\cdot 3\cdot 3\cdot 3=81\]
Then we extract the fourth root of the number 81:
Now let's do the same with the second expression. First, we raise the number −3 to the fourth power, for which we need to multiply it by itself 4 times:
\[((\left(-3 \right))^(4))=\left(-3 \right)\cdot \left(-3 \right)\cdot \left(-3 \right)\cdot \ left(-3 \right)=81\]
We got a positive number, since the total number of minuses in the product is 4 pieces, and they will all cancel each other out (after all, a minus by a minus gives a plus). Next, extract the root again:
In principle, this line could not be written, since it is a no brainer that the answer will be the same. Those. an even root of the same even power "burns" the minuses, and in this sense the result is indistinguishable from the usual module:
\[\begin(align) & \sqrt(((3)^(4)))=\left| 3\right|=3; \\ & \sqrt(((\left(-3 \right))^(4)))=\left| -3 \right|=3. \\ \end(align)\]
These calculations are in good agreement with the definition of the root of an even degree: the result is always non-negative, and the radical sign is also always a non-negative number. Otherwise, the root is not defined.
Note on the order of operations
- The notation $\sqrt(((a)^(2)))$ means that we first square the number $a$, and then take the square root of the resulting value. Therefore, we can be sure that a non-negative number always sits under the root sign, since $((a)^(2))\ge 0$ anyway;
- But the notation $((\left(\sqrt(a) \right))^(2))$, on the contrary, means that we first extract the root from a certain number $a$ and only then square the result. Therefore, the number $a$ in no case can be negative - this is a mandatory requirement embedded in the definition.
Thus, in no case should one thoughtlessly reduce the roots and degrees, thereby supposedly "simplifying" the original expression. Because if there is a negative number under the root, and its exponent is even, we will get a lot of problems.
However, all these problems are relevant only for even indicators.
Removing a minus sign from under the root sign
Naturally, roots with odd exponents also have their own feature, which, in principle, does not exist for even ones. Namely:
\[\sqrt(-a)=-\sqrt(a)\]
In short, you can take out a minus from under the sign of the roots of an odd degree. This is a very useful property that allows you to "throw" all the minuses out:
\[\begin(align) & \sqrt(-8)=-\sqrt(8)=-2; \\ & \sqrt(-27)\cdot \sqrt(-32)=-\sqrt(27)\cdot \left(-\sqrt(32) \right)= \\ & =\sqrt(27)\cdot \sqrt(32)= \\ & =3\cdot 2=6. \end(align)\]
This simple property greatly simplifies many calculations. Now you don’t need to worry: what if a negative expression got under the root, and the degree at the root turned out to be even? It is enough to “throw out” all the minuses outside the roots, after which they can be multiplied by each other, divided and generally do many suspicious things, which in the case of “classic” roots are guaranteed to lead us to an error.
And here another definition enters the scene - the very one with which most schools begin the study of irrational expressions. And without which our reasoning would be incomplete. Meet!
arithmetic root
Let's assume for a moment that only positive numbers or, in extreme cases, zero can be under the root sign. Let's score on even / odd indicators, score on all the definitions given above - we will work only with non-negative numbers. What then?
And then we get the arithmetic root - it partially intersects with our "standard" definitions, but still differs from them.
Definition. An arithmetic root of the $n$th degree of a non-negative number $a$ is a non-negative number $b$ such that $((b)^(n))=a$.
As you can see, we are no longer interested in parity. Instead, a new restriction appeared: the radical expression is now always non-negative, and the root itself is also non-negative.
To better understand how the arithmetic root differs from the usual one, take a look at the graphs of the square and cubic parabola already familiar to us:
Root search area - non-negative numbers As you can see, from now on, we are only interested in those pieces of graphs that are located in the first coordinate quarter - where the coordinates $x$ and $y$ are positive (or at least zero). You no longer need to look at the indicator to understand whether we have the right to root a negative number or not. Because negative numbers are no longer considered in principle.
You may ask: “Well, why do we need such a castrated definition?” Or: "Why can't we get by with the standard definition given above?"
Well, I will give just one property, because of which the new definition becomes appropriate. For example, the exponentiation rule:
\[\sqrt[n](a)=\sqrt(((a)^(k)))\]
Please note: we can raise the radical expression to any power and at the same time multiply the root exponent by the same power - and the result will be the same number! Here are some examples:
\[\begin(align) & \sqrt(5)=\sqrt(((5)^(2)))=\sqrt(25) \\ & \sqrt(2)=\sqrt(((2)^ (4)))=\sqrt(16) \\ \end(align)\]
Well, what's wrong with that? Why couldn't we do it before? Here's why. Consider a simple expression: $\sqrt(-2)$ is a number that is quite normal in our classical sense, but absolutely unacceptable from the point of view of the arithmetic root. Let's try to convert it:
$\begin(align) & \sqrt(-2)=-\sqrt(2)=-\sqrt(((2)^(2)))=-\sqrt(4) \lt 0; \\ & \sqrt(-2)=\sqrt(((\left(-2 \right))^(2)))=\sqrt(4) \gt 0. \\ \end(align)$
As you can see, in the first case, we took the minus out from under the radical (we have every right, because the indicator is odd), and in the second, we used the above formula. Those. from the point of view of mathematics, everything is done according to the rules.
WTF?! How can the same number be both positive and negative? No way. It's just that the exponentiation formula, which works great for positive numbers and zero, starts to give complete heresy in the case of negative numbers.
Here, in order to get rid of such ambiguity, they came up with arithmetic roots. A separate large lesson is devoted to them, where we consider in detail all their properties. So now we will not dwell on them - the lesson turned out to be too long anyway.
Algebraic root: for those who want to know more
I thought for a long time: to make this topic in a separate paragraph or not. In the end, I decided to leave here. This material is intended for those who want to understand the roots even better - no longer at the average “school” level, but at the level close to the Olympiad.
So: in addition to the "classical" definition of the root of the $n$-th degree from a number and the associated division into even and odd indicators, there is a more "adult" definition, which does not depend on parity and other subtleties at all. This is called an algebraic root.
Definition. An algebraic $n$-th root of any $a$ is the set of all numbers $b$ such that $((b)^(n))=a$. There is no well-established designation for such roots, so just put a dash on top:
\[\overline(\sqrt[n](a))=\left\( b\left| b\in \mathbb(R);((b)^(n))=a \right. \right\) \]
The fundamental difference from the standard definition given at the beginning of the lesson is that the algebraic root is not a specific number, but a set. And since we are working with real numbers, this set is of only three types:
- Empty set. Occurs when it is required to find an algebraic root of an even degree from a negative number;
- A set consisting of a single element. All roots of odd powers, as well as roots of even powers from zero, fall into this category;
- Finally, the set can include two numbers - the same $((x)_(1))$ and $((x)_(2))=-((x)_(1))$ that we saw on the chart quadratic function. Accordingly, such an alignment is possible only when extracting the root of an even degree from a positive number.
The last case deserves more detailed consideration. Let's count a couple of examples to understand the difference.
Example. Compute expressions:
\[\overline(\sqrt(4));\quad \overline(\sqrt(-27));\quad \overline(\sqrt(-16)).\]
Solution. The first expression is simple:
\[\overline(\sqrt(4))=\left\( 2;-2 \right\)\]
It is two numbers that are part of the set. Because each of them squared gives a four.
\[\overline(\sqrt(-27))=\left\( -3 \right\)\]
Here we see a set consisting of only one number. This is quite logical, since the exponent of the root is odd.
Finally, the last expression:
\[\overline(\sqrt(-16))=\varnothing \]
We got an empty set. Because there is not a single real number that, when raised to the fourth (that is, even!) Power, will give us a negative number −16.
Final note. Please note: it was not by chance that I noted everywhere that we are working with real numbers. Because there are also complex numbers - it is quite possible to calculate $\sqrt(-16)$ and many other strange things there.
However, in the modern school curriculum of mathematics, complex numbers are almost never found. They have been omitted from most textbooks because our officials consider the topic "too difficult to understand."
That's all. In the next lesson, we will look at all the key properties of roots and finally learn how to simplify irrational expressions. :)
