Back forward
Attention! The slide preview is for informational purposes only and may not represent the full extent of the presentation. If you are interested in this work, please download the full version.
The purpose of the lesson:
- In a fun way, introduce students to the rule of multiplying a decimal fraction by a natural number, by a bit unit and the rule of expressing a decimal fraction as a percentage. Develop the ability to apply the acquired knowledge in solving examples and problems.
- To develop and activate the logical thinking of students, the ability to identify patterns and generalize them, strengthen memory, the ability to cooperate, provide assistance, evaluate their work and the work of each other.
- To cultivate interest in mathematics, activity, mobility, ability to communicate.
Equipment: interactive board, a poster with a cyphergram, posters with mathematicians' statements.
During the classes
- Organizing time.
- Oral counting is a generalization of previously studied material, preparation for the study of new material.
- Explanation of new material.
- Homework assignment.
- Mathematical physical education.
- Generalization and systematization of the acquired knowledge in a playful way with the help of a computer.
- Grading.
2. Guys, today our lesson will be somewhat unusual, because I will not spend it alone, but with my friend. And my friend is also unusual, now you will see him. (A cartoon computer appears on the screen.) My friend has a name and he can talk. What's your name, friend? Komposha replies: "My name is Komposha." Are you ready to help me today? YES! Well then, let's start the lesson.

Today I received an encrypted cyphergram, guys, which we must solve and decipher together. (A poster is posted on the board with an oral account for adding and subtracting decimal fractions, as a result of which the guys get the following code 523914687. )
| 5 | 2 | 3 | 9 | 1 | 4 | 6 | 8 | 7 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Komposha helps to decipher the received code. As a result of decoding, the word MULTIPLICATION is obtained. Multiplication is the keyword of the topic of today's lesson. The topic of the lesson is displayed on the monitor: “Multiplying a decimal fraction by a natural number”
Guys, we know how the multiplication of natural numbers is performed. Today we will consider the multiplication of decimal numbers by a natural number. The multiplication of a decimal fraction by a natural number can be considered as the sum of terms, each of which is equal to this decimal fraction, and the number of terms is equal to this natural number. For example: 5.21 3 \u003d 5.21 + 5, 21 + 5.21 \u003d 15.63 So 5.21 3 = 15.63. Representing 5.21 as an ordinary fraction of a natural number, we get
And in this case, we got the same result of 15.63. Now, ignoring the comma, let's take the number 521 instead of the number 5.21 and multiply by the given natural number. Here we must remember that in one of the factors the comma is moved two places to the right. When multiplying the numbers 5, 21 and 3, we get a product equal to 15.63. Now, in this example, we will move the comma to the left by two digits. Thus, by how many times one of the factors was increased, the product was reduced by so many times. Based on the similar points of these methods, we draw a conclusion.

To multiply a decimal by a natural number, you need:
1) ignoring the comma, perform the multiplication of natural numbers;
2) in the resulting product, separate with a comma on the right as many characters as there are in a decimal fraction.
The following examples are displayed on the monitor, which we analyze together with Komposha and the guys: 5.21 3 = 15.63 and 7.624 15 = 114.34. After I show multiplication by a round number 12.6 50 \u003d 630. Next, I turn to the multiplication of a decimal fraction by a bit unit. Showing the following examples: 7,423 100 \u003d 742.3 and 5.2 1000 \u003d 5200. So, I introduce the rule for multiplying a decimal fraction by a bit unit:

To multiply a decimal fraction by bit units 10, 100, 1000, etc., it is necessary to move the comma to the right in this fraction by as many digits as there are zeros in the bit unit record.
I end the explanation with the expression of a decimal fraction as a percentage. I enter the rule:

To express a decimal as a percentage, multiply it by 100 and add the % sign.
I give an example on a computer 0.5 100 \u003d 50 or 0.5 \u003d 50%.
4. At the end of the explanation, I give the guys homework, which is also displayed on the computer monitor: № 1030, № 1034, № 1032.

5. In order for the guys to rest a little, to consolidate the topic, we do a mathematical physical education session together with Komposha. Everyone stands up, shows the class the solved examples and they must answer whether the example is correct or incorrect. If the example is solved correctly, then they raise their hands above their heads and clap their palms. If the example is not solved correctly, the guys stretch their arms to the sides and knead their fingers.

6. And now you have a little rest, you can solve the tasks. Open your textbook to page 205, № 1029. in this task it is necessary to calculate the value of expressions:
Tasks appear on the computer. As they are solved, a picture appears with the image of a boat, which, when fully assembled, sails away.
No. 1031 Calculate:

Solving this task on a computer, the rocket gradually develops, solving the last example, the rocket flies away. The teacher gives a little information to the students: “Every year, spaceships take off to the stars from the Kazakhstani land from the Baikonur Cosmodrome. Near Baikonur, Kazakhstan is building its new Baiterek cosmodrome.
No. 1035. Task.
How far will a car travel in 4 hours if the speed of the car is 74.8 km/h.

This task is accompanied by sound design and displaying a brief condition of the task on the monitor. If the problem is solved, right, then the car starts to move forward to the finish flag.
№ 1033. Write decimals as percentages.
0,2 = 20%; 0,5 = 50%; 0,75 = 75%; 0,92 = 92%; 1,24 =1 24%; 3,5 = 350%; 5,61= 561%.
Solving each example, when the answer appears, a letter appears, resulting in the word Well done.

The teacher asks Komposha, why would this word appear? Komposha replies: “Well done, guys!” and say goodbye to everyone.
The teacher sums up the lesson and assigns grades.
In this tutorial, we'll look at each of these operations one by one.
Lesson contentAdding decimals
As we know, a decimal fraction consists of an integer part and a fractional part. When adding decimals, the integer and fractional parts are added separately.
For example, let's add the decimals 3.2 and 5.3. It is more convenient to add decimal fractions in a column.
First, we write these two fractions in a column, while the integer parts must be under the integer parts, and the fractional ones under the fractional ones. In school, this requirement is called "comma under comma" .
Let's write the fractions in a column so that the comma is under the comma:
We add the fractional parts: 2 + 3 = 5. We write down the five in the fractional part of our answer:
Now we add up the integer parts: 3 + 5 = 8. We write the eight in the integer part of our answer:
Now we separate the integer part from the fractional part with a comma. To do this, we again follow the rule "comma under comma" :
Got the answer 8.5. So the expression 3.2 + 5.3 is equal to 8.5
3,2 + 5,3 = 8,5
In fact, not everything is as simple as it seems at first glance. Here, too, there are pitfalls, which we will now talk about.
Places in decimals
Decimals, like ordinary numbers, have their own digits. These are tenth places, hundredth places, thousandth places. In this case, the digits begin after the decimal point.
The first digit after the decimal point is responsible for the tenths place, the second digit after the decimal point for the hundredths place, the third digit after the decimal point for the thousandths place.
Decimal digits store some useful information. In particular, they report how many tenths, hundredths, and thousandths are in a decimal.
For example, consider the decimal 0.345
The position where the triple is located is called tenth place
The position where the four is located is called hundredths place
The position where the five is located is called thousandths

Let's look at this figure. We see that in the category of tenths there is a three. This suggests that there are three tenths in the decimal fraction 0.345.
If we add the fractions, and then we get the original decimal fraction 0.345

We first got the answer, but converted it to decimal and got 0.345.
Adding decimals follows the same rules as adding ordinary numbers. The addition of decimal fractions occurs by digits: tenths are added to tenths, hundredths to hundredths, thousandths to thousandths.
Therefore, when adding decimal fractions, it is required to follow the rule "comma under comma". A comma under a comma provides the same order in which tenths are added to tenths, hundredths to hundredths, thousandths to thousandths.
Example 1 Find the value of the expression 1.5 + 3.4
First of all, we add the fractional parts 5 + 4 = 9. We write the nine in the fractional part of our answer:
Now we add up the integer parts 1 + 3 = 4. We write down the four in the integer part of our answer:
Now we separate the integer part from the fractional part with a comma. To do this, we again observe the rule "comma under a comma":
Got the answer 4.9. So the value of the expression 1.5 + 3.4 is 4.9
Example 2 Find the value of the expression: 3.51 + 1.22
We write this expression in a column, observing the rule "comma under a comma"
First of all, add the fractional part, namely the hundredths 1+2=3. We write the triple in the hundredth part of our answer:
Now add tenths of 5+2=7. We write down the seven in the tenth part of our answer:
Now add the whole parts 3+1=4. We write down the four in the whole part of our answer:
We separate the integer part from the fractional part with a comma, observing the “comma under the comma” rule:
Got the answer 4.73. So the value of the expression 3.51 + 1.22 is 4.73
3,51 + 1,22 = 4,73
As with ordinary numbers, when adding decimal fractions, . In this case, one digit is written in the answer, and the rest are transferred to the next digit.
Example 3 Find the value of the expression 2.65 + 3.27
We write this expression in a column:
Add hundredths of 5+7=12. The number 12 will not fit in the hundredth part of our answer. Therefore, in the hundredth part, we write the number 2, and transfer the unit to the next bit:
Now we add the tenths of 6+2=8 plus the unit that we got from the previous operation, we get 9. We write the number 9 in the tenth of our answer:
Now add the whole parts 2+3=5. We write the number 5 in the integer part of our answer:
Got the answer 5.92. So the value of the expression 2.65 + 3.27 is 5.92
2,65 + 3,27 = 5,92
Example 4 Find the value of the expression 9.5 + 2.8
Write this expression in a column
We add the fractional parts 5 + 8 = 13. The number 13 will not fit in the fractional part of our answer, so we first write down the number 3, and transfer the unit to the next digit, or rather transfer it to the integer part:
Now we add the integer parts 9+2=11 plus the unit that we got from the previous operation, we get 12. We write the number 12 in the integer part of our answer:
Separate the integer part from the fractional part with a comma:
Got the answer 12.3. So the value of the expression 9.5 + 2.8 is 12.3
9,5 + 2,8 = 12,3
When adding decimal fractions, the number of digits after the decimal point in both fractions must be the same. If there are not enough digits, then these places in the fractional part are filled with zeros.
Example 5. Find the value of the expression: 12.725 + 1.7
Before writing this expression in a column, let's make the number of digits after the decimal point in both fractions the same. The decimal fraction 12.725 has three digits after the decimal point, while the fraction 1.7 has only one. So in the fraction 1.7 at the end you need to add two zeros. Then we get the fraction 1,700. Now you can write this expression in a column and start calculating:

Add thousandths of 5+0=5. We write the number 5 in the thousandth part of our answer:

Add hundredths of 2+0=2. We write the number 2 in the hundredth part of our answer:

Add tenths of 7+7=14. The number 14 will not fit in a tenth of our answer. Therefore, we first write down the number 4, and transfer the unit to the next bit:

Now we add the integer parts 12+1=13 plus the unit that we got from the previous operation, we get 14. We write the number 14 in the integer part of our answer:

Separate the integer part from the fractional part with a comma:

Got the answer 14,425. So the value of the expression 12.725+1.700 is 14.425
12,725+ 1,700 = 14,425
Subtraction of decimals
When subtracting decimal fractions, you must follow the same rules as when adding: “a comma under a comma” and “an equal number of digits after a decimal point”.
Example 1 Find the value of the expression 2.5 − 2.2
We write this expression in a column, observing the “comma under comma” rule:
We calculate the fractional part 5−2=3. We write the number 3 in the tenth part of our answer:
Calculate the integer part 2−2=0. We write zero in the integer part of our answer:
Separate the integer part from the fractional part with a comma:
We got the answer 0.3. So the value of the expression 2.5 − 2.2 is equal to 0.3
2,5 − 2,2 = 0,3
Example 2 Find the value of the expression 7.353 - 3.1
This expression has a different number of digits after the decimal point. In the fraction 7.353 there are three digits after the decimal point, and in the fraction 3.1 there is only one. This means that in the fraction 3.1, two zeros must be added at the end to make the number of digits in both fractions the same. Then we get 3,100.
Now you can write this expression in a column and calculate it:

Got the answer 4,253. So the value of the expression 7.353 − 3.1 is 4.253
7,353 — 3,1 = 4,253
As with ordinary numbers, sometimes you will have to borrow one from the adjacent bit if subtraction becomes impossible.
Example 3 Find the value of the expression 3.46 − 2.39
Subtract hundredths of 6−9. From the number 6 do not subtract the number 9. Therefore, you need to take a unit from the adjacent digit. Having borrowed one from the neighboring digit, the number 6 turns into the number 16. Now we can calculate the hundredths of 16−9=7. We write down the seven in the hundredth part of our answer:
Now subtract tenths. Since we took one unit in the category of tenths, the figure that was located there decreased by one unit. In other words, the tenth place is now not the number 4, but the number 3. Let's calculate the tenths of 3−3=0. We write zero in the tenth part of our answer:
Now subtract the integer parts 3−2=1. We write the unit in the integer part of our answer:
Separate the integer part from the fractional part with a comma:
Got the answer 1.07. So the value of the expression 3.46−2.39 is equal to 1.07
3,46−2,39=1,07
Example 4. Find the value of the expression 3−1.2
This example subtracts a decimal from an integer. Let's write this expression in a column so that the integer part of the decimal fraction 1.23 is under the number 3
Now let's make the number of digits after the decimal point the same. To do this, after the number 3, put a comma and add one zero:
Now subtract tenths: 0−2. Do not subtract the number 2 from zero. Therefore, you need to take a unit from the adjacent digit. By borrowing one from the adjacent digit, 0 turns into the number 10. Now you can calculate the tenths of 10−2=8. We write down the eight in the tenth part of our answer:
Now subtract the whole parts. Previously, the number 3 was located in the integer, but we borrowed one unit from it. As a result, it turned into the number 2. Therefore, we subtract 1 from 2. 2−1=1. We write the unit in the integer part of our answer:
Separate the integer part from the fractional part with a comma:
Got the answer 1.8. So the value of the expression 3−1.2 is 1.8
Decimal multiplication
Multiplying decimals is easy and even fun. To multiply decimals, you need to multiply them like regular numbers, ignoring the commas.
Having received the answer, it is necessary to separate the integer part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in both fractions, then count the same number of digits on the right in the answer and put a comma.
Example 1 Find the value of the expression 2.5 × 1.5
We multiply these decimal fractions as ordinary numbers, ignoring the commas. To ignore the commas, you can temporarily imagine that they are absent altogether:

We got 375. In this number, it is necessary to separate the whole part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in fractions of 2.5 and 1.5. In the first fraction there is one digit after the decimal point, in the second fraction there is also one. A total of two numbers.
We return to the number 375 and begin to move from right to left. We need to count two digits from the right and put a comma:

Got the answer 3.75. So the value of the expression 2.5 × 1.5 is 3.75
2.5 x 1.5 = 3.75
Example 2 Find the value of the expression 12.85 × 2.7
Let's multiply these decimals, ignoring the commas:

We got 34695. In this number, you need to separate the integer part from the fractional part with a comma. To do this, you need to calculate the number of digits after the decimal point in fractions of 12.85 and 2.7. In the fraction 12.85 there are two digits after the decimal point, in the fraction 2.7 there is one digit - a total of three digits.
We return to the number 34695 and begin to move from right to left. We need to count three digits from the right and put a comma:

Got the answer 34,695. So the value of the expression 12.85 × 2.7 is 34.695
12.85 x 2.7 = 34.695
Multiplying a decimal by a regular number
Sometimes there are situations when you need to multiply a decimal fraction by a regular number.
To multiply a decimal and an ordinary number, you need to multiply them, regardless of the comma in the decimal. Having received the answer, it is necessary to separate the integer part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in the decimal fraction, then in the answer, count the same number of digits to the right and put a comma.
For example, multiply 2.54 by 2
We multiply the decimal fraction 2.54 by the usual number 2, ignoring the comma:

We got the number 508. In this number, you need to separate the integer part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in the fraction 2.54. The fraction 2.54 has two digits after the decimal point.
We return to the number 508 and begin to move from right to left. We need to count two digits from the right and put a comma:

Got the answer 5.08. So the value of the expression 2.54 × 2 is 5.08
2.54 x 2 = 5.08
Multiplying decimals by 10, 100, 1000
Multiplying decimals by 10, 100, or 1000 is done in the same way as multiplying decimals by regular numbers. It is necessary to perform the multiplication, ignoring the comma in the decimal fraction, then in the answer, separate the integer part from the fractional part, counting the same number of digits on the right as there were digits after the decimal point in the decimal fraction.
For example, multiply 2.88 by 10
Let's multiply the decimal fraction 2.88 by 10, ignoring the comma in the decimal fraction:

We got 2880. In this number, you need to separate the whole part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in the fraction 2.88. We see that in the fraction 2.88 there are two digits after the decimal point.
We return to the number 2880 and begin to move from right to left. We need to count two digits from the right and put a comma:

Got the answer 28.80. We discard the last zero - we get 28.8. So the value of the expression 2.88 × 10 is 28.8
2.88 x 10 = 28.8
There is a second way to multiply decimal fractions by 10, 100, 1000. This method is much simpler and more convenient. It consists in the fact that the comma in the decimal fraction moves to the right by as many digits as there are zeros in the multiplier.
For example, let's solve the previous example 2.88×10 in this way. Without giving any calculations, we immediately look at the factor 10. We are interested in how many zeros are in it. We see that it has one zero. Now in the fraction 2.88 we move the decimal point to the right by one digit, we get 28.8.
2.88 x 10 = 28.8
Let's try to multiply 2.88 by 100. We immediately look at the factor 100. We are interested in how many zeros are in it. We see that it has two zeros. Now in the fraction 2.88 we move the decimal point to the right by two digits, we get 288
2.88 x 100 = 288
Let's try to multiply 2.88 by 1000. We immediately look at the factor 1000. We are interested in how many zeros are in it. We see that it has three zeros. Now in the fraction 2.88 we move the decimal point to the right by three digits. The third digit is not there, so we add another zero. As a result, we get 2880.
2.88 x 1000 = 2880
Multiplying decimals by 0.1 0.01 and 0.001
Multiplying decimals by 0.1, 0.01, and 0.001 works in the same way as multiplying a decimal by a decimal. It is necessary to multiply fractions like ordinary numbers, and put a comma in the answer, counting as many digits on the right as there are digits after the decimal point in both fractions.
For example, multiply 3.25 by 0.1
We multiply these fractions like ordinary numbers, ignoring the commas:

We got 325. In this number, you need to separate the whole part from the fractional part with a comma. To do this, you need to calculate the number of digits after the decimal point in fractions of 3.25 and 0.1. In the fraction 3.25 there are two digits after the decimal point, in the fraction 0.1 there is one digit. A total of three numbers.
We return to the number 325 and begin to move from right to left. We need to count three digits on the right and put a comma. After counting three digits, we find that the numbers are over. In this case, you need to add one zero and put a comma:

We got the answer 0.325. So the value of the expression 3.25 × 0.1 is 0.325
3.25 x 0.1 = 0.325
There is a second way to multiply decimals by 0.1, 0.01 and 0.001. This method is much easier and more convenient. It consists in the fact that the comma in the decimal fraction moves to the left by as many digits as there are zeros in the multiplier.
For example, let's solve the previous example 3.25 × 0.1 in this way. Without giving any calculations, we immediately look at the factor 0.1. We are interested in how many zeros are in it. We see that it has one zero. Now in the fraction 3.25 we move the decimal point to the left by one digit. Moving the comma one digit to the left, we see that there are no more digits before the three. In this case, add one zero and put a comma. As a result, we get 0.325
3.25 x 0.1 = 0.325
Let's try multiplying 3.25 by 0.01. Immediately look at the multiplier of 0.01. We are interested in how many zeros are in it. We see that it has two zeros. Now in the fraction 3.25 we move the comma to the left by two digits, we get 0.0325
3.25 x 0.01 = 0.0325
Let's try multiplying 3.25 by 0.001. Immediately look at the multiplier of 0.001. We are interested in how many zeros are in it. We see that it has three zeros. Now in the fraction 3.25 we move the decimal point to the left by three digits, we get 0.00325
3.25 × 0.001 = 0.00325
Do not confuse multiplying decimals by 0.1, 0.001 and 0.001 with multiplying by 10, 100, 1000. A common mistake most people make.
When multiplying by 10, 100, 1000, the comma is moved to the right by as many digits as there are zeros in the multiplier.
And when multiplying by 0.1, 0.01 and 0.001, the comma is moved to the left by as many digits as there are zeros in the multiplier.
If at first it is difficult to remember, you can use the first method, in which the multiplication is performed as with ordinary numbers. In the answer, you will need to separate the integer part from the fractional part by counting as many digits on the right as there are digits after the decimal point in both fractions.
Dividing a smaller number by a larger one. Advanced level.
In one of the previous lessons, we said that when dividing a smaller number by a larger one, a fraction is obtained, in the numerator of which is the dividend, and in the denominator is the divisor.
For example, to divide one apple into two, you need to write 1 (one apple) in the numerator, and write 2 (two friends) in the denominator. The result is a fraction. So each friend will get an apple. In other words, half an apple. A fraction is the answer to a problem how to split one apple between two

It turns out that you can solve this problem further if you divide 1 by 2. After all, a fractional bar in any fraction means division, which means that this division is also allowed in a fraction. But how? We are used to the fact that the dividend is always greater than the divisor. And here, on the contrary, the dividend is less than the divisor.
Everything will become clear if we remember that a fraction means crushing, dividing, dividing. This means that the unit can be split into as many parts as you like, and not just into two parts.
When dividing a smaller number by a larger one, a decimal fraction is obtained, in which the integer part will be 0 (zero). The fractional part can be anything.
So, let's divide 1 by 2. Let's solve this example with a corner:
One cannot be divided into two just like that. If you ask a question "how many twos are in one" , then the answer will be 0. Therefore, in private we write 0 and put a comma:
Now, as usual, we multiply the quotient by the divisor to pull out the remainder:
The moment has come when the unit can be split into two parts. To do this, add another zero to the right of the received one:
We got 10. We divide 10 by 2, we get 5. We write down the five in the fractional part of our answer:
Now we take out the last remainder to complete the calculation. Multiply 5 by 2, we get 10
We got the answer 0.5. So the fraction is 0.5
Half an apple can also be written using the decimal fraction 0.5. If we add these two halves (0.5 and 0.5), we again get the original one whole apple: 

This point can also be understood if we imagine how 1 cm is divided into two parts. If you divide 1 centimeter into 2 parts, you get 0.5 cm

Example 2 Find the value of expression 4:5
How many fives are in four? Not at all. We write in private 0 and put a comma:
We multiply 0 by 5, we get 0. We write zero under the four. Immediately subtract this zero from the dividend:
Now let's start splitting (dividing) the four into 5 parts. To do this, to the right of 4, we add zero and divide 40 by 5, we get 8. We write the eight in private.

We complete the example by multiplying 8 by 5, and get 40:

We got the answer 0.8. So the value of the expression 4: 5 is 0.8
Example 3 Find the value of expression 5: 125
How many numbers 125 are in five? Not at all. We write 0 in private and put a comma:

We multiply 0 by 5, we get 0. We write 0 under the five. Immediately subtract from the five 0
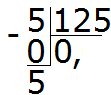
Now let's start splitting (dividing) the five into 125 parts. To do this, to the right of this five, we write zero:

Divide 50 by 125. How many numbers 125 are in 50? Not at all. So in the quotient we again write 0

We multiply 0 by 125, we get 0. We write this zero under 50. Immediately subtract 0 from 50
Now we divide the number 50 into 125 parts. To do this, to the right of 50, we write another zero:
Divide 500 by 125. How many numbers are 125 in the number 500. In the number 500 there are four numbers 125. We write the four in private:

We complete the example by multiplying 4 by 125, and get 500

We got the answer 0.04. So the value of the expression 5: 125 is 0.04
Division of numbers without a remainder
So, let's put a comma in the quotient after the unit, thereby indicating that the division of integer parts is over and we proceed to the fractional part:
Add zero to the remainder 4
Now we divide 40 by 5, we get 8. We write the eight in private:
40−40=0. Received 0 in the remainder. So the division is completely completed. Dividing 9 by 5 results in a decimal of 1.8:
9: 5 = 1,8
Example 2. Divide 84 by 5 without a remainder
First we divide 84 by 5 as usual with a remainder:

Received in private 16 and 4 more in the balance. Now we divide this remainder by 5. We put a comma in the private, and add 0 to the remainder 4

Now we divide 40 by 5, we get 8. We write the eight in the quotient after the decimal point:

and complete the example by checking if there is still a remainder:

Dividing a decimal by a regular number
A decimal fraction, as we know, consists of an integer and a fractional part. When dividing a decimal fraction by a regular number, first of all you need:
- divide the integer part of the decimal fraction by this number;
- after the integer part is divided, you need to immediately put a comma in the private part and continue the calculation, as in ordinary division.
For example, let's divide 4.8 by 2
Let's write this example as a corner:

Now let's divide the whole part by 2. Four divided by two is two. We write the deuce in private and immediately put a comma:

Now we multiply the quotient by the divisor and see if there is a remainder from the division:

4−4=0. The remainder is zero. We do not write zero yet, since the solution is not completed. Then we continue to calculate, as in ordinary division. Take down 8 and divide it by 2

8: 2 = 4. We write the four in the quotient and immediately multiply it by the divisor:

Got the answer 2.4. Expression value 4.8: 2 equals 2.4
Example 2 Find the value of the expression 8.43:3

We divide 8 by 3, we get 2. Immediately put a comma after the two:

Now we multiply the quotient by the divisor 2 × 3 = 6. We write the six under the eight and find the remainder:

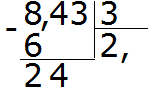
We divide 24 by 3, we get 8. We write the eight in private. We immediately multiply it by the divisor to find the remainder of the division:

24−24=0. The remainder is zero. Zero is not recorded yet. Take the last three of the dividend and divide by 3, we get 1. Immediately multiply 1 by 3 to complete this example:

Got the answer 2.81. So the value of the expression 8.43: 3 is equal to 2.81
Dividing a decimal by a decimal
To divide a decimal fraction into a decimal fraction, in the dividend and in the divisor, move the comma to the right by the same number of digits as there are after the decimal point in the divisor, and then divide by a regular number.
For example, divide 5.95 by 1.7
Let's write this expression as a corner

Now, in the dividend and in the divisor, we move the comma to the right by the same number of digits as there are after the decimal point in the divisor. The divisor has one digit after the decimal point. So we must move the comma to the right by one digit in the dividend and in the divisor. Transferring:

After moving the decimal point to the right by one digit, the decimal fraction 5.95 turned into a fraction 59.5. And the decimal fraction 1.7, after moving the decimal point to the right by one digit, turned into the usual number 17. And we already know how to divide the decimal fraction by the usual number. Further calculation is not difficult:

The comma is moved to the right to facilitate division. This is allowed due to the fact that when multiplying or dividing the dividend and the divisor by the same number, the quotient does not change. What does it mean?
This is one of the interesting features of division. It is called the private property. Consider expression 9: 3 = 3. If in this expression the dividend and the divisor are multiplied or divided by the same number, then the quotient 3 will not change.
Let's multiply the dividend and divisor by 2 and see what happens:
(9 × 2) : (3 × 2) = 18: 6 = 3
As can be seen from the example, the quotient has not changed.
The same thing happens when we carry a comma in the dividend and in the divisor. In the previous example, where we divided 5.91 by 1.7, we moved the comma one digit to the right in the dividend and divisor. After moving the comma, the fraction 5.91 was converted to the fraction 59.1 and the fraction 1.7 was converted to the usual number 17.
In fact, inside this process, multiplication by 10 took place. Here's what it looked like:
5.91 × 10 = 59.1
Therefore, the number of digits after the decimal point in the divisor depends on what the dividend and divisor will be multiplied by. In other words, the number of digits after the decimal point in the divisor will determine how many digits in the dividend and in the divisor the comma will be moved to the right.
Decimal division by 10, 100, 1000
Dividing a decimal by 10, 100, or 1000 is done in the same way as . For example, let's divide 2.1 by 10. Let's solve this example with a corner:

But there is also a second way. It's lighter. The essence of this method is that the comma in the dividend is moved to the left by as many digits as there are zeros in the divisor.
Let's solve the previous example in this way. 2.1: 10. We look at the divider. We are interested in how many zeros are in it. We see that there is one zero. So in the divisible 2.1, you need to move the comma to the left by one digit. We move the comma to the left by one digit and see that there are no more digits left. In this case, we add one more zero before the number. As a result, we get 0.21
Let's try to divide 2.1 by 100. There are two zeros in the number 100. So in the divisible 2.1, you need to move the comma to the left by two digits:
2,1: 100 = 0,021
Let's try to divide 2.1 by 1000. There are three zeros in the number 1000. So in the divisible 2.1, you need to move the comma to the left by three digits:
2,1: 1000 = 0,0021
Decimal division by 0.1, 0.01 and 0.001
Dividing a decimal by 0.1, 0.01, and 0.001 is done in the same way as . In the dividend and in the divisor, you need to move the comma to the right by as many digits as there are after the decimal point in the divisor.
For example, let's divide 6.3 by 0.1. First of all, we move the commas in the dividend and in the divisor to the right by the same number of digits as there are after the decimal point in the divisor. The divisor has one digit after the decimal point. So we move the commas in the dividend and in the divisor to the right by one digit.
After moving the decimal point to the right by one digit, the decimal fraction 6.3 turns into the usual number 63, and the decimal fraction 0.1, after moving the decimal point to the right by one digit, turns into one. And dividing 63 by 1 is very simple:
So the value of the expression 6.3: 0.1 is equal to 63
But there is also a second way. It's lighter. The essence of this method is that the comma in the dividend is transferred to the right by as many digits as there are zeros in the divisor.
Let's solve the previous example in this way. 6.3:0.1. Let's look at the divider. We are interested in how many zeros are in it. We see that there is one zero. So in the divisible 6.3, you need to move the comma to the right by one digit. We move the comma to the right by one digit and get 63
Let's try to divide 6.3 by 0.01. Divisor 0.01 has two zeros. So in the divisible 6.3, you need to move the comma to the right by two digits. But in the dividend there is only one digit after the decimal point. In this case, one more zero must be added at the end. As a result, we get 630
Let's try dividing 6.3 by 0.001. The divisor of 0.001 has three zeros. So in the divisible 6.3, you need to move the comma to the right by three digits:
6,3: 0,001 = 6300
Tasks for independent solution
Did you like the lesson?
Join our new Vkontakte group and start receiving notifications of new lessons
You already know that a * 10 = a + a + a + a + a + a + a + a + a + a. For example, 0.2 * 10 = 0.2 + 0.2 + 0.2 + 0.2 + 0.2 + 0.2 + 0.2 + 0.2 + 0.2 + 0.2 . It is easy to guess that this sum is equal to 2, i.e. 0.2 * 10 = 2.
Similarly, one can verify that:
5,2 * 10 = 52 ;
0,27 * 10 = 2,7 ;
1,253 * 10 = 12,53 ;
64,95 * 10 = 649,5 .
You probably guessed that when multiplying a decimal fraction by 10, you need to move the decimal point to the right by one digit in this fraction.
How do you multiply a decimal by 100?
We have: a * 100 = a * 10 * 10 . Then:
2,375 * 100 = 2,375 * 10 * 10 = 23,75 * 10 = 237,5 .
Arguing similarly, we get that:
3,2 * 100 = 320 ;
28,431 * 100 = 2843,1 ;
0,57964 * 100 = 57,964 .
Multiply the fraction 7.1212 by the number 1000.
We have: 7.1212 * 1000 = 7.1212 * 100 * 10 = 712.12 * 10 = 7121.2.
These examples illustrate the following rule.
To multiply a decimal fraction by 10, 100, 1,000, etc., you need to move the decimal point to the right in this fraction, respectively, by 1, 2, 3, etc. numbers.
So, if you move the comma to the right by 1, 2, 3, etc. numbers, then the fraction will increase by 10, 100, 1,000, etc., respectively. once.
Consequently, if you move the comma to the left by 1, 2, 3, etc. numbers, then the fraction will decrease by 10, 100, 1,000, etc., respectively. once .
Let us show that the decimal form of notation of fractions makes it possible to multiply them, guided by the rule of multiplication of natural numbers.
Let's find, for example, the product 3.4 * 1.23. Let's increase the first multiplier by 10 times, and the second by 100 times. This means that we have increased the product by 1,000 times.
Therefore, the product of natural numbers 34 and 123 is 1,000 times greater than the desired product.
We have: 34 * 123 = 4182. Then, to get an answer, the number 4,182 must be reduced by 1,000 times. Let's write: 4 182 \u003d 4 182.0. Moving the comma in 4182.0 three digits to the left, we get the number 4.182, which is 1000 times less than the number 4182. So 3.4 * 1.23 = 4.182 .
The same result can be obtained using the following rule.
To multiply two decimals:
1) multiply them as natural numbers, ignoring commas;
2) in the resulting product, separate with a comma on the right as many digits as there are after the commas in both factors together.
In cases where the product contains fewer digits than is required to be separated by a comma, the required number of zeros is added to the left before this product, and then the comma is moved to the left by the required number of digits.
For example, 2 * 3 = 6, then 0.2 * 3 = 0.006; 25 * 33 = 825, then 0.025 * 0.33 = 0.00825.
In cases where one of the factors is equal to 0.1; 0.01; 0.001, etc., it is convenient to use the following rule.
To multiply a decimal by 0.1 ; 0.01; 0.001, etc., it is necessary to move the comma to the left in this fraction, respectively, by 1, 2, 3, etc. numbers.
For example, 1.58 * 0.1 = 0.158; 324.7 * 0.01 = 3.247.
The properties of multiplication of natural numbers are also valid for fractional numbers:
ab = ba − commutative property of multiplication,
(ab) c = a(b c) − the associative property of multiplication,
a(b + c) = ab + ac is the distributive property of multiplication with respect to addition.
Like regular numbers.
2. We count the number of decimal places for the 1st decimal fraction and for the 2nd. We add up their number.
3. In the final result, we count from right to left such a number of digits as they turned out in the paragraph above, and put a comma.
Rules for multiplying decimals.
1. Multiply without paying attention to the comma.
2. In the product, we separate as many digits after the decimal point as there are after the commas in both factors together.
Multiplying a decimal fraction by a natural number, you must:
1. Multiply numbers, ignoring the comma;
2. As a result, we put a comma so that there are as many digits to the right of it as in a decimal fraction.
Multiplication of decimal fractions by a column.
Let's look at an example:
We write decimal fractions in a column and multiply them as natural numbers, ignoring the commas. Those. We consider 3.11 as 311, and 0.01 as 1.
The result is 311. Next, we count the number of decimal places (digits) for both fractions. There are 2 digits in the 1st decimal and 2 in the 2nd. The total number of digits after the decimal points:
2 + 2 = 4
We count from right to left four characters of the result. In the final result, there are fewer digits than you need to separate with a comma. In this case, it is necessary to add the missing number of zeros on the left.
In our case, the 1st digit is missing, so we add 1 zero on the left.

Note:
Multiplying any decimal fraction by 10, 100, 1000, and so on, the comma in the decimal fraction is moved to the right by as many places as there are zeros after the one.
For example:
70,1 . 10 = 701
0,023 . 100 = 2,3
5,6 . 1 000 = 5 600
Note:
To multiply a decimal by 0.1; 0.01; 0.001; and so on, you need to move the comma to the left in this fraction by as many characters as there are zeros in front of the unit.
We count zero integers!
For example:
12 . 0,1 = 1,2
0,05 . 0,1 = 0,005
1,256 . 0,01 = 0,012 56
In this article, we will consider such an action as multiplying decimal fractions. Let's start with the formulation of general principles, then we will show how to multiply one decimal fraction by another and consider the method of multiplication by a column. All definitions will be illustrated with examples. Then we will analyze how to correctly multiply decimal fractions by ordinary, as well as by mixed and natural numbers (including 100, 10, etc.)
As part of this material, we will only touch on the rules for multiplying positive fractions. Cases with negative numbers are discussed separately in the articles on the multiplication of rational and real numbers.
Let us formulate the general principles that must be followed when solving problems on the multiplication of decimal fractions.
To begin with, let us recall that decimal fractions are nothing more than a special form of writing ordinary fractions, therefore, the process of their multiplication can be reduced to the same for ordinary fractions. This rule works for both finite and infinite fractions: after converting them to ordinary fractions, it is easy to perform multiplication with them according to the rules we have already studied.
Let's see how such tasks are solved.
Example 1
Compute the product of 1.5 and 0.75.
Solution: First, replace the decimal fractions with ordinary ones. We know that 0.75 is 75/100 and 1.5 is 1510. We can reduce the fraction and extract the whole part. We will write the result 125 1000 as 1 , 125 .
Answer: 1 , 125 .
We can use the column counting method as we do for natural numbers.
Example 2
Multiply one periodic fraction 0 , (3) by another 2 , (36) .
First, let's reduce the original fractions to ordinary ones. We will be able to:
0 , (3) = 0 , 3 + 0 , 03 + 0 , 003 + 0 , 003 + . . . = 0 , 3 1 - 0 , 1 = 0 , 3 9 = 3 9 = 1 3 2 , (36) = 2 + 0 , 36 + 0 , 0036 + . . . = 2 + 0 , 36 1 - 0 , 01 = 2 + 36 99 = 2 + 4 11 = 2 4 11 = 26 11
Therefore, 0 , (3) 2 , (36) = 1 3 26 11 = 26 33 .
The resulting ordinary fraction can be reduced to decimal form by dividing the numerator by the denominator in a column:
Answer: 0 , (3) 2 , (36) = 0 , (78) .
If we have infinite non-periodic fractions in the condition of the problem, then we need to perform their preliminary rounding (see the article on rounding numbers if you forgot how to do this). After that, you can perform the multiplication operation with already rounded decimal fractions. Let's take an example.
Example 3
Compute the product of 5 , 382 ... and 0 , 2 .
Solution
We have an infinite fraction in the problem, which must first be rounded to hundredths. It turns out that 5, 382 ... ≈ 5, 38. Rounding the second factor to hundredths does not make sense. Now you can calculate the desired product and write down the answer: 5, 38 0, 2 = 538 100 2 10 = 1 076 1000 = 1, 076.
Answer: 5.382… 0.2 ≈ 1.076.
The column counting method can be applied not only to natural numbers. If we have decimals, we can multiply them in exactly the same way. Let's derive the rule:
Definition 1
Multiplication of decimal fractions by a column is performed in 2 steps:
1. We perform multiplication by a column, not paying attention to commas.
2. We put a decimal point in the final number, separating it as many digits on the right side as both factors contain decimal places together. If as a result there are not enough numbers for this, we add zeros on the left.
We will analyze examples of such calculations in practice.
Example 4
Multiply the decimals 63, 37 and 0, 12 by a column.
Solution
First of all, let's do the multiplication of numbers, ignoring the decimal points.

Now we need to put a comma in the right place. It will separate the four digits on the right side since the sum of the decimal places in both factors is 4 . You don't have to add zeros, because signs are enough.

Answer: 3.37 0.12 = 7.6044.
Example 5
Calculate how much is 3.2601 times 0.0254.
Solution
We count without commas. We get the following number:

We will put a comma separating 8 digits on the right side, because the original fractions together have 8 decimal places. But our result has only seven digits, and we can't do without extra zeros:

Answer: 3.2601 0.0254 = 0.08280654.
How to multiply a decimal by 0.001, 0.01, 01, etc
You often have to multiply decimals by such numbers, so it is important to be able to do this quickly and accurately. We write down a special rule that we will use in such multiplication:
Definition 2
If we multiply the decimal by 0, 1, 0, 01, etc., we end up with a number that looks like the original fraction, with the decimal point moved to the left by the required number of places. If there are not enough digits to transfer, you need to add zeros on the left.
So, to multiply 45, 34 by 0, 1, the comma must be moved in the original decimal fraction by one sign. We end up with 4,534.
Example 6
Multiply 9.4 by 0.0001.
Solution
We will have to move the comma to four digits according to the number of zeros in the second factor, but the numbers in the first are not enough for this. We assign the necessary zeros and get that 9, 4 0, 0001 = 0, 00094.
Answer: 0 , 00094 .
For infinite decimals, we use the same rule. So, for example, 0 , (18) 0 , 01 = 0 , 00 (18) or 94 , 938 … 0 , 1 = 9 , 4938 … . and etc.
The process of such a multiplication is no different from the action of multiplying two decimal fractions. It is convenient to use the multiplication method in a column if the condition of the problem contains a final decimal fraction. In this case, it is necessary to take into account all the rules that we talked about in the previous paragraph.
Example 7
Calculate how much will be 15 2, 27.
Solution
Multiply the original numbers by a column and separate the two commas.

Answer: 15 2.27 = 34.05.
If we perform the multiplication of a periodic decimal fraction by a natural number, we must first change the decimal fraction to an ordinary one.
Example 8
Compute the product of 0 , (42) and 22 .
We bring the periodic fraction to the form of an ordinary fraction.
0 , (42) = 0 , 42 + 0 , 0042 + 0 , 000042 + . . . = 0 , 42 1 - 0 , 01 = 0 , 42 0 , 99 = 42 99 = 14 33
0, 42 22 = 14 33 22 = 14 22 3 = 28 3 = 9 1 3
The final result can be written as a periodic decimal fraction as 9 , (3) .
Answer: 0 , (42) 22 = 9 , (3) .
Infinite fractions must be rounded before counting.
Example 9
Calculate how much will be 4 2 , 145 ... .
Solution
Let's round up to hundredths the original infinite decimal fraction. After that, we will come to the multiplication of a natural number and a final decimal fraction:
4 2, 145 ... ≈ 4 2, 15 = 8, 60.
Answer: 4 2.145 ... ≈ 8.60.
How to multiply a decimal by 1000, 100, 10, etc.
Multiplying a decimal fraction by 10, 100, etc. is often found in problems, so we will analyze this case separately. The basic multiplication rule is:
Definition 3
To multiply a decimal by 1000, 100, 10, etc., you need to move its comma by 3, 2, 1 digits depending on the multiplier and discard extra zeros on the left. If there are not enough digits to move the comma, we add as many zeros to the right as we need.
Let's show an example how to do it.
Example 10
Do the multiplication of 100 and 0.0783.
Solution
To do this, we need to move the decimal point by 2 digits to the right. We end up with 007 , 83 The zeros on the left can be discarded and the result can be written as 7 , 38 .
Answer: 0.0783 100 = 7.83.
Example 11
Multiply 0.02 by 10 thousand.
Solution: we will move the comma four digits to the right. In the original decimal fraction, we do not have enough signs for this, so we have to add zeros. In this case, three 0's will suffice. As a result, it turned out 0, 02000, move the comma and get 00200, 0. Ignoring the zeros on the left, we can write the answer as 200 .
Answer: 0.02 10,000 = 200.
The rule we have given will work in the same way in the case of infinite decimal fractions, but here you should be very careful about the period of the final fraction, since it is easy to make a mistake in it.
Example 12
Compute the product of 5.32 (672) times 1000 .
Solution: first of all, we will write the periodic fraction as 5, 32672672672 ..., so the probability of making a mistake will be less. After that, we can move the comma to the desired number of characters (three). As a result, we get 5326 , 726726 ... Let's enclose the period in brackets and write the answer as 5 326 , (726) .
Answer: 5 . 32 (672) 1 000 = 5 326 . (726) .
If in the conditions of the problem there are infinite non-periodic fractions that must be multiplied by ten, one hundred, one thousand, etc., do not forget to round them before multiplying.
To perform this type of multiplication, you need to represent the decimal fraction as an ordinary fraction and then follow the already familiar rules.
Example 13
Multiply 0 , 4 by 3 5 6
Solution
Let's first convert the decimal to a common fraction. We have: 0 , 4 = 4 10 = 2 5 .
We got the answer as a mixed number. You can write it as a periodic fraction 1, 5 (3) .
Answer: 1 , 5 (3) .
If an infinite non-periodic fraction is involved in the calculation, you need to round it up to a certain number and only then multiply it.
Example 14
Calculate the product of 3.5678. . . 2 3
Solution
We can represent the second factor as 2 3 = 0, 6666 …. Next, we round both factors to the thousandth place. After that, we will need to calculate the product of two final decimal fractions 3.568 and 0.667. Let's count the column and get the answer:

The final result must be rounded to thousandths, since it was to this category that we rounded the original numbers. We get that 2.379856 ≈ 2.380.
Answer: 3, 5678. . . 2 3 ≈ 2.380
If you notice a mistake in the text, please highlight it and press Ctrl+Enter




