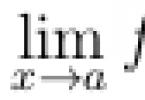From the path of integration.
Consider a curvilinear integral of the 2nd kind, where L– a curve connecting points M And N. Let the functions P(x, y) And Q(x, y) have continuous partial derivatives in some domain D, which contains the entire curve L. Let us determine the conditions under which the curvilinear integral under consideration does not depend on the shape of the curve L, but only on the location of the points M And N.
Let's draw two arbitrary curves MPN And MQN, lying in the area D and connecting points M And N(Fig. 1).
Q
M N Rice. 1.
Let's pretend that 
, that is 
Then where L– a closed contour made up of curves MPN And N.Q.M.(hence, it can be considered arbitrary). Thus, the condition for the independence of a curvilinear integral of the 2nd kind from the integration path is equivalent to the condition that such an integral over any closed contour is equal to zero.
Ticket No. 34.Surface integral of the first kind (over surface area). Applications (mass of a material surface, coordinates of the center of gravity, moments, area of a curved surface).
Consider an open surface S, limited by contour L, and divide it into parts by some curves S 1, S 2,…, S n. Let's select a point in each part M i and project this part onto a tangent plane to the surface passing through this point. We obtain in projection a flat figure with area T i. Let us call ρ the greatest distance between two points on any part of the surface S.
Definition 12.1. Let's call area S surfaces area sum limit T i at
Surface integral of the first kind.
Consider some surface S, limited by contour L, and break it into parts S 1, S 2,…, S p(we will also denote the area of each part S p). Let the value of the function be specified at each point of this surface f(x, y, z). Let's choose in each part S i point M i (x i , y i , z i) and compose the integral sum
. (12.2)
Definition 12.2. If there is a finite limit for the integral sum (12.2), independent of the method of dividing the surface into parts and the choice of points M i, then it is called surface integral of the first kind from the function f(M) = f(x, y, z) on the surface S and is designated
Comment. A surface integral of the 1st kind has the usual properties of integrals (linearity, summation of integrals of a given function over individual parts of the surface under consideration, etc.).
Geometric and physical meaning of a surface integral of the 1st kind.
If the integrand f(M)≡ 1, then from Definition 12.2 it follows that it is equal to the area of the surface under consideration S.
. (12.4)
Application of a surface integral of the 1st kind.
1. The area of a curved surface, the equation of which is z = f(x, y), can be found in the form:
(14.21)
(Ω – projection S to the O plane xy).
2. Surface mass
(14.22)
3. Moments:
Static moments of the surface relative to the coordinate planes O xy, O xz, O yz;
Moments of inertia of the surface relative to the coordinate axes;
Moments of inertia of the surface relative to coordinate planes;
- (14.26)
The moment of inertia of the surface relative to the origin.
4. Coordinates of the surface center of mass:
. (14.27)
Ticket number 35. Calculation of the surface integral of the 1st kind (reducing it to a multiple).
Let us restrict ourselves to the case when the surface S is given explicitly, that is, by an equation of the form z = φ(x, y). Moreover, from the definition of surface area it follows that
S i =, where Δ σi – projection area S i to the O plane xy, A γ i– angle between the O axis z and normal to the surface S at the point M i. It is known that
,
Where ( x i , y i , z i) – point coordinates M i. Therefore,
Substituting this expression into formula (12.2), we obtain that
,
Where the summation on the right is carried out over the region Ω of the O plane xy, which is the projection onto this surface plane S(Fig. 1).
S: z=φ(x,y)
ΔσiΩ
In this case, on the right side, an integral sum is obtained for a function of two variables over a flat region, which in the limit at gives a double integral. Thus, a formula has been obtained that allows us to reduce the calculation of a surface integral of the 1st kind to the calculation of a double integral:
Comment. Let us clarify once again that on the left side of formula (12.5) there is surface integral, and on the right - double.
Ticket number 36.Surface integral of the second kind. Vector field flow. Relationship between surface integrals of the first and second kind.
Vector field flow.
Consider the vector field A (M), defined in the spatial domain G, oriented smooth surface S G and the field of unit normals P (M) on the selected side of the surface S.
Definition 13.3. Surface integral of the 1st kind
,
(13.1)
Where An is the scalar product of the corresponding vectors, and A p– vector projection A to the normal direction is called vector field flow A(M) through the selected side of the surface S .
Remark 1. If you choose the other side of the surface, then the normal, and, consequently, the flux will change sign.
Remark 2. If the vector A specifies the speed of fluid flow at a given point, then integral (13.1) determines the amount of fluid flowing per unit time through the surface S in a positive direction (hence the common term "flow").
Let a flat vector field be given. In what follows we will assume that the functions P and Q are continuous, together with their derivatives, in some region O of the plane
Let us consider two arbitrary points in the region G. These points can be connected by different lines lying in the region along which the values of the curvilinear integral are generally different.
So, for example, consider the curvilinear integral
and two dots. Let's calculate this integral, firstly, along the straight line connecting points A and B, and, secondly, along the arc of the parabola connecting these same points. Applying the rules for calculating the curvilinear integral, we find
a) along the segment
b) along the arc of the parabola:
Thus, we see that the values of the curvilinear integral depend on the path of integration, that is, they depend on the type of line connecting points A and B. On the contrary, as is easy to check, the curvilinear integral along the same lines connecting the points gives the same thing value equal to .
The analyzed examples show that curvilinear integrals calculated along different paths connecting two given points are in some cases different from each other, and in other cases they take on the same value.
Let A and B be two arbitrary points of a region G. Consider various curves lying in the region G and connecting points A and B.
If the line integral along any of these paths takes the same value, then it is said to be independent of the path of integration.
The next two theorems give conditions under which the line integral is independent of the path of integration.
Theorem 1. In order for a curvilinear integral in some domain G to be independent of the path of integration, it is necessary and sufficient that the integral over any closed contour lying in this domain be equal to zero.
Proof. Adequacy.
Let the integral over any closed contour drawn in the region G be equal to zero. Let us show that this integral does not depend on the path of integration. In fact, let A and B be two points belonging to the region G. Let us connect these points by two different, arbitrarily chosen curves lying in the region G (Fig. 257).
Let us show that the arcs form a closed contour. Taking into account the properties of curvilinear integrals, we obtain
because . But according to the condition, it is like a closed loop integral.
Therefore, or Thus, the line integral does not depend on the path of integration.
Necessity. Let the curvilinear integral in the domain G be independent of the path of integration. Let us show that the integral over any closed contour lying in this region is equal to zero. In fact, let us consider an arbitrary closed contour lying in the region G, and take two arbitrary points A and B on it (see Fig. 257). Then
because according to the condition . So, the integral over any closed contour L lying in the region G is equal to zero.
The following theorem gives conditions convenient for practical use, under which the curvilinear integral does not depend on the path of integration.
Theorem 2.
In order for a curvilinear integral to be independent of the path of integration in a simply connected domain, it is necessary and sufficient that the condition be satisfied at each point in this domain
Proof. Adequacy. Let us show in the domain that the curvilinear integral over any closed contour L lying in the domain G is equal to zero. Let us consider an area a bounded by a contour L. Due to the simply connected nature of the region G, the area a entirely belongs to this area. Based on the Ostrogradsky-Green formula, in particular, on the site Therefore and therefore, . So, the integral over any closed contour L in the region G is equal to zero. Based on Theorem 1, we conclude that the curvilinear integral does not depend on the path of integration.
Necessity. Let the curvilinear integral be independent of the path of integration in some domain Q. Let us show that at all points of the domain
Let us assume the opposite, i.e., that at some point in the region Let, for definiteness, . Due to the assumption of continuity of partial derivatives, the difference will also be a continuous function. Consequently, around a point it is possible to describe a circle a (lying in the region G), at all points of which, as at the point, the difference will be positive. Let us apply the Ostrogradsky-Green formula to the circle.
A region is called simply connected if its boundary is a connected set. A region is called n-connected if its boundary splits into n-connected sets.
Comment. Green's formula is also true for multiply connected regions.
In order for the integral (A, B – any points from D) to not depend on the path of integration (but only on the initial and final points A, B), it is necessary and sufficient that along any closed curve (along any contour) lying in D the integral was equal to zero =0
Proof (necessity). Let (4) be independent of the integration path. Consider an arbitrary contour C lying in the region D and choose two arbitrary points A, B on this contour. Then curve C can be represented as the union of two curves AB=G2, AB=G1, C=Г - 1 + G2.
Theorem 1. In order for a curvilinear integral to be independent of the path of integration in D, it is necessary and sufficient that
in area D. Sufficiency. If this is true, then Green’s formula for any contour C will be 
whence the required statement follows by the lemma. Necessity. By lemma for any contour = 0. Then, by Green's formula for the area D bounded by this contour = 0. By the mean value theorem = mD or = = 0. Passing to the limit, contracting the contour to a point, we obtain that at this point.
Theorem 2. In order for the curvilinear integral (4) to be independent of the path of integration in D, it is necessary and sufficient that the integrand expression Pdx+Qdy be the total differential of some function u in the domain D. du = Pdx+Qdy. Adequacy. Let it be fulfilled, then Necessity. Let the integral be independent of the path of integration. We fix some point A0 in the domain D and define the function u(A) = u(x,y)=
In this case
XО (xО). Thus, there is a derivative =P. Similarly, it is checked that =Q. Under the assumptions made, the function u turns out to be continuously differentiable and du = Pdx+Qdy.
32-33. Definition of curvilinear integrals of the 1st and 2nd kind
Curvilinear integral over arc length (1st kind)
Let the function f(x,y) be defined and continuous at the points of the arc AB of a smooth curve K. Arbitrarily divide the arc into n elementary arcs by points t0..tn let lk be the length k of the particular arc. Let us take an arbitrary point N(k,k) on each elementary arc and multiply this point by the corresponding point. the length of the arc will be composed of three integral sums:
1
=
f(k,k)lk 2 = 
Р(k,k)хk 3 = 
Q(k,k)yk, where хk = x k -x k -1 , yk = y k -y k -1
The curvilinear integral of the 1st kind along the length of the arc will be called the limit of the integral sum 1, provided that max(lk) 0 
If the limit of the integral sum is 2 or 3 at 0, then this limit is called. curvilinear integral of the 2nd kind, a function P(x,y) or Q(x,y) along the curve l = AB and is denoted: 
or 
amount: 
+
It is customary to call it a general curvilinear integral of the 2nd kind and denote it by the symbol: 
in this case, the functions f(x,y), P(x,y), Q(x,y) are called integrable along the curve l = AB. The curve l itself is called a contour or by integration A is the initial point, B is the final integration point, dl is the differential of the arc length, therefore the curvilinear integral of the 1st kind is called. a curvilinear integral over an arc of a curve, and of the second kind – over a function..
From the definition of curvilinear integrals it follows that integrals of the 1st kind do not depend on the direction in which the curve l is run from A and B or from B and A. Curvilinear integral of the 1st kind along AB:
, for curvilinear integrals of the 2nd kind, a change in the direction of the curve leads to a change in sign:
In the case when l is a closed curve, i.e., point B coincides with point A, then of the two possible directions for traversing the closed contour, l is called positive the direction in which the area lying inside the contour remains to the left with respect to??? making a round, i.e. the direction of movement is counterclockwise. The opposite direction of traversal is called negative. The curvilinear integral AB along a closed contour l traversed in the positive direction will be denoted by the symbol:
For a spatial curve, one integral of the 1st kind is similarly introduced:
and three integrals of the 2nd kind:
the sum of the last three integrals is called. general curvilinear integral of the 2nd kind.
Some applications of curvilinear integrals of the 1st kind.
1.Integral 
- arc length AB
2.Mechanical meaning of the integral of the 1st kind.
If f(x,y) = (x,y) is the linear density of the material arc, then its mass: 
3.Coordinates of the center of mass of the material arc:
4. Moment of inertia of an arc lying in the oxy plane relative to the origin of coordinates and the axes of rotation ox, oy:
5. Geometric meaning of the integral of the 1st kind
Let the function z = f(x,y) – have the dimension of length f(x,y)>=0 at all points of the material arc lying in the oxy plane then:
, where S is the area of the cylindrical surface, the cat consists of perpendiculars to the okha plane, east. at points M(x,y) of the AB curve.
Some applications of curvilinear integrals of the 2nd kind.
Calculation of the area of a flat region D with boundary L
2. Work of force. Let a material point, under the influence of a force, move along a continuous flat curve BC, heading from B to C, the work of this force is:
2nd kind from the path of integration
Consider a curvilinear integral of the 2nd kind, where L is the curve connecting the points M and N. Let the functions P(x, y) and Q(x, y) have continuous partial derivatives in some domain D in which the curve L lies entirely. Let us determine the conditions under which the curvilinear integral under consideration does not depend on the shape of the curve L, but only on the location of the points M and N.
Let's draw two arbitrary curves MSN and MTN, lying in area D and connecting points M and N (Fig. 14).
Let us assume that, that is,
where L is a closed loop made up of the MSN and NTM curves (hence, it can be considered arbitrary). Thus, the condition for the independence of a curvilinear integral of the 2nd kind from the integration path is equivalent to the condition that such an integral over any closed contour is equal to zero.
Theorem 5 (Green's theorem). Let the functions P(x, y) and Q(x, y) and their partial derivatives and be continuous at all points of some domain D. Then, in order for any closed contour L lying in the domain D to satisfy the condition
it is necessary and sufficient that = at all points of the region D.
Proof.
1) Sufficiency: let the condition = be satisfied. Let us consider an arbitrary closed contour L in the region D, bounding the region S, and write Green’s formula for it:
So, sufficiency has been proven.
2) Necessity: suppose that the condition is satisfied at every point of the region D, but there is at least one point of this region at which -? 0. Let, for example, at the point P(x0, y0) we have: - > 0. Since the left side of the inequality contains a continuous function, will it be positive and greater than some? > 0 in some small region D` containing the point P. Consequently,
From here, using Green’s formula, we obtain that
where L` is the contour limiting the area D`. This result contradicts the condition. Consequently, = at all points of the region D, which is what needed to be proved.
Remark 1. Similarly, for three-dimensional space it can be proven that the necessary and sufficient conditions for the independence of the curvilinear integral
from the integration path are:
Remark 2. If conditions (52) are met, the expression Pdx + Qdy + Rdz is the total differential of some function u. This allows us to reduce the calculation of a curvilinear integral to determining the difference between the values at both the final and initial points of the integration contour, since
In this case, the function and can be found using the formula
where (x0, y0, z0) is a point from region D, and C is an arbitrary constant. Indeed, it is easy to verify that the partial derivatives of the function and, given by formula (53), are equal to P, Q and R.
Example 10.
Calculate line integral of the 2nd kind
along an arbitrary curve connecting points (1, 1, 1) and (2, 3, 4).
Let us make sure that conditions (52) are met:
Therefore, the function exists. Let us find it using formula (53), putting x0 = y0 = z0 = 0. Then
Thus, the function is determined up to an arbitrary constant term. Let's take C = 0, then u = xyz. Hence,
30. Green's formula. Conditions for the independence of a curvilinear integral from the path of integration.
Green's formula: If C is the closed boundary of the domain D and the functions P(x,y) and Q(x,y) together with their first-order partial derivatives are continuous in the closed domain D (including the boundary of C), then Green's formula is valid:, and the bypass around contour C is selected so that area D remains on the left.
From lectures: Let functions P(x,y) and Q(x,y) be given, which are continuous in the domain D along with first-order partial derivatives. Integral over the boundary (L), entirely contained in the region D and containing all points in the region D: . The positive direction of the contour is when the limited part of the contour is to the left.
Condition for the independence of a curvilinear integral of the 2nd kind from the integration path. A necessary and sufficient condition for the fact that the curvilinear integral of the first kind connecting the points M1 and M2 does not depend on the path of integration, but depends only on the starting and ending points, is the equality:.
.
31. Surface integrals of the first and second kind, their basic properties and calculation.
– specifying the surface.
Let us project S onto the xy plane and obtain a region D. We divide the region D with a grid of lines into parts called Di. From each point of each line we draw lines parallel to z, then S will be divided into Si. Let's make an integral sum: . Let us direct the maximum diameter Di to zero:, we obtain:
This is a surface integral of the first kind
This is how a surface integral of the first kind is calculated.
Definition in brief. If there is a finite limit of the integral sum, independent of the method of partitioning S into elementary sections Si and the choice of points, then it is called a surface integral of the first kind.
When moving from variables x and y to u and v:
P 
a surface integral has all the properties of an ordinary integral. See questions above.
Definition of a surface integral of the second kind, its basic properties and calculation. Connection with the integral of the first kind.
Let a surface S be given, bounded by a line L (Fig. 3.10). Let us take some contour L on the surface S that has no common points with the boundary L. At point M of the contour L we can restore two normals to the surface S. Let us choose one of these directions. We trace point M along the contour L with the selected normal direction.
If point M returns to its original position with the same direction of the normal (and not the opposite), then the surface S is called two-sided. We will only consider two-sided surfaces. A two-sided surface is any smooth surface with the equation .
Let S be a two-sided open surface bounded by a line L that has no self-intersection points. Let's choose a certain side of the surface. We will call the positive direction of traversing the contour L such a direction in which, when moving along the selected side of the surface, the surface itself remains to the left. A two-sided surface with a positive direction for traversing the contours established on it in this way is called an oriented surface.
Let's move on to constructing a surface integral of the second kind. Let us take a two-sided surface S in space, consisting of a finite number of pieces, each of which is given by an equation of the form or is a cylindrical surface with generators parallel to the Oz axis.
Let R(x,y,z) be a function defined and continuous on the surface S. Using a network of lines, we divide S arbitrarily into n “elementary” sections ΔS1, ΔS2, ..., ΔSi, ..., ΔSn, which have no common internal points. On each section ΔSi we arbitrarily select a point Mi(xi,yi,zi) (i=1,...,n). Let (ΔSi)xy be the area of the projection of the section ΔSi onto the coordinate plane Oxy, taken with the “+” sign, if the normal to the surface S at the point Mi(xi,yi,zi) (i=1,...,n) forms with the Oz axis is an acute angle, and with a “–” sign if this angle is obtuse. Let's compose the integral sum for the function R(x,y,z) over the surface S in the variables x,y: . Let λ be the largest of the diameters ΔSi (i = 1, ..., n).
If there is a finite limit that does not depend on the method of partitioning the surface S into “elementary” sections ΔSi and on the choice of points, then it is called the surface integral over the selected side of the surface S of the function R(x,y,z) along the coordinates x, y (or surface integral of the second kind) and is denoted 
.
Similarly, you can construct surface integrals over coordinates x, z or y, z along the corresponding side of the surface, i.e. 
And 
.
If all these integrals exist, then we can introduce a “general” integral over the selected side of the surface: .
A surface integral of the second kind has the usual properties of an integral. We only note that any surface integral of the second kind changes sign when the side of the surface changes.
Relationship between surface integrals of the first and second kind.
Let the surface S be given by the equation: z = f(x,y), and f(x,y), f"x(x,y), f"y(x,y) are continuous functions in the closed domain τ (projections of the surface S to the coordinate plane Oxy), and the function R(x,y,z) is continuous on the surface S. The normal to the surface S, having direction cosines cos α, cos β, cos γ, is chosen to the upper side of the surface S. Then .
For the general case we have:
= 
| " |
