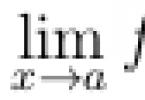Formulas and laws of logic
During the introductory lesson on basics of mathematical logic, we became acquainted with the basic concepts of this branch of mathematics, and now the topic is receiving a natural continuation. In addition to new theoretical, or rather not even theoretical - but general educational material, practical tasks await us, and therefore if you came to this page from a search engine and/or are poorly versed in the material, then please follow the above link and start from the previous article. In addition, for practice we will need 5 truth tables logical operations which I highly recommend rewrite by hand.
DO NOT remember, DO NOT print it out, but rather comprehend it again and rewrite it on paper with your own hand - so that they are before your eyes:
– table NOT;
– table I;
– OR table;
– implication table;
– table of equivalence.
It is very important. In principle, it would be convenient to number them “Table 1”, “Table 2”, etc., but I have repeatedly emphasized the flaw of this approach - as they say, in one source the table will be first, and in another - one hundred and first. Therefore, we will use “natural” names. Let's continue:
In fact, you are already familiar with the concept of a logical formula. I’ll give you a standard, but quite witty definition: formulas propositional algebras are called:
1) any elementary (simple) statements;
2) if and are formulas, then formulas are also expressions of the form
.
There are no other formulas.
In particular, a formula is any logical operation, such as logical multiplication. Pay attention to the second point - it allows recursive way to “create” an arbitrarily long formula. Because the ![]() - formulas, then - also a formula; since and are formulas, then
- formulas, then - also a formula; since and are formulas, then ![]() – also a formula, etc. Any elementary statement (again according to definition) can be included in the formula more than once.
– also a formula, etc. Any elementary statement (again according to definition) can be included in the formula more than once.
Formula Not is, for example, a notation - and here there is an obvious analogy with “algebraic garbage”, from which it is not clear whether numbers need to be added or multiplied.
The logical formula can be thought of as logical function. Let us write the same conjunction in functional form: ![]()
Elementary statements in this case also play the role of arguments (independent variables), which in classical logic can take on 2 meanings: true or lie. Below, for convenience, I will sometimes call simple statements variables.
A table describing a logical formula (function) is called, as has already been stated, truth table. Please – a familiar picture: 
The principle of forming a truth table is as follows: “at the input” you need to list all possible combinations truths and lies, which can take elementary statements (arguments). In this case, the formula includes two statements, and it is easy to find out that there are four such combinations. “At the output” we get the corresponding logical values of the entire formula (function).
It must be said that the “exit” here turned out to be “in one step,” but in the general case the logical formula is more complex. And in such “difficult cases” you need to comply order of execution of logical operations:
– negation is performed first;
– secondly – conjunction;
– then – disjunction;
– then implication;
– and finally, equivalence has the lowest priority.
So, for example, the entry implies that you first need to perform logical multiplication, and then logical addition: . Just like in “ordinary” algebra – “first we multiply, and then we add.”
The order of actions can be changed in the usual way - with brackets:
– here, first of all, the disjunction is performed and only then a “stronger” operation.
Probably everyone understands, but just in case, fireman: and this two different formulas! (both formally and substantively)
Let's create a truth table for the formula. This formula includes two elementary statements and “at the input” we need to list all possible combinations of ones and zeros. To avoid confusion and discrepancies, we will agree to list the combinations strictly in that order (which I actually de facto use from the very beginning):
The formula includes two logical operations, and according to their priority, first of all you need to perform negation statements. Well, let’s deny the “pe” column – we turn ones into zeros, and zeros into ones: 
In the second step, we look at the columns and apply to them OR operation. Looking ahead a little, I will say that the disjunction is commutative (and are the same thing), and therefore the columns can be analyzed in the usual order - from left to right. When performing logical addition, it is convenient to use the following applied reasoning: “If there are two zeros, we put a zero, if there is at least one one, we put one.”:
The truth table has been constructed. Now let’s remember the good old implication: 
...carefully, carefully... looking at the total columns.... In propositional algebra such formulas are called equivalent or identical:
(three horizontal lines are an identity icon)
In the 1st part of the lesson, I promised to express the implication through basic logical operations, and the fulfillment of the promise was not long in coming! Those who wish can put meaningful meaning into the implication (for example, “If it’s raining, it’s damp outside”) and independently analyze the equivalent statement.
Let's formulate general definition: the two formulas are called equivalent (identical), if they take the same values for any set of values included in these variable formulas (elementary statements). It is also said that “formulas are equivalent if their truth tables coincide”, but I don't really like this phrase.
Exercise 1
Create a truth table for the formula and make sure that the identity you are familiar with is correct.
Let us repeat the order of solving the problem once again:
1) Since the formula includes two variables, there will be a total of 4 possible sets of zeros and ones. We write them down in the order specified above.
2) Implications are “weaker” than conjunctions, but they are placed in parentheses. We fill out the column, and it is convenient to use the following applied reasoning: “if a zero follows from one, then we put zero, in all other cases - one”. Next, we fill in the column for implication, and at the same time, attention!– columns should be analyzed “from right to left”!
3) And at the final stage, fill in the final column. And here it is convenient to think like this: “if there are two units in the columns, then we put one, in all other cases – zero”.
And finally, we check the truth table equivalence .
Basic equivalences of propositional algebra
We have just met two of them, but the matter, of course, is not limited to them. There are quite a few identities and I will list the most important and most famous of them:
Commutativity of conjunction and commutativity of disjunction
Commutativity- this is commutability:
Rules familiar from 1st grade: “The product (sum) does not change by rearranging the factors (addends)”. But despite the apparent elementary nature of this property, it is not always true; in particular, it is non-commutative matrix multiplication (in general, they cannot be rearranged), A vector product of vectors– anticommutative (rearrangement of vectors entails a change of sign).
And, besides, here I again want to emphasize the formalism of mathematical logic. So, for example, the phrases “The student passed the exam and drank” And “The student drank and passed the exam” different from a content point of view, but indistinguishable from the standpoint of formal truth. ...Each of us knows such students, and for ethical reasons we will not voice specific names =)
Associativity of logical multiplication and addition
Or, if “in school style” – a coordinating property:
Distributive properties
Please note that in the 2nd case it will be incorrect to talk about “opening the parentheses”; in a certain sense, this is a “fiction” - after all, they can be removed altogether: , because multiplication is a stronger operation.
And again, these seemingly “banal” properties are not fulfilled in all algebraic systems, and, moreover, require proof (which we will talk about very soon). By the way, the second distributive law is not valid even in our “ordinary” algebra. And in fact:
Law of Idempotency
What to do, Latin...
Just some principle of a healthy psyche: “I and I are me”, “I or I are also me” =)
And here are several similar identities: ![]()
...hmm, I’m kind of stuck... so I might wake up with a PhD tomorrow =)
Law of double negation
Well, here an example with the Russian language suggests itself - everyone knows perfectly well that two particles “not” mean “yes”. And in order to enhance the emotional connotation of denial, three “nots” are often used:
– even with a tiny piece of evidence it worked!
Laws of absorption
- “Was there a boy?” =)
In the right identity, the parentheses can be omitted.
De Morgan's laws
Let's assume that the strict teacher (whose name you also know :)) gives an exam if - The student answered the 1st question And – The student answered the 2nd question. Then a statement saying that Student Not passed the exam, will be equivalent to the statement – Student Not answered the 1st question or to the 2nd question.
As noted above, equivalences are subject to proof, which is usually carried out using truth tables. In fact, we have already proved the equivalences expressing implication and equivalence, and now it is time to consolidate the technique for solving this problem.
Let's prove the identity. Since it includes a single statement, there are only two possible options at the input: one or zero. Next, we assign a single column and apply to them rule I:
As a result, the output is a formula, the truth of which coincides with the truth of the statement. Equivalence has been proven.
Yes, this proof is primitive (and some will say “stupid”), but a typical mathematics teacher will shake his soul for him. Therefore, even such simple things should not be treated with disdain.
Now let us verify, for example, the validity of de Morgan's law.
First, let's create a truth table for the left side. Since the disjunction is in parentheses, we perform it first, after which we negate the column: 
Next, let's create a truth table for the right side. Here, too, everything is transparent - first of all, we carry out “stronger” negations, then apply them to the columns rule I:
The results coincided, thus the identity was proven.
Any equivalence can be represented in the form identical to the true formula. It means that FOR ANY initial set of zeros and ones The “output” is strictly one. And there is a very simple explanation for this: since the truth tables coincide, then, of course, they are equivalent. Let us, for example, connect the left and right sides of the just proven de Morgan identity by equivalence: 
Or, more compactly:
Task 2
Prove the following equivalences:
b) ![]()
A short solution at the end of the lesson. Let's not be lazy! Try not only to create truth tables, but also clearly formulate conclusions. As I recently noted, neglecting simple things can be very, very expensive!
We continue to get acquainted with the laws of logic!
Yes, that’s absolutely right – we are already working hard with them:
True at , called identical to the true formula or law of logic.
Due to the previously justified transition from equivalence to an identically true formula, all of the identities listed above represent laws of logic.
Formula that takes value Lie at any set of values of the variables included in it, called identically false formula or contradiction.
A signature example of a contradiction from the ancient Greeks:
- no statement can be true and false at the same time.
The proof is trivial: 
The “output” contains only zeros, therefore the formula is really identical false.
However, any contradiction is also a law of logic, in particular: ![]()
It is impossible to cover such a vast topic in one single article, and therefore I will limit myself to just a few more laws:
Law of the excluded middle
– in classical logic, any statement is true or false and there is no third option. “To be or not to be” – that is the question.
Make a truth sign yourself and make sure that it is identically true formula.
Law of contraposition
This law was actively discussed when we discussed the essence necessary condition, we remember: “If it’s damp outside when it’s raining, then it follows that if it’s dry outside, then it definitely hasn’t rained.”.
It also follows from this law that if fair is straight theorem, then the statement, which is sometimes called opposite theorem.
If true reverse theorem, then by virtue of the law of contraposition, the theorem is also valid, the opposite of the reverse:
And again let's return to our meaningful examples: for statements – the number is divisible by 4, – the number is divisible by 2 fair straight And opposite theorems, but false reverse And the opposite of the reverse theorems. For the “adult” formulation of the Pythagorean theorem, all 4 “directions” are true.
Law of syllogism
Also a classic of the genre: “All oaks are trees, all trees are plants, therefore all oaks are plants.”.
Well, here again I would like to note the formalism of mathematical logic: if our strict Teacher thinks that a certain Student is an oak tree, then from a formal point of view this Student is certainly a plant =) ... although, if you think about it, then maybe from an informal point of view too = )
Let's create a truth table for the formula. In accordance with the priority of logical operations, we adhere to the following algorithm:
1) we carry out the implications and . Generally speaking, you can immediately perform the 3rd implication, but it is more convenient (and acceptable!) figure it out a little later;
2) apply to columns rule I;
3) now we execute;
4) and at the final step we apply the implication to the columns ![]() And .
And .
Feel free to control the process with your index and middle fingers :)) 
From the last column, I think everything is clear without comment:
, which was what needed to be proven.
Task 3
Find out whether the following formula is a law of logic:
A short solution at the end of the lesson. Oh, and I almost forgot - let's agree to list the original sets of zeros and ones in exactly the same order as when proving the law of syllogism. Of course, the lines can be rearranged, but this will make it very difficult to compare with my solution.
Converting logical formulas
In addition to their “logical” purpose, equivalences are widely used to transform and simplify formulas. Roughly speaking, one part of the identity can be exchanged for another. So, for example, if in a logical formula you come across a fragment, then according to the law of idempotency, instead of it you can (and should) write simply . If you see, then according to the law of absorption, simplify the notation to. And so on.
In addition, there is one more important thing: the identities are valid not only for elementary statements, but also for arbitrary formulas. For example:
![]()
![]()
, where – any (as complex as you like) formulas.
Let us transform, for example, the complex implication ![]() (1st identity):
(1st identity):
Next, we apply the “complex” de Morgan’s law to the bracket, and, due to the priority of operations, it is the law where ![]() :
:
The parentheses can be removed, because inside there is a “stronger” conjunction:
Well, with commutativity in general everything is simple - you don’t even need to designate anything... something about the law of syllogism has sunk into my soul :))
Thus, the law can be rewritten in a more intricate form:
Say out loud the logical chain “with an oak, a tree, a plant,” and you will understand that the substantive meaning of the law has not changed at all by rearranging the implications. Except that the wording has become more original.
As a workout, let's simplify the formula.
Where to begin? First of all, understand the order of actions: here the negation is applied to an entire parenthesis, which is “fastened” to the statement by a “slightly weaker” conjunction. Essentially, we have before us the logical product of two factors: . Of the two remaining operations, implication has the lowest priority, and therefore the entire formula has the following structure: .
Typically, the first step(s) is to get rid of equivalence and implication (if they are) and reduce the formula to three basic logical operations. What can I say... Logical.
(1) We use the identity ![]() . And in our case.
. And in our case.
This is usually followed by “showdowns” with brackets. First the whole solution, then the comments. To avoid “butter and butter”, I will use “regular” equality symbols: 
(2) We apply De Morgan’s law to the outer brackets, where .
1.3.1. STATEMENT
1.3.2. LOGICAL OPERATIONS
1.3.3. CONSTRUCTION OF TRUTH TABLES FOR LOGICAL EXPRESSIONS
1.3.4. PROPERTIES OF LOGICAL OPERATIONS
1.3.5. SOLVING LOGICAL PROBLEMS
1.3.6. LOGIC ELEMENTS
1. Read the presentation materials for the paragraph contained in the electronic appendix to the textbook. Does the presentation complement the information contained in the text of the paragraph?
2. Explain why the following sentences are not statements.
1) What color is this house?
2) The number X does not exceed one.
3) 4X+3.
4) Look out the window.
5) Drink tomato juice!
6) This topic is boring.
7) Ricky Martin is the most popular singer.
8) Have you been to the theater?

3. Give one example of true and false statements from biology, geography, computer science, history, mathematics, literature.

4. In the following statements, highlight the simple statements, indicating each of them with a letter; write down each compound statement using letters and logical operations signs.
1) The number 376 is even and three-digit.
2) In winter, children go ice skating or skiing.
3) We will celebrate the New Year at the dacha or on Red Square.
4) It is not true that the Sun moves around the Earth.
5) The Earth is shaped like a ball, which appears blue from space.
6) During a mathematics lesson, high school students answered the teacher’s questions and also wrote independent work.

5. Construct the negations of the following statements.


6. Let A = “Anya likes math lessons,” and B = “Anya likes chemistry lessons.” Express the following formulas in ordinary language:


7. A certain segment of the Internet consists of 1000 sites. The search server automatically compiled a table of keywords for sites in this segment. Here is its fragment:

920; 80.
8. Construct truth tables for the following logical expressions:


9. Provide proof of the logical laws discussed in the paragraph using truth tables.
10. Three numbers are given in the decimal number system: A=23, B=19, C=26. Convert A, B and C to the binary number system and perform bitwise logical operations (A v B) and C. Give the answer in the decimal number system.

11. Find the meanings of the expressions:


12. Find the value of the logical expression (x
1) 1
2) 2
3) 3
4) 4
1) 0. 2) 0. 3) 1. 4) 1.
13. Let A = “The first letter of the name is a vowel,” B = “The fourth letter of the name is a consonant.” Find the value of the logical expression A v B for the following names:
1) ELENA 2) VADIM 3) ANTON 4) FEDOR
1) 1. 2) 1. 3) 0. 4) 1.
14. The case of John, Brown and Smith is being examined. It is known that one of them found and hid the treasure. During the investigation, each of the suspects made two statements:
Smith: “I didn’t do it. Brown did it."
John: Brown is not guilty. Smith did it."
Brown: “I didn’t do it. John didn't do it."
The court found that one of them lied twice, the other told the truth twice, the third lied once and told the truth once. Which suspect should be acquitted?
Answer: Smith and John.
15. Alyosha, Borya and Grisha found an old vessel in the ground. Examining the amazing find, each made two assumptions:
1) Alyosha: “This is a Greek vessel and was made in the 5th century.”
2) Borya: “This is a Phoenician vessel and was made in the 3rd century.”
3) Grisha: “This vessel is not Greek and was made in the 4th century.”
The history teacher told the children that each of them was right in only one of two assumptions. Where and in what century was the vessel made?
Answer: Phoenician vessel, made in the 5th century.
16. Find out what signal should be at the output of the electronic circuit for each possible set of signals at the inputs. Make a table of how the circuit works. What logical expression describes the circuit?
The computer science lesson is designed for 10th grade students of a general education school, the curriculum of which includes the section “Algebra of Logic”. This topic is very difficult for students, so I, as a teacher, wanted to interest them in studying the laws of logic, simplifying logical expressions and approaching solving logical problems with interest. In the usual form, giving lessons on this topic is tedious and troublesome, and some of the definitions are not always clear to the children. In connection with the provision of information space, I had the opportunity to post my lessons in the “learning” shell. Students, having registered in it, can attend this course in their free time and re-read what was not clear in class. Some students, having missed lessons due to illness, make up for the missed topic at home or at school and are always ready for the next lesson. This form of teaching suited many children very much, and those laws that were incomprehensible to them are now learned in computer form much easier and faster. I offer one of these computer science lessons, which is conducted integratively with ICT.
Lesson Plan
- Explaining new material using a computer – 25 minutes.
- Basic concepts and definitions posted in “learning” - 10 minutes.
- Material for the curious – 5 minutes.
- Homework – 5 minutes.
1. Explanation of new material
Laws of formal logic
The simplest and most necessary true connections between thoughts are expressed in the basic laws of formal logic. These are the laws of identity, non-contradiction, excluded middle, sufficient reason.
These laws are fundamental because in logic they play a particularly important role and are the most general. They allow you to simplify logical expressions and build conclusions and proofs. The first three of the above laws were identified and formulated by Aristotle, and the law of sufficient reason - by G. Leibniz.
Law of identity: in the process of certain reasoning, every concept and judgment must be identical to itself.
Law of non-contradiction: it is impossible for one and the same eye to be and not to be inherent in the same thing in the same respect at the same time. That is, it is impossible to affirm and deny something at the same time.
Law of the excluded middle: of two contradictory propositions, one is true, the other is false, and the third is not given.
Law of Sufficient Reason: Every true thought must be sufficiently justified.
The last law says that proof of something presupposes the substantiation of precisely and only true thoughts. False thoughts cannot be proven. There is a good Latin proverb: “To make mistakes is common to every person, but to insist on a mistake is common only to a fool.” There is no formula for this law, since it is only substantive in nature. True judgments, factual material, statistical data, laws of science, axioms, proven theorems can be used as arguments to confirm a true thought.
Laws of propositional algebra
Propositional algebra (algebra of logic) is a section of mathematical logic that studies logical operations on statements and rules for transforming complex statements.
When solving many logical problems, it is often necessary to simplify the formulas obtained by formalizing their conditions. Simplification of formulas in propositional algebra is carried out on the basis of equivalent transformations based on basic logical laws.
The laws of propositional algebra (algebra of logic) are tautologies.
Sometimes these laws are called theorems.
In propositional algebra, logical laws are expressed in the form of equality of equivalent formulas. Among the laws, those that contain one variable stand out.
The first four laws below are the basic laws of propositional algebra.
Law of identity:
Every concept and judgment is identical to itself.
The law of identity means that in the process of reasoning one cannot replace one thought with another, one concept with another. If this law is violated, logical errors are possible.
For example, reasoning They rightly say that tongue will take you to Kyiv, but I bought smoked tongue yesterday, which means now I can safely go to Kyiv is incorrect, since the first and second words “language” mean different concepts.
In reasoning: Movement is eternal. Walking to school is movement. Therefore, going to school is forever the word “motion” is used in two different senses (the first - in the philosophical sense - as an attribute of matter, the second - in the everyday sense - as the action of moving in space), which leads to a false conclusion.
Law of non-contradiction:
A proposition and its negation cannot be true at the same time. That is, if the statement A- is true, then its negation not A must be false (and vice versa). Then their work will always be false.
It is this equality that is often used when simplifying complex logical expressions.
Sometimes this law is formulated as follows: two contradictory statements cannot be simultaneously true. Examples of non-compliance with the law of non-contradiction:
1. There is life on Mars and there is no life on Mars.
2. Olya graduated from high school and is in the Xth grade.
Law of the excluded middle:
At the same moment in time, a statement can be either true or false, there is no third option. True either A, or not A. Examples of implementation of the law of excluded middle:
1. The number 12345 is either even or odd, there is no third option.
2. The company operates at a loss or break-even.
3. This liquid may or may not be an acid.
The law of excluded middle is not a law recognized by all logicians as a universal law of logic. This law applies where cognition deals with a rigid situation: “either - or”, “true-false”. Where uncertainty occurs (for example, in reasoning about the future), the law of excluded middle often cannot be applied.
Consider the following statement: This sentence is false. It cannot be true because it states that it is false. But it cannot be false either, because then it would be true. This statement is neither true nor false, and therefore violates the law of excluded middle.
Paradox(Greek paradoxos - unexpected, strange) in this example arises due to the fact that the sentence refers to itself. Another well-known paradox is the hairdresser problem: In one city, a barber cuts the hair of all residents, except those who cut their own hair. Who cuts the barber's hair? In logic, due to its formality, it is not possible to obtain the form of such a self-referring statement. This once again confirms the idea that with the help of the algebra of logic it is impossible to express all possible thoughts and arguments. Let us show how, based on the definition of propositional equivalence, the remaining laws of propositional algebra can be obtained.
For example, let's determine what is equivalent (equivalent to) A(twice no A, i.e. negation of negation A). To do this, let's build a truth table:

By definition of equivalence, we must find the column whose values coincide with the values of the column A. This will be the column A.
Thus we can formulate law of doublenegatives:
If you negate a statement twice, the result is the original statement. For example, the statement A= Matroskin- cat is equivalent to the statement A = It is not true that Matroskin is not a cat.
In a similar way, the following laws can be derived and verified:
Properties of constants:

Laws of idempotency:
No matter how many times we repeat: the TV is on or the TV is on or the TV is on... the meaning of the statement will not change. Similar from repetition It's warm outside, it's warm outside... It won't get one degree warmer.
Laws of commutativity:
A v B = B v A
A & B = B & A
Operands A And IN In operations, disjunction and conjunction can be interchanged.
Laws of associativity:
A v(B v C) = (A v B) v C;
A & (B & C) = (A & B) & C.
If the expression uses only the disjunction operation or only the conjunction operation, then you can neglect the parentheses or arrange them arbitrarily.
Distributive laws:
A v (B & C) = (A v B) &(A v C)
(distributivity of disjunction
relative to conjunction)
A & (B v C) = (A & B) v (A & C)
(distributivity of the conjunction
regarding disjunction)
The distributive law of a conjunction relative to a disjunction is similar to the distributive law in algebra, but the distributive law of a disjunction relative to a conjunction has no analogue; it is valid only in logic. Therefore it is necessary to prove it. The proof is most conveniently carried out using a truth table:

Laws of absorption:
A v (A & B) = A
A & (A v B) = A
Prove the laws of absorption yourself.
De Morgan's laws:


Verbal formulations of De Morgan's laws:


Mnemonic rule: on the left side of the identity, the negation operation stands over the entire statement. On the right side, it seems to break and the negation stands over each of the simple statements, but at the same time the operation changes: disjunction to conjunction and vice versa.
Examples of implementation of De Morgan's law:
1) Statement It is not true that I know Arabic or Chinese identical to a statement I don't know Arabic and I don't know Chinese.
2) Statement It's not true that I learned the lesson and got a D in it. identical to a statement Either I didn't learn the lesson, or I didn't get a D in it.
Replacing the operations of implication and equivalence
The operations of implication and equivalence are sometimes not among the logical operations of a particular computer or translator from a programming language. However, to solve many problems these operations are necessary. There are rules for replacing these operations with sequences of negation, disjunction and conjunction operations.
So, replace the operation implications possible according to the following rule:
![]()
To replace the operation equivalence there are two rules:

It is easy to verify the validity of these formulas by constructing truth tables for the right and left sides of both identities.
Knowledge of the rules for replacing the operations of implication and equivalence helps, for example, to correctly construct the negation of implication.
Consider the following example.
Let the statement be given:
E = It is not true that if I win the competition, I will receive a prize.
Let A= I will win the competition
B = I will receive a prize.

Hence, E = I will win the competition, but I will not receive a prize.
The following rules are also of interest:
![]()
Their validity can also be proven using truth tables.
Their expression in natural language is interesting.
For example, the phrase
If Winnie the Pooh ate honey, then he is full
identical to the phrase
If Winnie the Pooh is not full, then he has not eaten honey.
Exercise: come up with example phrases based on these rules.
2. Basic concepts and definitions in Appendix 1
3. Material for the curious in Appendix 2
4. Homework
1) Learn the laws of logic using the course “Algebra of Logic”, located in the information space (www.learning.9151394.ru).
2) Check the proof of De Morgan's laws on a PC by constructing a truth table.
Applications
- Basic concepts and definitions (Appendix 1).
- Material for the curious (Appendix 2).
§ 1.3. Elements of algebra logic
Elements of algebra of logic. Questions and tasks
1. Read the presentation materials for the paragraph contained in the electronic appendix to the textbook. Does the presentation complement the information contained in the text of the paragraph?
2. Explain why the following sentences are not statements.
1) What color is this house?
2) The number X does not exceed one.
3) 4X + 3.
4) Look out the window.
5) Drink tomato juice!
6) This topic is boring.
7) Ricky Martin is the most popular singer.
8) Have you been to the theater?
3. Give one example of true and false statements from biology, geography, computer science, history, mathematics, literature.
4. In the following statements, highlight the simple statements, indicating each of them with a letter; write down each compound statement using letters and logical operations signs.
1) The number 376 is even and three-digit.
2) In winter, children go ice skating or skiing.
3) We will celebrate the New Year at the dacha or on Red Square.
4) It is not true that the Sun moves around the Earth.
5) The Earth is shaped like a ball, which appears blue from space.
6) During a mathematics lesson, high school students answered the teacher’s questions and also wrote independent work.
5. Construct the negations of the following statements.
1) Today the opera “Eugene Onegin” is being performed at the theater.
2) Every hunter wants to know where the pheasant is sitting.
3) The number 1 is a prime number.
4) Natural numbers ending in 0 are not prime numbers.
5) It is not true that the number 3 is not a divisor of the number 198.
6) Kolya solved all the tasks of the test.
7) At every school, some students are interested in sports.
8) Some mammals do not live on land.
6. Let A = “Anya likes math lessons”, and B = “Anya likes chemistry lessons”. Express the following formulas in ordinary language:

7. A certain segment of the Internet consists of 1000 sites. The search server automatically compiled a table of keywords for sites in this segment. Here is its fragment:

On request catfish & guppies 0 sites were found for your request catfish & swordtails- 20 sites, and upon request swordtails & guppies- 10 sites.
How many sites will be found by request? catfish | swordtails | guppy?
For how many sites in the segment under consideration is the statement false? “Catfish is the keyword of the site OR swordtails is the keyword of the site OR guppies is the keyword of the site”?
8. Construct truth tables for the following logical expressions:

9. Conduct a proof of the logical laws discussed in the paragraph using truth tables.