Instructions

Least positive period cosine is also equal to 2?. Consider the proof of this with an example functions y=cos(x). If T is arbitrary period om cosine, then cos(a+T)=cos(a). In the event that a=0, cos(T)=cos(0)=1. In view of this, the smallest positive value of T at which cos(x) = 1 is 2?.

Considering the fact that 2? – period sine and cosine, it will also be period ohm cotangent, as well as tangent, but not minimal, since, like , the smallest positive period tangent and cotangent are equal?. You can verify this by considering the following: the points corresponding to (x) and (x+?) on the trigonometric circle have diametrically opposite locations. The distance from point (x) to point (x+2?) corresponds to half a circle. By definition of tangent and cotangent tg(x+?)=tgx, and ctg(x+?)=ctgx, which means the smallest positive period cotangent and ?.

note

Do not confuse the functions y=cos(x) and y=sin(x) - having the same period, these functions are represented differently.

Helpful advice

For greater clarity, draw a trigonometric function for which the smallest positive period is calculated.

Sources:

• Handbook of mathematics, school mathematics, higher mathematics

Trigonometric functions periodic, that is, they are repeated after a certain period. Thanks to this, it is enough to study the function on this interval and extend the found properties to all other periods.

Instructions

To find the period of a trigonometric function raised to a power, evaluate the parity of the power. To reduce the standard period by half. For example, if you are given the function y=3 cos^2x, then the standard period 2P will decrease by 2 times, so the period will be equal to P. Please note that the functions tg, ctg are periodic to P to any degree.

From school mathematics lessons, everyone remembers a sine graph stretching into the distance in uniform waves. Many other functions have a similar property - repeating after a certain interval. They are called periodic. Periodicity is a very important property of a function, often encountered in various tasks. Therefore, it is useful to be able to determine whether a function is periodic.

Instructions

If F(x) is a function of the argument x, then it is called periodic if there is a number T such that for any x F(x + T) = F(x). This number T is called the period of the function.

There may be several periods. For example, the function F = const takes the same value for any value of the argument, and therefore any number can be considered its period.

Mathematicians are usually interested in the smallest non-zero period of a function. For brevity, it is simply called a period.

A classic example of periodic functions is trigonometric: sine, cosine and tangent. Their period is the same and equal to 2?, that is, sin(x) = sin(x + 2?) = sin(x + 4?) and so on. However, of course, trigonometric functions are not the only periodic ones.

For simple, basic functions, the only way to determine whether they are periodic or non-periodic is through calculation. But for complex functions there are already several simple rules.

If F(x) is a periodic function with period T, and a derivative is defined for it, then this derivative f(x) = F?(x) is also a periodic function with period T. After all, the value of the derivative at point x is equal to the tangent of the tangent angle graph its antiderivative at this point to the x-axis, and since the antiderivative is periodically repeated, the derivative must also be repeated. For example, the derivative of the function sin(x) is equal to cos(x), and it is periodic. Taking the derivative of cos(x) gives you –sin(x). The frequency remains unchanged.

However, the opposite is not always true. Thus, the function f(x) = const is periodic, but its antiderivative F(x) = const*x + C is not.

If F(x) is a periodic function with period T, then G(x) = a*F(kx + b), where a, b, and k are constants and k is not equal to zero - is also a periodic function, and its period is T/k. For example, sin(2x) is a periodic function, and its period is equal to?. This can be visually represented as follows: by multiplying x by some number, you seem to compress the graph of the function horizontally exactly that many times

If F1(x) and F2(x) are periodic functions, and their periods are equal to T1 and T2, respectively, then the sum of these functions can also be periodic. However, its period will not be a simple sum of periods T1 and T2. If the result of division T1/T2 is a rational number, then the sum of the functions is periodic, and its period is equal to the least common multiple (LCM) of the periods T1 and T2. For example, if the period of the first function is 12, and the period of the second is 15, then the period of their sum will be equal to LCM (12, 15) = 60.

This can be visually represented as follows: functions come with different “step widths,” but if the ratio of their widths is rational, then sooner or later (or rather, precisely through the LCM of steps), they will become equal again, and their sum will begin a new period.

However, if the ratio of periods is irrational, then the total function will not be periodic at all. For example, let F1(x) = x mod 2 (the remainder when x is divided by 2), and F2(x) = sin(x). T1 here will be equal to 2, and T2 will be equal to 2?. Is the period ratio equal? - an irrational number. Therefore, the function sin(x) + x mod 2 is not periodic.

Many mathematical functions have one feature that makes them easier to construct: periodicity, that is, the repeatability of the graph on a coordinate grid at regular intervals.

Instructions

The most famous periodic functions in mathematics are the sine and cosine functions. These functions have a wave-like character and a main period of 2P. Also a special case of a periodic function is f(x)=const. Any number is suitable for position x; this function does not have a main period, since it is a straight line.

In general, a function is periodic if there is an integer N that is non-zero and satisfies the rule f(x)=f(x+N), thus ensuring repeatability. The period of a function is the smallest number N, but not zero. That is, for example, the function sin x is equal to the function sin (x+2ПN), where N=±1, ±2, etc.

Sometimes a function may have a multiplier (for example, sin 2x), which will increase or decrease the period of the function. In order to find the period by graphics, it is necessary to determine the extrema of the function - the highest and lowest points of the function graph. Since sine and cosine waves have a wave-like nature, this is quite easy to do. From these points, construct perpendicular straight lines until they intersect with the X axis.

The distance from the upper extremum to the lower one will be half the period of the function. It is most convenient to calculate the period from the intersection of the graph with the Y axis and, accordingly, the zero mark on the x axis. After this, you need to multiply the resulting value by two and get the main period of the function.

To simplify the construction of sine and cosine graphs, it should be noted that if a function has an integer value, then its period will lengthen (that is, 2P must be multiplied by this coefficient) and the graph will look softer, smoother - and if the number is fractional, on the contrary, it will decrease and the graph will become more “sharp” and jumpy in appearance.

Goal: summarize and systematize students’ knowledge on the topic “Periodicity of Functions”; develop skills in applying the properties of a periodic function, finding the smallest positive period of a function, constructing graphs of periodic functions; promote interest in studying mathematics; cultivate observation and accuracy.

Equipment: computer, multimedia projector, task cards, slides, clocks, tables of ornaments, elements of folk crafts

“Mathematics is what people use to control nature and themselves.”
A.N. Kolmogorov

During the classes

I. Organizational stage.

Checking students' readiness for the lesson. Report the topic and objectives of the lesson.

II. Checking homework.

We check homework using samples and discuss the most difficult points.

III. Generalization and systematization of knowledge.

1. Oral frontal work.

Theory issues.

1) Form a definition of the period of the function
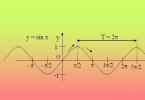
2) Name the smallest positive period of the functions y=sin(x), y=cos(x)
3). What is the smallest positive period of the functions y=tg(x), y=ctg(x)
4) Using a circle, prove the correctness of the relations:

y=sin(x) = sin(x+360º)
y=cos(x) = cos(x+360º)
y=tg(x) = tg(x+18 0º)
y=ctg(x) = ctg(x+180º)

tg(x+π n)=tgx, n € Z
ctg(x+π n)=ctgx, n € Z

sin(x+2π n)=sinx, n € Z
cos(x+2π n)=cosx, n € Z

5) How to plot a periodic function?

Oral exercises.

1) Prove the following relations

a) sin(740º) = sin(20º)
b) cos(54º) = cos(-1026º)
c) sin(-1000º) = sin(80º)

2. Prove that an angle of 540º is one of the periods of the function y= cos(2x)

3. Prove that an angle of 360º is one of the periods of the function y=tg(x)

4. Transform these expressions so that the angles included in them do not exceed 90º in absolute value.

a) tg375º
b) ctg530º
c) sin1268º
d) cos(-7363º)

5. Where did you come across the words PERIOD, PERIODICITY?

Student answers: A period in music is a structure in which a more or less complete musical thought is presented. A geological period is part of an era and is divided into epochs with a period from 35 to 90 million years.

Half-life of a radioactive substance. Periodic fraction. Periodicals are printed publications that appear within strictly defined deadlines. Mendeleev's periodic system.

6. The figures show parts of the graphs of periodic functions. Determine the period of the function. Determine the period of the function.

Answer: T=2; T=2; T=4; T=8.

7. Where in your life have you encountered the construction of repeating elements?

Student answer: Elements of ornaments, folk art.

IV. Collective problem solving.

(Solving problems on slides.)

Let's consider one of the ways to study a function for periodicity.

This method avoids the difficulties associated with proving that a particular period is the smallest, and also eliminates the need to touch upon questions about arithmetic operations on periodic functions and the periodicity of a complex function. The reasoning is based only on the definition of a periodic function and on the following fact: if T is the period of the function, then nT(n?0) is its period.

Problem 1. Find the smallest positive period of the function f(x)=1+3(x+q>5)

Solution: Assume that the T-period of this function. Then f(x+T)=f(x) for all x € D(f), i.e.

1+3(x+T+0.25)=1+3(x+0.25)
(x+T+0.25)=(x+0.25)

Let's put x=-0.25 and we get

(T)=0<=>T=n, n € Z

We have obtained that all periods of the function in question (if they exist) are among the integers. Let's choose the smallest positive number among these numbers. This 1 . Let's check whether it will actually be a period 1 .

f(x+1) =3(x+1+0.25)+1

Since (T+1)=(T) for any T, then f(x+1)=3((x+0.25)+1)+1=3(x+0.25)+1=f(x ), i.e. 1 – period f. Since 1 is the smallest of all positive integers, then T=1.

Problem 2. Show that the function f(x)=cos 2 (x) is periodic and find its main period.

Problem 3. Find the main period of the function

f(x)=sin(1.5x)+5cos(0.75x)

Let us assume the T-period of the function, then for any X the ratio is valid

sin1.5(x+T)+5cos0.75(x+T)=sin(1.5x)+5cos(0.75x)

If x=0, then

sin(1.5T)+5cos(0.75T)=sin0+5cos0

sin(1.5T)+5cos(0.75T)=5

If x=-T, then

sin0+5cos0=sin(-1.5T)+5cos0.75(-T)

5= – sin(1.5T)+5cos(0.75T)

sin(1.5T)+5cos(0.75T)=5 – sin(1.5T)+5cos(0.75T)=5

Adding it up, we get:

10cos(0.75T)=10

2π n, n € Z

Let us choose the smallest positive number from all the “suspicious” numbers for the period and check whether it is a period for f. This number

f(x+)=sin(1.5x+4π )+5cos(0.75x+2π )= sin(1.5x)+5cos(0.75x)=f(x)

This means that this is the main period of the function f.

Problem 4. Let’s check whether the function f(x)=sin(x) is periodic

Let T be the period of the function f. Then for any x

sin|x+Т|=sin|x|

If x=0, then sin|Т|=sin0, sin|Т|=0 Т=π n, n € Z.

Let's assume. That for some n the number π n is the period

the function under consideration π n>0. Then sin|π n+x|=sin|x|

This implies that n must be both an even and an odd number, but this is impossible. Therefore, this function is not periodic.

Task 5. Check if the function is periodic

f(x)=

Let T be the period of f, then

, hence sinT=0, Т=π n, n € Z. Let us assume that for some n the number π n is indeed the period of this function. Then the number 2π n will be the period

Since the numerators are equal, their denominators are also equal, therefore

This means that the function f is not periodic.

Work in groups.

Tasks for group 1.

Tasks for group 2.

Check if the function f is periodic and find its fundamental period (if it exists).

f(x)=cos(2x)+2sin(2x)

Tasks for group 3.

At the end of their work, the groups present their solutions.

VI. Summing up the lesson.

Reflection.

The teacher gives students cards with drawings and asks them to color part of the first drawing in accordance with the extent to which they think they have mastered the methods of studying a function for periodicity, and in part of the second drawing - in accordance with their contribution to the work in the lesson.

VII. Homework

1). Check if the function f is periodic and find its fundamental period (if it exists)

b). f(x)=x 2 -2x+4

c). f(x)=2tg(3x+5)

2). The function y=f(x) has a period T=2 and f(x)=x 2 +2x for x € [-2; 0]. Find the value of the expression -2f(-3)-4f(3.5)

Literature/

1. Mordkovich A.G. Algebra and beginnings of analysis with in-depth study.
2. Mathematics. Preparation for the Unified State Exam. Ed. Lysenko F.F., Kulabukhova S.Yu.
3. Sheremeteva T.G. , Tarasova E.A. Algebra and beginning analysis for grades 10-11.

From school mathematics lessons, everyone remembers a sine graph stretching into the distance in uniform waves. Many other functions have a similar property - repeating at a certain interval. They are called periodic. Periodicity is a very significant quality of a function, often found in different tasks. Consequently, it is beneficial to be able to determine whether a function is periodic.

Instructions

1. If F(x) is a function of argument x, then it is called periodic if there is a number T such that for every x F(x + T) = F(x). This number T is called the period of the function. There can be several periods. Let's say that the function F = const takes the same value for all values ​​of the argument, and therefore any number can be considered its period. Traditionally, mathematics is concerned with the minimum non-zero period of a function. For brevity, it is called the primitive period.

2. A typical example of periodic functions is trigonometric: sine, cosine and tangent. Their period is identical and equal to 2?, that is, sin(x) = sin(x + 2?) = sin(x + 4?) and so on. However, of course, trigonometric functions are not exclusively periodic.

3. Regarding primitive, basic functions, the only method to establish their periodicity or non-periodicity is calculations. But for difficult functions there are already several primitive rules.

4. If F(x) is a periodic function with period T, and a derivative is defined for it, then this derivative f(x) = F?(x) is also a periodic function with period T. The value of the derivative at point x is equal to the tangent of the tangent angle the graph of its antiderivative at this point to the x-axis, and since the antiderivative is periodically repeated, the derivative must also be repeated. Let's say the derivative of the function sin(x) is equal to cos(x), and it is periodic. Taking the derivative of cos(x) gives you –sin(x). Periodicity remains constant. However, the opposite is not always true. Thus, the function f(x) = const is periodic, but its antiderivative F(x) = const*x + C is not.

5. If F(x) is a periodic function with period T, then G(x) = a*F(kx + b), where a, b, and k are constants and k is not equal to zero - is also a periodic function, and its period is T/k. Let's say sin(2x) is a periodic function, and its period is equal to?. This can be visually represented as follows: by multiplying x by any number, you seem to compress the graph of the function horizontally exactly that many times

6. If F1(x) and F2(x) are periodic functions, and their periods are equal to T1 and T2, respectively, then the sum of these functions can also be periodic. However, its period will not be an easy sum of periods T1 and T2. If the result of division T1/T2 is a reasonable number, then the sum of the functions is periodic, and its period is equal to the least universal multiple (LCM) of the periods T1 and T2. Let’s say, if the period of the first function is 12, and the period of the 2nd is 15, then the period of their sum will be equal to LCM (12, 15) = 60. This can be visually represented as follows: functions come with different “step widths,” but if the ratio their widths are meaningful, then sooner or later (or rather, precisely through the LCM of steps), they will become equal again, and their sum will begin the new period.

7. However, if the ratio of periods is irrational, then the total function will not be periodic at all. Let's say let F1(x) = x mod 2 (the remainder of dividing x by 2), and F2(x) = sin(x). T1 here will be equal to 2, and T2 will be equal to 2?. Is the period ratio equal? - an irrational number. Consequently, the function sin(x) + x mod 2 is not periodic.

Many mathematical functions have one specific feature that makes them easier to construct - this is periodicity, that is, the repeatability of the graph on a coordinate grid at equal intervals.

Instructions

1. The most well-known periodic functions in mathematics are the sine and cosine. These functions have a wave-like nature and a pivot period equal to 2P. Also a special case of a periodic function is f(x)=const. Any number fits into position x; this function does not have a main period, because it is a straight line.

2. In general, a function is periodic if there is an integer N that is non-zero and satisfies the rule f(x)=f(x+N), thus ensuring repeatability. The period of a function is the smallest number N, but not zero. That is, say, the function sin x is equal to the function sin (x+2ПN), where N=±1, ±2, etc.

3. Occasionally, a function may have a multiplier (say, sin 2x), one that will increase or decrease the period of the function. In order to detect the period by graphics, you need to determine the extrema of the function - the highest and lowest points of the function graph. Because sine and cosine waves have a wave-like nature, this is quite easy to do. From these points, construct perpendicular straight lines until they intersect with the X axis.

4. The distance from the upper extremum to the lower one will be half the period of the function. It is more convenient for everyone to calculate the period from the intersection of the graph with the Y axis and, accordingly, the zero mark on the x axis. After this, you need to multiply the resulting value by two and get the pivot period of the function.

5. To make it easier to plot sine and cosine curves, you need to note that if a function has an integer value, then its period will lengthen (that is, 2P must be multiplied by this indicator) and the graph will look more soft and smooth; and if the number is fractional, on the contrary, it will decrease and the graph will become more “sharp”, jump-like in appearance.

Video on the topic

From school mathematics lessons, everyone remembers a sine graph stretching into the distance in uniform waves. Many other functions have a similar property - repeating after a certain interval. They are called periodic. Periodicity is a very important property of a function, often encountered in various tasks. Therefore, it is useful to be able to determine whether a function is periodic.

Instructions

• If F(x) is a function of the argument x, then it is called periodic if there is a number T such that for any x F(x + T) = F(x). This number T is called the period of the function. There can be several periods. For example, the function F = const takes the same value for any value of the argument, and therefore any number can be considered its period. Mathematicians are usually interested in the smallest non-zero period of a function. For brevity, it is simply called a period.
• A classic example of periodic functions is trigonometric: sine, cosine and tangent. Their period is the same and equal to 2π, that is, sin(x) = sin(x + 2π) = sin(x + 4π) and so on. However, of course, trigonometric functions are not the only periodic ones.
• For simple, basic functions, the only way to determine whether they are periodic or non-periodic is through calculation. But for complex functions there are already several simple rules.
• If F(x) is a periodic function with period T, and a derivative is defined for it, then this derivative f(x) = F′(x) is also a periodic function with period T. After all, the value of the derivative at point x is equal to the tangent of the tangent angle graph its antiderivative at this point to the x-axis, and since the antiderivative is periodically repeated, the derivative must also be repeated. For example, the derivative of the function sin(x) is equal to cos(x), and it is periodic. Taking the derivative of cos(x) gives you –sin(x). The frequency remains unchanged. However, the opposite is not always true. Thus, the function f(x) = const is periodic, but its antiderivative F(x) = const*x + C is not.
• If F(x) is a periodic function with period T, then G(x) = a*F(kx + b), where a, b, and k are constants and k is not equal to zero - is also a periodic function, and its period is T/k. For example, sin(2x) is a periodic function, and its period is π. This can be visually represented as follows: by multiplying x by some number, you seem to compress the graph of the function horizontally exactly that many times
• If F1(x) and F2(x) are periodic functions, and their periods are equal to T1 and T2, respectively, then the sum of these functions can also be periodic. However, its period will not be a simple sum of periods T1 and T2. If the result of division T1/T2 is a rational number, then the sum of the functions is periodic, and its period is equal to the least common multiple (LCM) of the periods T1 and T2. For example, if the period of the first function is 12, and the period of the second is 15, then the period of their sum will be equal to LCM (12, 15) = 60. This can be visually represented as follows: the functions come with different “step widths,” but if the ratio of their widths rationally, then sooner or later (or rather, precisely through the LCM of steps), they will become equal again, and their sum will begin a new period.
• However, if the ratio of periods is irrational, then the total function will not be periodic at all. For example, let F1(x) = x mod 2 (the remainder when x is divided by 2), and F2(x) = sin(x). T1 here will be equal to 2, and T2 will be equal to 2π. The ratio of periods is equal to π - an irrational number. Therefore, the function sin(x) + x mod 2 is not periodic.