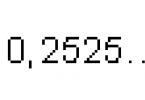This is a creative task for a master class in computer science for schoolchildren at FEFU.
The purpose of the task is to find out how the trajectory of the body will change if air resistance is taken into account. It is also necessary to answer the question of whether the flight distance will still reach its maximum value at a throwing angle of 45°, if air resistance is taken into account.

The “Analytical Research” section outlines the theory. This section can be skipped, but it should be mostly clear to you because... O you learned most of this in school.
The "Numerical Study" section contains a description of the algorithm that must be implemented on a computer. The algorithm is simple and concise, so everyone should be able to do it.

Analytical research

Let's introduce a rectangular coordinate system as shown in the figure. At the initial moment of time a body of mass m is located at the origin. The free fall acceleration vector is directed vertically downward and has coordinates (0, - g).
- initial velocity vector. Let's expand this vector into its basis: . Here , where is the magnitude of the velocity vector, is the throwing angle.

Let's write down Newton's second law: .
Acceleration at each moment of time is the (instantaneous) rate of change of speed, that is, the derivative of speed with respect to time: .

Therefore, Newton's 2nd law can be rewritten as follows:
, where is the resultant of all forces acting on the body.
Since the force of gravity and the force of air resistance act on the body, then
.

We will consider three cases:
1) The air resistance force is 0: .
2) The air resistance force is oppositely directed with the velocity vector, and its magnitude is proportional to the speed: .
3) The air resistance force is oppositely directed with the velocity vector, and its magnitude is proportional to the square of the velocity: .

Let's first consider the 1st case.
In this case , or .


It follows that (uniformly accelerated motion).
Because ( r- radius vector), then .
From here .
This formula is nothing more than the familiar formula for the law of motion of a body during uniformly accelerated motion.
Since then .
Considering that both , we obtain scalar equalities from the last vector equality:

Let us analyze the resulting formulas.
Let's find flight time bodies. Equating y to zero, we get

Range of flight equal to the coordinate value x at a point in time t 0:

From this formula it follows that the maximum flight range is achieved at .
Now let's find body tractor equation. To do this, we express t through x

And let’s substitute the resulting expression for t into equality for y.

Resulting function y(x) is a quadratic function, its graph is a parabola, the branches of which are directed downwards.
The movement of a body thrown at an angle to the horizon (without taking into account air resistance) is described in this video.

Now consider the second case: .

The second law takes the form ,
from here .
Let us write this equality in scalar form:

We got two linear differential equations.
The first equation has a solution

This can be verified by substituting this function into the equation for v x and to the initial condition .
Here e = 2.718281828459... is Euler's number.
The second equation has a solution

Because , , then in the presence of air resistance the movement of the body tends to be uniform, in contrast to case 1, when the speed increases without limit.
The following video says that the skydiver first moves at an accelerated pace, and then begins to move evenly (even before the parachute opens).

Let's find expressions for x And y.
Because x(0) = 0, y(0) = 0, then

It remains for us to consider case 3, when .
Newton's second law has the form
, or .
In scalar form, this equation looks like:

This system of nonlinear differential equations. This system cannot be solved explicitly, so it is necessary to use numerical simulation.

Numerical study

In the previous section we saw that in the first two cases the law of motion of a body can be obtained in explicit form. However, in the third case it is necessary to solve the problem numerically. Using numerical methods we will obtain only an approximate solution, but we will be quite satisfied with a small accuracy. (The number π or the square root of 2, by the way, cannot be written down absolutely precisely, so when calculating, they take a finite number of digits, and this is quite enough.)

We will consider the second case, when the force of air resistance is determined by the formula . Note that when k= 0 we get the first case.

Body speed obeys the following equations:

The acceleration components are written on the left sides of these equations .
Recall that acceleration is the (instantaneous) rate of change of velocity, that is, the derivative of velocity with respect to time.
The right-hand sides of the equations contain the velocity components. Thus, these equations show how the rate of change of velocity is related to speed.

Let's try to find solutions to these equations using numerical methods. To do this, we introduce on the time axis mesh: let's choose a number and consider moments of time of the form: .

Our task is to approximately calculate the values at grid nodes.

Let us replace the acceleration in the equations ( instantaneous speed speed changes) by average speed changes in speed, considering the movement of a body over a period of time:

Now let’s substitute the obtained approximations into our equations.

The resulting formulas allow us to calculate the values ​​of the functions at the next grid node, if the values ​​of these functions at the previous grid node are known.

Using the described method, we can obtain a table of approximate values ​​of the velocity components.

How to find the law of body motion, i.e. table of approximate coordinate values x(t), y(t)? Likewise!
We have

The value of vx[j] is equal to the value of the function, and the same for other arrays.
Now all that remains is to write a loop, inside which we will calculate vx using the already calculated value vx[j], and the same with the rest of the arrays. The cycle will be j from 1 to N.
Don't forget to initialize the initial values ​​vx, vy, x, y according to the formulas, x 0 = 0, y 0 = 0.

In Pascal and C, there are functions sin(x) and cos(x) for calculating sine and cosine. Note that these functions take an argument in radians.

You need to construct a graph of body movement during k= 0 and k> 0 and compare the resulting graphs. Graphs can be created in Excel.
Note that the calculation formulas are so simple that you can use only Excel for calculations and not even use a programming language.
However, in the future you will need to solve a problem in CATS, in which you need to calculate the time and range of a body's flight, where you cannot do without a programming language.

Please note that you can test your program and check your graphs by comparing the calculation results when k= 0 with the exact formulas given in the “Analytical study” section.

Experiment with your program. Make sure that if there is no air resistance ( k= 0) the maximum flight range at a fixed initial speed is achieved at an angle of 45°.
What about air resistance? At what angle is maximum flight range achieved?

The figure shows the trajectories of the body at v 0 = 10 m/s, α = 45°, g= 9.8 m/s 2, m= 1 kg, k= 0 and 1 obtained by numerical simulation at Δ t = 0,01.

You can familiarize yourself with the wonderful work of 10th graders from Troitsk, presented at the “Start in Science” conference in 2011. The work is devoted to modeling the movement of a tennis ball thrown at an angle to the horizon (taking into account air resistance). Both numerical modeling and full-scale experiment are used.

Thus, this creative task allows you to get acquainted with the methods of mathematical and numerical modeling, which are actively used in practice, but are little studied at school. For example, these methods were used in the implementation of nuclear and space projects in the USSR in the mid-20th century.

When studying mechanical motion in physics, after becoming familiar with the uniform and uniformly accelerated movement of objects, they move on to considering the movement of a body at an angle to the horizon. In this article we will study this issue in more detail.

What is the movement of a body at an angle to the horizontal?

This type of object movement occurs when a person throws a stone into the air, a cannon fires a cannonball, or a goalkeeper kicks a soccer ball away from the goal. All such cases are considered by the science of ballistics.

The noted type of movement of objects in the air occurs along a parabolic trajectory. In the general case, carrying out the corresponding calculations is not a simple matter, since it is necessary to take into account air resistance, rotation of the body during flight, rotation of the Earth around its axis and some other factors.

In this article we will not take into account all these factors, but will consider the issue from a purely theoretical point of view. Nevertheless, the resulting formulas describe the trajectories of bodies moving over short distances quite well.

Obtaining formulas for the type of movement under consideration

Let's bring the bodies to the horizon at an angle. In this case, we will take into account only one single force acting on a flying object - gravity. Since it acts vertically downward (parallel to and against the y-axis), then, considering the horizontal and vertical components of the movement, we can say that the first will have the character of uniform rectilinear movement. And the second - uniformly slow (uniformly accelerated) rectilinear movement with acceleration g. That is, the velocity components through the value v 0 (initial speed) and θ (angle of direction of body motion) will be written as follows:

v x = v 0 *cos(θ)

v y = v 0 *sin(θ)-g*t

The first formula (for v x) is always valid. As for the second, one nuance should be noted here: the minus sign is placed in front of the product g*t only if the vertical component v 0 *sin(θ) is directed upward. In most cases, this is what happens, however, if you throw a body from a height, pointing it down, then in the expression for v y you should put a “+” sign in front of g*t.

Having integrated the formulas for the velocity components over time, and taking into account the initial height h of the body’s flight, we obtain equations for the coordinates:

x = v 0 *cos(θ)*t

y = h+v 0 *sin(θ)*t-g*t 2 /2

Flight range calculation

When considering in physics the movement of a body towards the horizon at an angle useful for practical application, it turns out to be the calculation of flight range. Let's define it.

Since this movement is a uniform movement without acceleration, it is enough to substitute the flight time into it and get the desired result. Flight range is determined solely by movement along the x-axis (parallel to the horizon).

The time a body remains in the air can be calculated by setting the y coordinate to zero. We have:

0 = h+v 0 *sin(θ)*t-g*t 2 /2

We solve this quadratic equation through the discriminant, we get:

D = b 2 - 4*a*c = v 0 2 *sin 2 (θ) - 4*(-g/2)*h = v 0 2 *sin 2 (θ) + 2*g*h,

t = (-b±√D)/(2*a) = (-v 0 *sin(θ)±√(v 0 2 *sin 2 (θ) + 2*g*h))/(-2* g/2) =

= (v 0 *sin(θ)+√(v 0 2 *sin 2 (θ) + 2*g*h))/g.

In the last expression, one root with a minus sign is discarded due to its insignificant physical significance. Substituting the flight time t into the expression for x, we obtain the flight range l:

l = x = v 0 *cos(θ)*(v 0 *sin(θ)+√(v 0 2 *sin 2 (θ) + 2*g*h))/g.

The easiest way to analyze this expression is if the initial height is zero (h=0), then we get a simple formula:

l = v 0 2 *sin(2*θ)/g

This expression indicates that the maximum flight range can be obtained if the body is thrown at an angle of 45 o (sin(2*45 o) = m1).

Maximum lifting height

In addition to the flight distance, it is also useful to find the height above the ground that the body can rise to. Since this type of movement is described by a parabola, the branches of which are directed downwards, the maximum lift height is its extremum. The latter is calculated by solving the equation for the t derivative of y:

dy/dt = d(h+v 0 *sin(θ)*t-g*t 2 /2)/dt = v 0 *sin(θ)-gt=0 =>

=> t = v 0 *sin(θ)/g.

Substituting this time into the equation for y, we get:

y = h+v 0 *sin(θ)*v 0 *sin(θ)/g-g*(v 0 *sin(θ)/g) 2 /2 = h + v 0 2 *sin 2 (θ)/( 2*g).

This expression indicates that the body will rise to its maximum height if it is thrown vertically upward (sin 2 (90 o) = 1).

If a body is thrown at an angle to the horizon, then in flight it is acted upon by the force of gravity and the force of air resistance. If the resistance force is neglected, then the only force left is gravity. Therefore, due to Newton’s 2nd law, the body moves with acceleration equal to the acceleration of gravity; projections of acceleration onto the coordinate axes ax = 0, ay = - g.

Figure 1. Kinematic characteristics of a body thrown at an angle to the horizontal

Any complex movement of a material point can be represented as a superposition of independent movements along the coordinate axes, and in the direction of different axes the type of movement may differ. In our case, the motion of a flying body can be represented as the superposition of two independent motions: uniform motion along the horizontal axis (X-axis) and uniformly accelerated motion along the vertical axis (Y-axis) (Fig. 1).

The body's velocity projections therefore change with time as follows:

where $v_0$ is the initial speed, $(\mathbf \alpha )$ is the throwing angle.

With our choice of origin, the initial coordinates (Fig. 1) are $x_0=y_0=0$. Then we get:

(1)

Let's analyze formulas (1). Let us determine the time of movement of the thrown body. To do this, let's set the y coordinate equal to zero, because at the moment of landing the height of the body is zero. From here we get for the flight time:

The second time value at which the height is zero is zero, which corresponds to the moment of throwing, i.e. this value also has a physical meaning.

We obtain the flight range from the first formula (1). The flight range is the value of the x coordinate at the end of the flight, i.e. at time equal to $t_0$. Substituting value (2) into the first formula (1), we get:

From this formula it can be seen that the greatest flight range is achieved at a throwing angle of 45 degrees.

The maximum lifting height of the thrown body can be obtained from the second formula (1). To do this, you need to substitute a time value equal to half the flight time (2) into this formula, because It is at the midpoint of the trajectory that the flight altitude is maximum. Carrying out calculations, we get

From equations (1) one can obtain the equation of the body’s trajectory, i.e. an equation relating the x and y coordinates of a body during motion. To do this, you need to express time from the first equation (1):

and substitute it into the second equation. Then we get:

This equation is the motion trajectory equation. It can be seen that this is the equation of a parabola with its branches down, as indicated by the “-” sign in front of the quadratic term. It should be borne in mind that the throwing angle $\alpha $ and its functions are simply constants here, i.e. constant numbers.

A body is thrown with speed v0 at an angle $(\mathbf \alpha )$ to the horizon. Flight time $t = 2 s$. To what height Hmax will the body rise?

$$t_B = 2 s$$ $$H_max - ?$$

The law of body motion has the form:

$$\left\( \begin(array)(c) x=v_(0x)t \\ y=v_(0y)t-\frac(gt^2)(2) \end(array) \right.$ $

The initial velocity vector forms an angle $(\mathbf \alpha )$ with the OX axis. Hence,

\ \ \

A stone is thrown from the top of a mountain at an angle = 30$()^\circ$ to the horizon with an initial speed of $v_0 = 6 m/s$. Inclined plane angle = 30$()^\circ$. At what distance from the point of throwing will the stone fall?

$$ \alpha =30()^\circ$$ $$v_0=6\ m/s$$ $$S - ?$$

Let's place the origin of coordinates at the throwing point, OX - along the inclined plane downwards, OY - perpendicular to the inclined plane upwards. Kinematic characteristics of movement:

Law of motion:

$$\left\( \begin(array)(c) x=v_0t(cos 2\alpha +g\frac(t^2)(2)(sin \alpha \ )\ ) \\ y=v_0t(sin 2 \alpha \ )-\frac(gt^2)(2)(cos \alpha \ ) \end(array) \right.$$ \

Substituting the resulting value $t_В$, we find $S$:

The maximum range of a stone fired from a stationary catapult is S = 22.5 m. Find the maximum possible range of a stone fired from the same catapult mounted on a platform moving horizontally at a constant speed v = 15.0 m/s. Ignore air resistance, calculate free fall acceleration g = 10.0 m/s 2.

Solution: It is well known that the maximum flight range of a body thrown at an angle to the horizontal is achieved at an angle of departure equal to 45° and is determined by the formula:

Let us now consider the flight of a stone released from a moving catapult. Let us introduce a coordinate system whose axes are: X- directed horizontally, and Y— vertically. The origin of coordinates is compatible with the position of the catapult at the moment the stone is released.

To calculate the speed vector of the stone, it is necessary to take into account the horizontal speed of the catapult v = v o. Let's say that a catapult throws a stone at an angle α to the horizon. Then the components of the initial velocity of the stone in our coordinate system can be written as:

Substituting this expression into the first equation of system (3), we obtain the flight range of the stone:

Secondly, it does not at all follow from (5) that S 1 will be maximum at α = 45°(this is true for (6), when v=0).

Proposing this problem for the Republican Olympiad, the authors were convinced that nine-tenths of the participants would receive formula (5) and then substitute the value into it α = 45°. However, to our regret, we were mistaken: not a single Olympian doubted that the maximum flight range is always (!) achieved at an angle of departure equal to 45°. This well-known fact has limited applicability: it is only true if:

a) do not take into account air resistance;
b) the take-off point and the fall point are at the same level;
c) the projectile is stationary.

Let's return to solving the problem. So we need to find the angle value α , at which S 1 determined by formula (5), is maximum. You can, of course, find the extremum of the function using the apparatus of differential calculus: find the derivative, set it equal to zero and, having solved the resulting equation, find the desired value α . However, given that the problem was proposed to 9th grade students, we will give its geometric solution. Let us take advantage of the fact that v = v o = 15 m/s.

Let's arrange the vectors v And v o as shown in fig. Since their lengths are equal, a circle with center at point O can be described around them. Then the length of the segment A.C. equal to v o + v o cos α(this is vxo), and the length of the segment B.C. equal to v o sin α(This vyo). Their product is equal to twice the area of ​​the triangle ABC, or area of ​​the triangle ABB 1.

Please note that it is the product that is included in the expression for flight range (5). In other words, the flight range is equal to the product of the area ΔАВВ 1 by a constant factor 2/g.

Now let’s ask ourselves: which of the triangles inscribed in a given circle has the maximum area? Naturally correct! Therefore, the desired value of the angle α = 60°.

Vector AB there is a vector of the total initial speed of the stone, it is directed at an angle 30° to the horizon (again, not at all 45°).

Thus, the final solution to the problem follows from formula (5), into which we should substitute α = 60°.