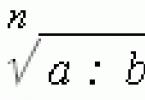
У цій статті ви знайдете властивості бісектриси та медіани трикутника, які можуть бути корисними при вирішенні завдань.

Бісектриси.

1. Точка перетину бісектрис трикутника є центром вписаного в трикутник кола.

Доведення.

Справді, точки, що лежать на бісектрисі кута, рівновіддалені від сторін кута. Отже, точка перетину бісектрис рівновіддалена від усіх сторін трикутника, тобто є центром вписаного кола.

2. Бісектриса трикутника ділить протилежну сторону на відрізки, пропорційні прилеглим сторонам:

Доведення.

Зробимо додаткові побудови. Проведемо через точку пряму, паралельну

Точка перетину прямої та прямої:

∠1=∠2, оскільки - бісектриса ∠

∠2=∠3 як навхрест лежачі, оскільки за побудовою.

Отже, ∠1=∠3 та трикутник - рівнобедрений, і .

отже,

3. Довжина бісектриси обчислюється за такими формулами:

Доведемо другу формулу.

Введемо позначення:

Прирівняємо вирази для площі трикутника:

4. Нехай О-центр вписаного кола, -бісектриса кута трикутника :

Тоді виконується співвідношення:

Доведення:

Розглянемо трикутник:

Бісектриса кута , отже, за властивістю бісектриси трикутника

Нехай тоді

Виразимо. За властивістю бісектриси трикутника:

Звідси

Бісектрису трикутника в деяких завданнях зручно продовжити до перетину з описаним колом.

Лемма про трилисник.

Даний трикутник. Крапка - точка перетину бісектриси кута з описаним біля трикутника колом. Нехай - центр вписаного в трикутник кола. Тоді

Доведення.

Вписані кути, що спираються на рівні дуги, рівні. Зазначимо рівні вписані кути:

Звідси.

Центр вписаного кола, тому -біссектриса кута.

З трикутника

Тоді із трикутника

Отримали.

Тобто трикутник – рівнобедрений.

Звідси.

Довели, що

Доведемо формулу (1) із п. 3:

Доведення:

Продовжимо бісектрису до перетину з описаним колом. Розглянемо трикутники та . Зазначимо рівні кути:

Трикутник подібний до трикутника по двох кутах. Звідси:

За якістю відрізків хорд, що перетинаються

Підставимо (3) у (2) і скористаємося (4):

Виразимо довжини відрізків, на які бісектриса ділить сторону трикутника через довжини сторін трикутника. Введемо позначення:

Отримаємо систему:

Медіани.

1. Медіани трикутника діляться точкою перетину щодо 2:1, рахуючи від вершини:

2. Нехай - точка всередині трикутника така, що виконується співвідношення: , то - точка перетину медіан трикутника.

Доведення.

Доведемо допоміжну теорему.

Лемма.

Для довільної точки всередині трикутника виконується співвідношення:

Опустимо з крапок і перпендикуляри на :

З подоби трикутників і отримуємо:

Якщо ми розглянемо трикутники і із загальною основою , То отримаємо співвідношення:

Аналогічно отримаємо

Склавши ці рівності отримаємо:

Використовуємо цю лему для підтвердження твердження 2.

Якщо виконується рівність (1) , то виконується рівність (2) і з леми випливає, що в рівності (2) кожен дріб дорівнює .

Доведемо, що у цьому випадку відрізки є медіаном.

Якщо , то отримуємо . Проведемо через точку прямі, паралельні і розглянемо дві пари подібних трикутників: і :

Звідси отримуємо

З подоби трикутників отримуємо, тобто точка-середина відрізка. Звідси.

Отже, - медіана трикутника.

3. Медіани трикутника, перетинаючи, розбивають його на 6 рівновеликих трикутників.

Доведення.

Доведемо, що

так як ,

так як ,

Отже,

Висоти.

1. Прямі, що містять висоти трикутника, перетинаються в одній точці. У разі гострокутного трикутника в одній точці перетинаються самі висоти.

2. Точка перетину висот трикутника має таку властивість: сума квадрата відстані від вершини трикутника і квадрата протилежної сторони однакова для будь-якої вершини:

Доведення.

Доведемо першу частину рівності:

Перепишемо його у вигляді:

За теоремою Піфагора: (з трикутників і )

(з трикутника)

(з трикутника)

Підставимо ці вирази в (1), отримаємо:

Розкриємо дужки, отримаємо:

Здобули тотожність. Друга частина рівності доводиться аналогічно.

3. Якщо описати навколо трикутника коло і продовжити висоти трикутника до перетину з цим колом,

то для будь-якої висоти трикутника відстань від основи висоти до точки перетину продовження висоти з колом дорівнює відстані від основи висоти до точки перетину висот:

Або так: Точки, симетричні точці перетину висот трикутника щодо сторін трикутника, лежать на описаному біля трикутника колі.

Доведення.

Доведемо, що .

Для цього розглянемо трикутники і , і доведемо, що :

Скористаємося ознакою рівності трикутників з обох боків і двом прилеглим кутам. - Спільна сторона. Доведемо рівність двох кутів.

Доведемо, що ∠ ∠

Нехай ∠, тоді з трикутника отримаємо, що

∠. Отже, з трикутника отримаємо, що

Але ∠ і ∠ спираються однією дугу , отже, ∠ ∠ ∠

Аналогічно отримуємо, що ∠ ∠

4. У трикутнику точки і - основи висот, проведених з вершин і . Довести, що трикутник подібний до трикутника і коефіцієнт подібності дорівнює .

Доведення:

Центр кола, описаного біля прямокутного трикутника, лежить у середині гіпотенузи. . Крапка лежить на цьому колі, оскільки - гіпотенуза прямокутного трикутника:

Як вписані кути, що спираються однією дугу.

з трикутника:

Звідси. Кут - загальний кут трикутників і . Отже, трикутник подібний до трикутника . Коефіцієнт подібності дорівнює відношенню подібних сторін, тобто сторін, які лежать проти рівних кутів:

Теорема Чеви

Нехай у трикутнику

Відрізки перетинаються в одній точці в тому і лише тому випадку, якщо

Доведення.

Доведемо, що якщо відрізки перетинаються в одній точці, співвідношення (1) виконується.

Легко перевірити, що якщо , то виконується

Застосуємо цю властивість пропорції:

Аналогічно:

Теорему Чеви можна записати в такому вигляді:

Якщо відрізки перетинаються в одній точці, виконується співвідношення:

Щоб довести теорему Чеви у формі синусівдостатньо в другу частину рівності (2) замість площ трикутників підставити для площі кожного трикутника формулу .

З лекцій Агаханова Назара Хангельдійовича та Володимира Вікторовича Трушкова, КПК МФТІ.

Властивості

• Медіани трикутника перетинаються в одній точці, яка називається центроїдом, і діляться цією точкою на дві частини щодо 2:1, рахуючи від вершини.
• Трикутник ділиться трьома медіанами на шість рівновеликих трикутників.
• Більшій стороні трикутника відповідає менша медіана.
• З векторів, що утворюють медіани, можна скласти трикутник.
• При афінних перетвореннях медіана перетворюється на медіану.
• Медіана трикутника ділить його на дві рівновеликі частини.

Формули

• Формула медіани через сторони (виводиться через теорему Стюарта або добудовою до паралелограма та використанням рівності у паралелограмі суми квадратів сторін та суми квадратів діагоналей):

де m c - медіана до сторони c; a, b, c - сторони трикутника, тому сума квадратів медіан довільного трикутника завжди в 4/3 рази менша від суми квадратів його сторін.

• Формула сторони через медіани:

, де медіани до відповідних сторін трикутника - сторони трикутника.

Якщо дві медіани перпендикулярні, то сума квадратів сторін, на які вони опущені, у 5 разів більша за квадрат третьої сторони.

Мнемонічне правило

Медіана-мавпа,
у якої пильне око,
стрибне точно в середину
сторони проти вершини,
де зараз.

Примітки

Див. також

Посилання

Wikimedia Foundation. 2010 .

Дивитись що таке "Медіана трикутника" в інших словниках:

Медіана: Медіана трикутника в планіметрії, відрізок, що з'єднує вершину трикутника з серединою протилежної сторони в статистиці медіаною, називається значення сукупності, що ділить ранжований ряд даних навпіл Медіана (статистика).

Медіана: Медіана трикутника в планіметрії, відрізок, що з'єднує вершину трикутника з серединою протилежної сторони Медіана (статистика) квантиль 0.5 Медіана (траса) середня лінія траси, проведена між правим та лівим …

Трикутник та його медіани. Медіана трикутника ― відрізок усередині трикутника, що з'єднує вершину трикутника із серединою протилежної сторони, а також пряма, що містить цей відрізок. Зміст 1 Властивості 2 Формули … Вікіпедія

Лінія, що з'єднує вершину трикутника із серединою його основи. Повний словник іншомовних слів, що увійшли у вжиток у російській мові. Попов М., 1907. Медіана (лат. Mediana середня) 1) геол. відрізок, що з'єднує вершину трикутника з ... Словник іноземних слів російської мови

Медіана (від латинського mediana середня) у геометрії, відрізок, що з'єднує одну з вершин трикутника із серединою протилежної сторони. Три М. трикутника перетинаються в одній точці, яку іноді називають центром тяжіння трикутника, так … Велика Радянська Енциклопедія

Трикутника пряма (або її відрізок усередині трикутника), що з'єднує вершину трикутника із серединою протилежної сторони. Три М. трикутника перетинаються в одній точці, яка називається центром тяжкості трикутника, центроїдом, або ... ... Математична енциклопедія

- (Від лат. Mediana середня) відрізок, що з'єднує вершину трикутника з серединою протилежної сторони … Великий Енциклопедичний словник

МЕДІАНА, медіани, жін. (Лат. Mediana, букв. Середня). 1. Пряма лінія, проведена від вершини трикутника до середини протилежної сторони (мат.). 2. У статистиці для багатьох даних величина, що має тим властивістю, що число даних, … Тлумачний словник Ушакова

МЕДІАНА, ы, жен. В математиці: відрізок прямої лінії, що з'єднує вершину трикутника із серединою протилежної сторони. Тлумачний словник Ожегова. С.І. Ожегов, Н.Ю. Шведова. 1949 1992 … Тлумачний словник Ожегова

МЕДІАНА (від лат. mediana середня), відрізок, що з'єднує вершину трикутника з серединою протилежної сторони. Енциклопедичний словник

Властивості хорд

1. Діаметр (радіус), перпендикулярний до хорди, ділить цю хорду і обидві дуги, що нею стягуються навпіл. Вірна і зворотна теорема: якщо діаметр (радіус) ділить навпіл хорду, він перпендикулярний цій хорді.

2. Дуги, укладені між паралельними хордами, рівні.

3. Якщо дві хорди кола, ABі CDперетинаються у точці M, то добуток відрізків однієї хорди дорівнює добутку відрізків іншої хорди: AM MB = CM MD.

Властивості кола

1. Пряма може мати з колом загальних точок; мати з колом одну загальну точку ( дотична); мати з нею дві спільні точки ( січуча).

2. Через три точки, що не лежать на одній прямій, можна провести коло, і до того ж лише одну.

3. Точка торкання двох кіл лежить на лінії, що з'єднує їх центри.

Теорема про дотичну та січну

Якщо з точки, що лежить поза коло, проведено дотичну та січні, то квадрат довжини дотичної дорівнює добутку січеної на її зовнішню частину: MC 2 = MA MB.

Теорема про січучих

Якщо з точки, що лежить поза коло, проведено дві січучі, то добуток однієї січе на її зовнішню частину дорівнює твору іншої січе на її зовнішню частину. MA MB = MC MD.

Кути в колі

Центральнимкутом у колі називається плоский кут з вершиною у її центрі.

Кут, вершина якого лежить на колі, а сторони перетинають це коло, називається вписаним кутом.

Будь-які дві точки кола поділяють її на дві частини. Кожна з цих частин називається дугоюкола. Мірою дуги може бути міра відповідного їй центрального кута.

Дуга називається півколо,якщо відрізок, що з'єднує кінці, є діаметром.

Властивості кутів, пов'язаних з колом

1. Вписаний кут або дорівнює половині відповідного йому центрального кута, або доповнює половину цього кута до 180 °.

2. Кути, вписані в одне коло і спираються на ту саму дугу, рівні.

3. Вписаний кут, що спирається на діаметр, дорівнює 90 °.

5. Кут, утворений дотичною до кола та січної, проведеної через точку торкання, дорівнює половині дуги, укладеної між його сторонами.

Довжини та площі

1. Довжина кола Cрадіусу Rобчислюється за такою формулою: C = 2 R.

2. Площа Sкола радіусу Rобчислюється за такою формулою: S = R 2.

3. Довжина дуги кола Lрадіусу Rз центральним кутом, виміряним у радіанах, обчислюється за формулою: L = R .

4. Площа Sсектора радіусу Rз центральним кутом у радіан обчислюється за формулою: S = R 2 .

Вписані та описані кола

Окружність та трикутник

· Центр вписаного кола - точка перетину бісектрис трикутника, її радіус rобчислюється за такою формулою:

r =, де S- площа трикутника, а - напівпериметр;

· Центр описаного кола - точка перетину серединних перпендикулярів, її радіус R обчислюється за формулою:

R = , R =;

· Центр описаної біля прямокутного трикутника кола лежить на середині гіпотенузи;

· Центр описаного та вписаного кіл трикутника збігаються тільки в тому випадку, коли цей трикутник - правильний.

Коло та чотирикутники

· У опуклого чотирикутника можна описати коло тоді і тільки тоді, коли сума його внутрішніх протилежних кутів дорівнює 180 °:

180 °;

у чотирикутник можна вписати коло тоді і лише тоді, коли в нього рівні суми протилежних сторін a + c = b + d;

навколо паралелограма можна описати коло тоді й лише тоді, коли він є прямокутником;

· біля трапеції можна описати коло тоді й лише тоді, коли ця трапеція - рівнобедрена; центр кола лежить на перетині осі симетрії трапеції із серединним перпендикуляром до бокової сторони;

· У паралелограм можна вписати коло тоді і лише тоді, коли він є ромбом.

Трикутники

Властивості медіан трикутника

1. Медіана розбиває трикутник на два трикутники однакової площі.

2. Медіани трикутника перетинаються в одній точці, яка ділить кожну з них щодо 2:1, рахуючи від вершини. Ця точка називається центром тяжіннятрикутник.

3. Весь трикутник поділяється своїми медіанами на шість рівновеликих трикутників.

Властивості бісектрис трикутника

1. Бісектриса кута – це геометричне місце точок, рівновіддалених від сторін цього кута.

2. Бісектриса внутрішнього кута трикутника ділить протилежну сторону на відрізки, пропорційні прилеглим сторонам: .

3. Точка перетину бісектрис трикутника є центром кола, вписаного в цей трикутник.

Властивості висот трикутника

1. У прямокутному трикутнику висота, проведена з вершини прямого кута, розбиває його на два трикутники, подібні до вихідного.

2. У гострокутному трикутнику дві його висоти відсікають від нього подібні трикутники.

Існує теорема про те, що медіани трикутника перетинаються в одній точці, і ця точка ділить кожну медіану щодо 2: 1де 2 відповідає відрізку від вершини, з якої проведена медіана, до точки перетину медіан, а 1 відповідає відрізку від точки перетину медіан до середини сторони, до якої проведена медіана.

Щоб довести цю теорему, розглянемо трикутник ABC із медіанами AE, BF, CD. Тобто точки D, E, F ділять навпіл сторони AB, BC, CA відповідно.
Нам не відомо, чи всі медіани перетинаються в одній точці (це ще потрібно довести). Однак будь-які дві медіани перетнуться в одній точці, тому що не можуть бути паралельні. Нехай медіани AE та BF перетинаються у точці O.

Медіана BF ділить медіану AE на два відрізки AO та EO. Проведемо через точку E пряму, паралельну до BF. Ця пряма перетне бік AC у певній точці L. Також проведемо через середину відрізка AB (точку D) ще одну паралельну до BF пряму. Вона перетне AC в точці K.

Згідно з теоремою Фалеса, якщо на одній стороні кута від його вершини відкласти послідовно рівні відрізки і провести через кінці цих відрізків паралельні прямі, що перетинають іншу сторону кута, ці паралельні прямі відсічуть на другій стороні кута також рівні між собою відрізки.

Подивимося на кут BCA цього трикутника. Відрізки BE та EC рівні між собою, прямі BF та EL паралельні один одному. Тоді згідно з теоремою Фалеса CL = LF.
Якщо ж подивитися на кут BAC, тому що AD = BD та DK || BF, AK = KF.

Так як відрізки AF і CF рівні між собою (т.к. їх утворює медіана) і кожен з них ділиться на два рівні відрізки, то всі чотири відрізки сторони AC рівні між собою: AK = KF = FL = LC.

Розглянемо кут EAC. Через кінці трьох рівних відрізків сторони AC проведено паралельні прямі. Отже, вони відсікають на боці AE рівні між собою відрізки. Відрізок AO містить два таких відрізка, а EO тільки один. Таким чином, ми довели, що як мінімум одна медіана трикутника точкою перетину з іншою медіаною ділиться на два відрізки, довжини яких співвідносяться як 2:1.

Тепер розглянемо перетин медіани AE з медіаною CD. Нехай вони перетинаються у точці P.

Аналогічно попередньому доводиться, що паралельні прямі FM, CD, EN ділять сторону AB на рівні відрізки. У свою чергу вони ж ділять AE на три рівні відрізки. Причому від вершини A до перетину медіан два такі відрізки, а після - один.

Один і той же відрізок не можна розділити на три рівні частини так, щоб при одному варіанті поділу вони були одного розміру, а при іншому - іншого. Тому точки O та P повинні збігатися. Це означає, що всі три медіани трикутники перетинаються в одній точці.

Щоб довести, що інші дві медіани діляться точкою перетину у співвідношенні 2: 1, можна аналогічно попередньому провести паралельні прямі до сторін AB і BC.

Медіана – одна з основних ліній трикутника. Цей відрізок і пряма, на якій він лежить, з'єднує крапку на чолі кута трикутника з серединою протилежної сторони цієї фігури. У рівносторонньому трикутнику медіана є також бісектрисою та висотою.

Властивість медіани, яка суттєво полегшить вирішення багатьох завдань, полягає в наступному: якщо в трикутнику провести медіани з кожного кута, всі вони, перетинаючи в одній точці, буде ділитися у співвідношенні 2:1. Співвідношення слід відраховувати від вершини кута.

Медіана має властивість поділяти все порівну. Наприклад, будь-яка медіана ділить трикутник на два інших, рівних за своєю площею. А якщо провести всі три медіани, то у великому трикутнику вийде 6 маленьких, також рівних за площею. Такі постаті (з однаковою площею) називаються рівновеликими.

Бісектриса

Бісектриса є промінь, який починається у вершині кута і ділить цей же кут навпіл. Крапки, що лежать на даному промені, рівновіддалені від сторін кута. Властивості бісектриси добре допомагають у вирішенні завдань, пов'язаних із трикутниками.

У трикутнику бісектриси називають відрізок, який лежить на промені бісектриси кута і з'єднує вершину з протилежною стороною. Точка перетину зі стороною ділить її на відрізки, відношення яких дорівнює відношенню прилеглих до них сторін.

Якщо в трикутник вписати коло, то його центр збігатиметься з точкою перетину всіх бісектрис цього трикутника. Ця властивість має відображення і в стереометрії – там роль трикутника грає піраміда, а кола – куля.

Висота

Також як медіана та бісектриса, висота в трикутнику в першу чергу пов'язують вершину кута та протилежну сторону. Це зв'язок відбувається у наступному: висота – це перпендикуляр, проведений з вершини, до прямої, що містить у собі протилежну сторону.

Якщо висота проведена у прямокутному трикутнику, то, торкаючись протилежної сторони, вона ділить весь трикутник на два інших, які у свою чергу подібні до першого.

Нерідко поняття перпендикуляра застосовується у стереометрії, щоб визначити взаєморозташування прямих у різних площинах та відстань між ними. У цьому випадку відрізок, що виконує функцію перпендикуляра, повинен мати прямий кут з обома прямими. Тоді числове значення даного відрізка показуватиме відстань між двома фігурами.