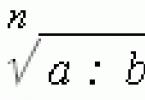
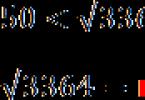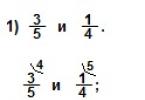Операції зі ступенями та корінням. Ступінь із негативним ,
нульовим та дробовим показником. Про висловлювання, які не мають сенсу.
Операції зі ступенями.
1. При множенні ступенів з однаковою основою їх показники складаються:
a m · a n = a m + n.
2. При розподілі ступенів з однаковою основою їх показники віднімаються .
3. Ступінь добутку двох або кількох співмножників дорівнює добутку ступенів цих співмножників.
(abc… ) n = a n· b n · c n…
4. Ступінь відношення (дробі) дорівнює відношенню ступенів ділимого (числителя) та дільника (знаменника):
(a/b ) n = a n / b n.
5. При зведенні ступеня до ступеня їх показники перемножуються:
(a m ) n = a m n .
Всі наведені вище формули читаються і виконуються в обох напрямках зліва направо і навпаки.
П р і м е р. (2 · 3 · 5 / 15) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .
Операції з корінням. У всіх наведених нижче формулах символ означає арифметичний корінь(підкорене вираз позитивно).
1. Корінь із твору кількох співмножників дорівнює твору коріння з цих співмножників:
2. Корінь із відношення дорівнює відношенню коріння ділимого та дільника:
![]()
3. При зведенні кореня до ступеня достатньо звести в цей ступінь підкорене число:

4. Якщо збільшити ступінь кореня в m раз і одночасно звести в m -у ступінь підкорене число, то значення кореня не зміниться:
![]()
5. Якщо зменшити ступінь кореня в m раз і одночасно витягти корінь m -ой ступеня з підкореного числа, то значення кореня незміниться:

Розширення поняття ступеня. Досі ми розглядали ступені лише з натуральним показником;але дії зі ступенями та корінням можуть призводити також до негативним, нульовимі дробовимпоказниками. Всі ці показники ступенів потребують додаткового визначення.
Ступінь із негативним показником. Ступінь деякого числа з негативним (цілим) показником визначається як одиниця, поділена на ступінь того ж числа з показником, що дорівнює абсолютній величинінегативного показника:

Тепер формула a m: a n= a m - n може бути використана не тільки приmбільше, ніж n, але і при mменшим, ніж n .
Примірник. a 4 :a 7 = a 4 - 7 = a - 3 .
Якщо ми хочемо, щоб формулаa m : a n= a m - nбула справедлива заm = n, нам потрібне визначення нульового ступеня.
Ступінь із нульовим показником. Ступінь будь-якого ненульового числа з нульовим показником дорівнює 1.
Приміри. 2 0 = 1, ( – 5) 0 = 1, (– 3 / 5) 0 = 1.
Ступінь із дробовим показником. Для того, щоб звести дійсне числоа в ступінь m/n , потрібно витягти корінь n – ступеня з m -ой ступеня цього числаа:

Про висловлювання, які не мають сенсу. Є кілька таких виразів.будь-яке число.
Справді, якщо припустити, що це вираз дорівнює деякому числу x, то згідно з визначенням операції поділу маємо: 0 = 0 · x. Але ця рівність має місце при будь-якому числі x, що і потрібно було довести.
Випадок 3.
0 0 - будь-яке число.
Справді,

Розв'язання. Розглянемо три основні випадки:
1) x = 0 – це значення не задовольняє даному рівнянню
(Чому?).
2) при x> 0 отримуємо: x/x = 1, тобто. 1 = 1, звідки слід,
що x- Будь-яке число; але беручи до уваги, що в
нашому випадку x> 0 , відповіддю єx > 0 ;
3) при x < 0 получаем: – x/x= 1, тобто . -1 = 1, отже,
І тут немає рішення.
Таким чином, x > 0.
Досить часто при вирішенні завдань ми стикаємося з великими числами, з яких треба витягти квадратний корінь. Багато учнів вирішують, що це помилка, і починають вирішувати весь приклад. У жодному разі не можна так чинити! На те є дві причини:
- Коріння з великих чисел справді зустрічається у завданнях. Особливо у текстових;
- Існує алгоритм, за допомогою якого це коріння вважається майже усно.
Цей алгоритм ми сьогодні розглянемо. Можливо, якісь речі здадуться вам незрозумілими. Але якщо ви уважно поставитеся до цього уроку, то отримаєте потужну зброю проти квадратного коріння.
Отже, алгоритм:
- Обмежити корінь, що шукається, зверху і знизу числами, кратними 10. Таким чином, ми скоротимо діапазон пошуку до 10 чисел;
- З цих 10 чисел відсіяти ті, які точно не можуть бути корінням. В результаті залишаться 1-2 числа;
- Звести ці 1-2 числа у квадрат. Те з них, квадрат якого дорівнює вихідному числу, і буде коренем.
Перш ніж застосовувати цей алгоритм працює на практиці, погляньмо на кожен окремий крок.
Обмеження коріння
Насамперед треба з'ясувати, між якими числами розташоване наше коріння. Дуже бажано, щоб числа були кратні десяти:
10 2 = 100;
20 2 = 400;
30 2 = 900;
40 2 = 1600;
...
90 2 = 8100;
100 2 = 10 000.
Отримаємо ряд чисел:
100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.
Що нам дають ці цифри? Все просто: ми маємо кордони. Візьмемо, наприклад, число 1296. Воно лежить між 900 і 1600. Отже, його корінь може бути менше 30 і більше 40:
[Підпис до малюнка]
Те саме — з будь-яким іншим числом, з якого можна знайти квадратний корінь. Наприклад, 3364:
[Підпис до малюнка]Таким чином, замість незрозумілого числа ми отримуємо цілком конкретний діапазон, де лежить вихідний корінь. Щоб ще більше звузити область пошуку, переходимо до другого кроку.
Відсів свідомо зайвих чисел
Отже, ми маємо 10 чисел — кандидатів на корінь. Ми отримали їх дуже швидко, без складних роздумів та множень у стовпчик. Час рухатися далі.
Не повірите, але зараз ми скоротимо кількість чисел-кандидатів до двох — і знову без складних обчислень! Достатньо знати спеціальне правило. Ось воно:
Остання цифра квадрата залежить лише від останньої цифри вихідного числа.
Інакше кажучи, досить поглянути на останню цифру квадрата — і ми одразу зрозуміємо, на що закінчується вихідне число.
Існує лише 10 цифр, які можуть стояти на останньому місці. Спробуємо з'ясувати, на що вони перетворюються при зведенні на квадрат. Погляньте на таблицю:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 1 | 4 | 9 | 6 | 5 | 6 | 9 | 4 | 1 | 0 |
Ця таблиця - ще один крок на шляху до обчислення кореня. Як бачите, цифри у другому рядку виявилися симетричними щодо п'ятірки. Наприклад:
2 2 = 4;
8 2 = 64 → 4.
Як бачите, остання цифра обох випадках однакова. А це означає, що, наприклад, корінь із 3364 обов'язково закінчується на 2 або на 8. З іншого боку, ми пам'ятаємо обмеження з попереднього пункту. Отримуємо:
 [Підпис до малюнка]
[Підпис до малюнка] Червоні квадрати показують, що ми поки що не знаємо цієї цифри. Але корінь лежить у межах від 50 до 60, на якому є тільки два числа, що закінчуються на 2 і 8:
[Підпис до малюнка]От і все! З усіх можливих коренів ми залишили лише два варіанти! І це у найважчому випадку, адже остання цифра може бути 5 чи 0. І тоді залишиться єдиний кандидат у корені!
Фінальні обчислення
Отже, у нас залишилося 2 числа-кандидати. Як дізнатися, яке з них є коренем? Відповідь очевидна: звести обидва числа у квадрат. Те, що у квадраті дасть вихідне число, і буде коренем.
Наприклад, для числа 3364 ми знайшли два числа-кандидати: 52 та 58. Зведемо їх у квадрат:
52 2 = (50 +2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;
58 2 = (60 − 2) 2 = 3600 − 2 · 60 · 2 + 4 = 3364.
От і все! Вийшло, що корінь дорівнює 58! При цьому, щоб спростити обчислення, я скористався формулою квадратів суми та різниці. Завдяки чому навіть не довелося множити числа у стовпчик! Це ще один рівень оптимізації обчислень, але, зрозуміло, не обов'язковий:)
Приклади обчислення коренів
Теорія – це, звичайно, добре. Але перевіримо її на практиці.
[Підпис до малюнка]
Для початку з'ясуємо, між якими числами лежить число 576:
400 < 576 < 900
20 2 < 576 < 30 2
Тепер дивимось на останню цифру. Вона дорівнює 6. Коли це відбувається? Тільки якщо корінь закінчується на 4 або 6. Отримуємо два числа:
Залишилося звести кожне число квадрат і порівняти з вихідним:
24 2 = (20 + 4) 2 = 576
Чудово! Перший квадрат виявився дорівнює вихідному числу. Значить, це є корінь.
Завдання. Обчисліть квадратний корінь:
[Підпис до малюнка]
900 < 1369 < 1600;
30 2 < 1369 < 40 2;
Дивимося на останню цифру:
1369 → 9;
33; 37.
Зводимо у квадрат:
33 2 = (30 + 3) 2 = 900 + 2 · 30 · 3 + 9 = 1089 ≠ 1369;
37 2 = (40 − 3) 2 = 1600 − 2 · 40 · 3 + 9 = 1369.
Ось і відповідь: 37.
Завдання. Обчисліть квадратний корінь:
[Підпис до малюнка]
Обмежуємо число:
2500 < 2704 < 3600;
50 2 < 2704 < 60 2;
Дивимося на останню цифру:
2704 → 4;
52; 58.
Зводимо у квадрат:
52 2 = (50 + 2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;
Отримали відповідь: 52. Друге число зводити до квадрата вже не потрібно.
Завдання. Обчисліть квадратний корінь:
[Підпис до малюнка]
Обмежуємо число:
3600 < 4225 < 4900;
60 2 < 4225 < 70 2;
Дивимося на останню цифру:
4225 → 5;
65.
Як бачимо, після другого кроку залишився лише один варіант: 65. Це і шуканий корінь. Але давайте таки зведемо його в квадрат і перевіримо:
65 2 = (60 + 5) 2 = 3600 + 2 · 60 · 5 + 25 = 4225;
Все правильно. Записуємо відповідь.
Висновок
На жаль, не краще. Давайте розберемося у причинах. Їх дві:
- На будь-якому нормальному іспиті з математики, чи то ГІА чи ЄДІ, користуватися калькуляторами заборонено. І за пронесений до класу калькулятор можуть запросто вигнати з іспиту.
- Не уподібнюйтесь тупим американцям. Які не те що коріння - вони два простих числа скласти не можуть. А побачивши дробів вони взагалі починається істерика.
Наявність квадратних коренів у вираженні ускладнює процес розподілу, проте існують правила, за допомогою яких робота з дробами стає значно простішою.
Єдине, що необхідно весь час пам'ятати- підкорені вирази поділяються на підкорені вирази, а множники на множники. У процесі поділу квадратного коріння ми спрощуємо дріб. Також, нагадаємо, що корінь може перебувати у знаменнику.
Метод 1. Розподіл підкорених виразів
Алгоритм дій:
Записати дріб
Якщо вираз не представлений у вигляді дробу, необхідно його так записати, тому так легше дотримуватися принципу поділу квадратного коріння.
Приклад 1
144 ÷ 36 , цей вираз слід переписати так: 144 36
Використовувати один знак кореня
Якщо і в чисельнику, і знаменнику є квадратне коріння, необхідно записати їх підкорені вирази під одним знаком кореня, щоб зробити процес розв'язання простіше.
Нагадуємо, що підкореним виразом (чи числом) є виразом під знаком кореня.
Приклад 2
144 36 . Цей вираз слід записати так: 144 36
Розділити підкорені вирази
Просто розділіть один вираз на інший, а результат запишіть під знаком кореня.
Приклад 3
144 36 = 4 , запишемо цей вираз так: 144 36 = 4
Спростити підкорене вираз (якщо необхідно)
Якщо підкорене вираз або один із множників є повним квадратом, спрощуйте такий вираз.
Нагадаємо, що повним квадратом є число, яке є квадратом деякого цілого числа.
Приклад 4
4 - Повний квадрат, тому що 2 × 2 = 4 . З цього випливає:
4 = 2 × 2 = 2. Тому 14436 = 4 = 2 .
Метод 2. Розкладання підкореного виразу на множники
Алгоритм дій:
Записати дріб
Перепишіть вираз у вигляді дробу (якщо воно представлено так). Це значно полегшує процес поділу виразів із квадратним корінням, особливо при розкладанні на множники.
Приклад 5
8 ÷ 36 , переписуємо так 8 36
Розкласти на множники кожен із підкорених виразів
Число під коренем розкладіть на множники, як і будь-яке інше ціле число, тільки запишіть множники під знаком кореня.
Приклад 6
8 36 = 2 × 2 × 2 6 × 6
Спростити чисельник та знаменник дробу
Для цього слід винести з-під знака кореня множники, що є повними квадратами. Таким чином, множник підкореного виразу стане множником перед знаком кореня.
Приклад 7
2 2 6 6 × 6 2 × 2 × 2 , з цього випливає: 8 36 = 2 2 6
Раціоналізувати знаменник (позбутися кореня)
У математиці існують правила, якими залишати корінь у знаменнику - ознака поганого тону, тобто. не можна. Якщо в знаменнику є квадратний корінь, то позбавляйтеся його.
Помножте чисельник і знаменник на квадратний корінь, якого необхідно позбутися.
Приклад 8
У виразі 6 2 3 необхідно помножити чисельник і знаменник на 3 щоб позбутися його в знаменнику:
6 2 3 × 3 3 = 6 2 × 3 3 × 3 = 6 6 9 = 6 6 3
Спростити отриманий вираз (якщо необхідно)
Якщо в чисельнику та знаменнику є числа, які можна і потрібно скоротити. Спрощуйте такі вирази, як будь-який дріб.
Приклад 9
2 6 спрощується до 1 3; таким чином 2 2 6 спрощується до 1 2 3 = 2 3
Метод 3. Розподіл квадратних коренів з множниками
Алгоритм дій:
Спростити множники
Нагадаємо, що множники є числа, що стоять перед знаком кореня. Для спрощення множників потрібно розділити або скоротити їх. Підкорені вирази не чіпайте!
Приклад 10
4 32 6 16 . Спочатку скорочуємо 46: ділимо на 2 і чисельник, і знаменник: 46 = 23.
Спростити квадратне коріння
Якщо чисельник повністю ділиться на знаменник, то діліть. Якщо ні, то спрощуйте підкорені вирази, як будь-які інші.
Приклад 11
32 ділиться націло на 16 тому: 32 16 = 2
Помножити спрощені множники на спрощене коріння
Пам'ятаємо про правило: не залишати у знаменнику коріння. Тому просто перемножуємо чисельник і знаменник цього коріння.
Приклад 12
2 3 × 2 = 2 2 3
Раціоналізувати знаменник (позбутися кореня в знаменнику)
Приклад 13
4 3 2 7 . Слід помножити чисельник і знаменник на 7 щоб позбавитися від кореня в знаменнику.
4 3 7 × 7 7 = 4 3 × 7 7 × 7 = 4 21 49 = 4 21 7
Метод 4. Розподіл на двочлен із квадратним коренем
Алгоритм дій:
Визначити, чи двочлен (біном) у знаменнику
Нагадаємо, що двочлен є виразом, який включає 2 одночлени. Такий метод має місце лише у випадках, коли в знаменнику двочлен з квадратним коренем.
Приклад 14
1 5 + 2 - у знаменнику присутній біном, оскільки є два одночлени.
Знайти вираз, пов'язаний біном
Нагадаємо, що сполучений біном є двочленом з тими самими одночленами, але з протилежними знаками. Щоб спростити вираз і позбавитися кореня в знаменнику, слід перемножити сполучені біноми.
Приклад 15
5 + 2 і 5 - 2 - сполучені біноми.
Помножити чисельник та знаменник на двочлен, який пов'язаний біном у знаменнику
Така опція допоможе позбавитися кореня в знаменнику, оскільки добуток сполучених двочленів дорівнює різниці квадратів кожного члена біномів: (a - b) (a + b) = a 2 - b 2
Приклад 16
1 5 + 2 = 1 (5 - 2) (5 - 2) (5 + 2) = 5 - 2 (5 2 - (2) 2 = 5 - 2 25 - 2 = 5 - 2 23 .
З цього випливає: 15 + 2 = 5 - 223.
Поради:
- Якщо ви працюєте з квадратним корінням змішаних чисел, то перетворюйте їх на неправильний дріб.
- Відмінність додавання і віднімання від поділу - підкорені вирази у разі поділу не рекомендується спрощувати (за рахунок повних квадратів).
- Ніколи (!) не залишайте коріння у знаменнику.
- Жодних десяткових дробів або змішаних перед коренем - необхідно перетворити їх на звичайний дріб, а потім спростити.
- У знаменнику сума чи різниця двох одночленів? Помножте такий біном на пов'язаний йому двочлен і позбавтеся кореня в знаменнику.
Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter
Щоб успішно використовувати практично операцію вилучення кореня, потрібно познайомитися з властивостями цієї операції.
Усі властивості формулюються і доводяться лише для невід'ємних значень змінних, які під знаками коренів.
Теорема 1. Корінь n-го ступеня (n=2, 3, 4,...) з добутку двох невід'ємних чіпсел дорівнює добутку коріння n-го ступеня з цих чисел:
Примітка:
1.
Теорема 1 залишається справедливою і для випадку, коли підкорене вираз є твір більш ніж двох невід'ємних чисел.
Теорема 2.Якщо,
і n - натуральне число, більше 1, то справедлива рівність
Коротка(хоча й неточне) формулювання, яке зручніше використовувати на практиці: корінь із дробу дорівнює дробу від коріння.
Теорема 1 дозволяє нам перемножувати т тільки коріння однакового ступеня
, тобто. лише коріння з однаковим показником.
Теорема 3.Якщо ,k - натуральне число і n - натуральне число, більше 1, то справедлива рівність
Іншими словами, щоб звести корінь у натуральний ступінь, достатньо звести в цей ступінь підкорене вираз.
Це - наслідок теореми 1. Справді, наприклад, для к = 3 отримуємо: Так само можна міркувати у разі будь-якого іншого натурального значення показника до.
Теорема 4.Якщо ,k, n - натуральні числа, більші за 1, то справедлива рівність
Іншими словами, щоб витягти корінь з кореня, достатньо перемножити показники коріння.
Наприклад,
Будьте уважні!Ми дізналися, що над корінням можна здійснювати чотири операції: множення, розподіл, зведення в ступінь та вилучення кореня (з кореня). А як же справа зі складанням і відніманням коренів? Ніяк.
Наприклад, замість не можна написати Справді, Але ж очевидно, що
Теорема 5. Якщо показники кореня і підкореного виразу помножити чи розділити одне і те натуральне число, то значення кореня зміниться, тобто.
Приклади вирішення завдань
приклад 1.Обчислити
Рішення.Скориставшись першою властивістю коріння (теорема 1), отримаємо:
приклад 2.Обчислити
Рішення.Обернемо змішане число в неправильний дріб.
Маємо Скориставшись другою властивістю коренів ( теорема 2
), отримаємо:
![]()
приклад 3.Обчислити: ![]()
Рішення.Будь-яка формула в алгебрі, як вам добре відомо, використовується не лише «зліва направо», а й «справа наліво». Так, перша властивість коренів означає, що можна уявити у вигляді і, навпаки, можна замінити виразом . Те саме стосується і другої властивості коренів. Враховуючи це, виконаємо обчислення.
Вітаю: сьогодні ми розбиратимемо коріння — одну з найбільш мозкових тем 8-го класу.:)
Багато хто плутається в корінні не тому, що воно складне (чого там складного — пара визначень і ще пара властивостей), а тому що в більшості шкільних підручників коріння визначається через такі нетрі, що розібратися в цій писанині можуть хіба самі автори підручників. Та й то лише з пляшкою гарного віскі.
Тому зараз я дам найправильніше і найписьменніше визначення кореня - єдине, яке вам справді слід запам'ятати. А вже потім поясню: навіщо все це потрібно і як застосовувати на практиці.
Але спочатку запам'ятайте один важливий момент, про який багато укладачів підручників чомусь «забувають»:
Коріння буває парного ступеня (наш улюблений $\sqrt(a)$, а також всякі $\sqrt(a)$ і навіть $\sqrt(a)$) і непарного ступеня (всякі $\sqrt(a)$, $\ sqrt(a)$ і т.д.). І визначення кореня непарного ступеня дещо відрізняється від парного.
Ось у цьому гребінці «дещо відрізняється» приховано, напевно, 95% всіх помилок і непорозуміння, пов'язаного з корінням. Тому давайте раз і назавжди розберемося з термінологією:
Визначення. Корінь парного ступеня nз $a$ - це будь-яке невід'ємнечисло $b$ таке, що $((b)^(n))=a$. А корінь непарного ступеня з того ж числа $a$ - це взагалі будь-яке число $b$, для якого виконується та ж рівність: $((b)^(n))=a$.
У будь-якому випадку корінь позначається так:
\(a)\]
Число $n$ у такому записі називається показником кореня, а число $a$ - підкореним виразом. Зокрема, при $n=2$ отримаємо наш «улюблений» квадратний корінь (до речі, це корінь парного ступеня), а за $n=3$ — кубічний (ступінь непарний), який теж часто зустрічається в завданнях та рівняннях.
приклади. Класичні приклади квадратного коріння:
\[\begin(align) & \sqrt(4)=2; \ \ & \ sqrt (81) = 9; \ & \ sqrt (256) = 16. \\ \end(align)\]
До речі, $ sqrt (0) = 0 $, а $ sqrt (1) = 1 $. Це цілком логічно, оскільки $((0)^(2))=0$ і $((1)^(2))=1$.
Кубічні коріння теж часто зустрічаються — не треба їх боятися:
\[\begin(align) & \sqrt(27)=3; \\ \sqrt(-64)=-4; \ \ \ \ sqrt (343) = 7. \\ \end(align)\]
Ну, і парочка «екзотичних прикладів»:
\[\begin(align) & \sqrt(81)=3; \\ & \sqrt(-32)=-2. \\ \end(align)\]
Якщо ви не зрозуміли, у чому різниця між парним та непарним ступенем — перечитайте визначення ще раз. Це дуже важливо!
А ми тим часом розглянемо одну неприємну особливість коренів, через яку нам потрібно було вводити роздільне визначення для парних і непарних показників.
Навіщо взагалі потрібне коріння?
Прочитавши визначення, багато учнів запитають: Що курили математики, коли це вигадували? І справді: навіщо взагалі потрібне все це коріння?
Щоб відповісти на це питання, повернемося на хвилинку до початкових класів. Згадайте: у ті далекі часи, коли дерева були зеленішими, а пельмені смачнішими, основна наша турбота була в тому, щоб правильно множити числа. Ну, щось у дусі «п'ять на п'ять-двадцять п'ять», ось це все. Але можна множити числа не парами, а трійками, четвірками і взагалі цілими комплектами:
\[\begin(align) & 5\cdot 5=25; \ & 5 \ cdot 5 \ cdot 5 = 125; \ & 5 \ cdot 5 \ cdot 5 \ cdot 5 = 625; \ \ 5 \ cdot 5 \ cdot 5 \ cdot 5 \ cdot 5 = 3125; \\ 5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5=15\ 625. \end(align)\]
Однак суть не в цьому. Фішка в іншому: математики - люди ліниві, тому їм було в лом записувати множення десяти п'ятірок ось так:
Тому вони вигадали ступеня. Чому б замість довгого рядка не записати кількість множників у вигляді верхнього індексу? Типу такого:
Це дуже зручно! Всі обчислення скорочуються в рази, і можна не витрачати купу аркушів пергаменту блокнотиків на запис якогось 5 183 . Такий запис назвали ступенем числа, у нього знайшли купу властивостей, але щастя виявилося недовгим.
Після грандіозної п'янки, яку організували саме з приводу «відкриття» ступенів, якийсь особливо затятий математик раптом запитав: «А що, якщо нам відомий ступінь числа, але невідомо саме число?» Ось, дійсно, якщо нам відомо, що деяке число $b$, припустимо, в 5-му ступені дає 243, то як нам здогадатися, чому одно число $b$?
Проблема ця виявилася набагато глобальнішою, ніж може здатися на перший погляд. Тому що з'ясувалося, що для більшості готових ступенів таких вихідних чисел немає. Судіть самі:
\[\begin(align) & ((b)^(3))=27Rightarrow b=3cdot 3cdot 3Rightarrow b=3; \ & ((b) ^ (3)) = 64 Rightarrow b = 4 cdot 4 cdot 4 Rightarrow b = 4. \\ \end(align)\]
А що якщо $((b)^(3))=50$? Виходить, що потрібно знайти якесь число, яке тричі помножене саме на себе дасть нам 50. Але що це за число? Воно явно більше 3, оскільки 3 3 = 27< 50. С тем же успехом оно меньше 4, поскольку 4 3 = 64 >50. Тобто. це число лежить десь між трійкою і четвіркою, але чому воно одно - фіг зрозумієш.
Саме для цього математики і придумали коріння $n$-го ступеня. Саме для цього ввели піктограму радикала $\sqrt(*)$. Щоб позначити те саме число $b$, яке в даній мірі дасть нам заздалегідь відому величину
\[\sqrt[n](a)=b\Rightarrow ((b)^(n))=a\]
Не сперечаюся: найчастіше це коріння легко вважається — ми бачили кілька таких прикладів вище. Але все-таки в більшості випадків, якщо ви загадаєте довільне число, а потім спробуєте витягти з нього корінь довільного ступеня, на вас чекає жорстокий облом.
Та що там! Навіть найпростіший і всім знайомий $\sqrt(2)$ не можна уявити у звичному нам вигляді - як ціле число або дрібничка. А якщо ви вб'єте це число в калькулятор, то побачите це:
\[\sqrt(2)=1,414213562...\]
Як бачите, після коми йде нескінченна послідовність цифр, які не підкоряються жодній логіці. Можна, звичайно, округлити це число, щоб швидко порівняти з іншими числами. Наприклад:
\[\sqrt(2)=1,4142...\approx 1,4 \lt 1,5\]
Або ось ще приклад:
\[\sqrt(3)=1,73205...\approx 1,7 \gt 1,5\]
Але ці округлення, по-перше, досить грубі; а по-друге, працювати з приблизними значеннями теж треба вміти, інакше можна зловити купу неочевидних помилок (до речі, навик порівняння та округлення обов'язково перевіряють на профільному ЄДІ).
Тому в серйозній математиці без коріння не обійтися - вони є такими ж рівноправними представниками багатьох дійсних чисел $\mathbb(R)$, як і давно знайомі нам дроби і цілі числа.
Неможливість уявити корінь як дробу виду $\frac(p)(q)$ означає, що це корінь перестав бути раціональним числом. Такі числа називаються ірраціональними, і їх не можна точно уявити інакше як за допомогою радикала або інших спеціально призначених для цього конструкцій (логарифмів, ступенів, меж тощо). Але про це — іншого разу.
Розглянемо кілька прикладів, де після всіх обчислень ірраціональні числа все ж таки залишаться у відповіді.
\[\begin(align) & \sqrt(2+\sqrt(27))=\sqrt(2+3)=\sqrt(5)\approx 2,236... \\ & \sqrt(\sqrt(-32) ))=\sqrt(-2)\approx -1,2599... \\ \end(align)\]
Природно, на вигляд кореня практично неможливо здогадатися про те, які числа будуть йти після коми. Втім, можна порахувати на калькуляторі, але навіть найдосконаліший калькулятор дат нам лише кілька перших цифр ірраціонального числа. Тому набагато правильніше записати відповіді у вигляді $sqrt(5)$ і $sqrt(-2)$.
Саме для цього їх і вигадали. Щоб зручно записувати відповіді.
Чому потрібні два визначення?
Уважний читач уже напевно помітив, що всі квадратні корені, наведені в прикладах, витягуються з позитивних чисел. Ну, принаймні з нуля. А ось кубічні корені незворушно витягуються абсолютно з будь-якого числа — хоч позитивного, хоч негативного.
Чому так відбувається? Подивіться графік функції $y=((x)^(2))$:
 Графік квадратичної функції дає два корені: позитивний та негативний
Графік квадратичної функції дає два корені: позитивний та негативний Спробуємо за допомогою цього графіка порахувати $sqrt (4) $. Для цього на графіку проведено горизонтальну лінію $y=4$ (позначено червоним кольором), яка перетинається з параболою у двох точках:$((x)_(1))=2$ і $((x)_(2)) =-2 $. Це цілком логічно, оскільки
З першим числом все зрозуміло — воно позитивне, тому воно є корінь:
Але що робити тоді з другою точкою? Типу у четвірки відразу два корені? Адже якщо звести до квадрата число −2, ми теж отримаємо 4. Чому б тоді не записати $\sqrt(4)=-2$? І чому вчителі дивляться на такі записи так, ніби хочуть вас зжерти?:)
У тому й біда, що якщо не накладати жодних додаткових умов, то квадратного коріння у четвірки буде два — позитивне і негативне. І в будь-якого позитивного числа їх також буде два. А ось у негативних чисел коріння взагалі не буде — це видно все за тим же графіком, оскільки парабола ніде не опускається нижче за осю y, тобто. не набуває негативних значень.
Подібна проблема виникає у всіх коренів з парним показником:
- Строго кажучи, коріння з парним показником $n$ у кожного позитивного числа буде відразу дві штуки;
- З негативних чисел корінь із парним $n$ взагалі не витягується.
Саме тому у визначенні кореня парного ступеня $n$ спеціально обговорюється, що відповідь має бути невід'ємною кількістю. Так ми позбавляємося неоднозначності.
Зате для непарних $n$ такої проблеми немає. Щоб переконатися в цьому, погляньмо на графік функції $y=((x)^(3))$:
 Кубічна парабола набуває будь-яких значень, тому кубічний корінь витягується з будь-якого числа.
Кубічна парабола набуває будь-яких значень, тому кубічний корінь витягується з будь-якого числа. З цього графіка можна зробити два висновки:
- Гілки кубічної параболи, на відміну від звичайної, йдуть на нескінченність в обидві сторони - і вгору, і вниз. Тому на якій би висоті ми не проводили горизонтальну пряму, ця пряма обов'язково перетнеться з нашим графіком. Отже, кубічний корінь можна отримати завжди, абсолютно з будь-якого числа;
- Крім того, таке перетин завжди буде єдиним, тому не потрібно думати, яке число вважати «правильним» коренем, а на яке забити. Саме тому визначення коренів для непарного ступеня простіше, ніж для парної (відсутня вимога невід'ємності).
Жаль, що ці прості речі не пояснюють у більшості підручників. Натомість нам починають ширяти мозок усілякими арифметичними корінням та їх властивостями.
Так, я не сперечаюся: що таке арифметичний корінь теж треба знати. І я докладно розповім про це в окремому уроці. Сьогодні ми теж поговоримо про нього, оскільки без нього всі роздуми про коріння $n$-ї кратності були б неповними.
Але спочатку треба чітко засвоїти те визначення, яке я дав вище. Інакше через велику кількість термінів у голові почнеться така каша, що в результаті взагалі нічого не зрозумієте.
А всього й треба зрозуміти різницю між парними та непарними показниками. Тому ще раз зберемо все, що дійсно потрібно знати про коріння:
- Корінь парного ступеня існує лише з невід'ємного числа і сам є невід'ємним числом. Для негативних чисел такий корінь невизначений.
- А ось корінь непарного ступеня існує з будь-якого числа і може бути будь-яким числом: для позитивних чисел він позитивний, а для негативних — як натякає кеп, негативний.
Хіба це складно? Ні, не складно. Зрозуміло? Та взагалі очевидно! Тому зараз ми трохи потренуємось із обчисленнями.
Основні властивості та обмеження
Коріння має багато дивних властивостей і обмежень — про це буде окремий урок. Тому зараз ми розглянемо лише найважливішу «фішку», яка стосується лише коріння з парним показником. Запишемо цю властивість у вигляді формули:
\[\sqrt(((x)^(2n)))=\left| x \right|\]
Іншими словами, якщо звести число в парний ступінь, а потім з цього витягти корінь того ж ступеня, ми отримаємо не вихідне число, яке модуль . Це проста теорема, яка легко доводиться (досить окремо розглянути невід'ємні $x$, а потім окремо негативні). Про неї постійно товкмачать вчителі, її дають у кожному шкільному підручнику. Але як тільки справа доходить до вирішення ірраціональних рівнянь (тобто рівнянь, що містять знак радикала), учні дружно забувають цю формулу.
Щоб детально розібратися в питанні, давайте на хвилину забудемо всі формули і спробуємо порахувати два числа напролом:
\[\sqrt(((3)^(4)))=?\quad \sqrt(((\left(-3 \right))^(4)))=?\]
Це дуже звичайні приклади. Перший приклад вирішить більшість людей, а ось на другому багато хто залипає. Щоб без проблем вирішити будь-яку подібну хрень, завжди враховуйте порядок дій:
- Спочатку число зводиться у четвертий ступінь. Ну, це нескладно. Вийде нове число, яке навіть у таблиці множення можна знайти;
- І ось уже з цього нового числа необхідно витягти корінь четвертого ступеня. Тобто. ніякого «скорочення» коріння та ступенів не відбувається — це послідовні дії.
Розберемося з першим виразом: $ \ sqrt (((3) ^ (4))) $. Очевидно, що спочатку треба порахувати вираз, що стоїть під коренем:
\[((3)^(4))=3\cdot 3\cdot 3\cdot 3=81\]
Потім витягаємо корінь четвертого ступеня з числа 81:
Тепер зробимо те саме з другим виразом. Спочатку зводимо число −3 у четверту міру, навіщо потрібно помножити його саме він 4 разу:
\[((\left(-3 \right))^(4))=\left(-3 \right)\cdot \left(-3 \right)\cdot \left(-3 \right)\cdot \ left(-3 \right)=81\]
Отримали позитивне число, оскільки загальна кількість мінусів у творі — 4 штуки, і всі вони взаємно знищиться (адже мінус на мінус дає плюс). Далі знову витягаємо корінь:
У принципі, цей рядок можна було не писати, оскільки і їжу зрозуміло, що відповідь вийде одна й та сама. Тобто. парний корінь з тієї ж парної міри «спалює» мінуси, і в цьому сенсі результат не відрізняється від звичайного модуля:
\[\begin(align) & \sqrt(((3)^(4)))=\left| 3 \right|=3; \\ & \sqrt(((\left(-3 \right))^(4)))=\left| -3 \right|=3. \\ \end(align)\]
Ці обчислення добре узгоджуються з визначенням кореня парного ступеня: результат завжди негативний, та й під знаком радикала теж завжди стоїть невід'ємне число. В іншому випадку корінь не визначений.
Зауваження щодо порядку дій
- Запис $\sqrt(((a)^(2)))$ означає, що ми спочатку зводимо число $a$ у квадрат, а потім витягуємо з отриманого значення квадратний корінь. Отже, ми можемо бути впевнені, що під знаком кореня завжди сидить невід'ємне число, оскільки $((a)^(2))\ge 0$ у будь-якому випадку;
- А ось запис $((\left(\sqrt(a) \right))^(2))$, навпаки, означає, що ми спочатку витягаємо корінь з деякого числа $a$ і лише потім зводимо результат у квадрат. Тому число $a$ в жодному разі не може бути негативним - це обов'язкова вимога, закладена у визначення.
Таким чином, у жодному разі не можна бездумно скорочувати коріння та ступеня, тим самим нібито «спрощуючи» вихідний вираз. Тому що якщо під коренем стоїть негативне число, а його показник є парним, ми отримаємо купу проблем.
Втім, всі ці проблеми є актуальними лише для парних показників.
Винесення мінуса з-під знака кореня
Природно, коріння з непарними показниками теж має свою фішку, якої в принципі не буває у парних. А саме:
\[\sqrt(-a)=-\sqrt(a)\]
Коротше кажучи, можна виносити мінус з-під знаку коріння непарного ступеня. Це дуже корисна властивість, яка дозволяє «викинути» всі мінуси назовні:
\[\begin(align) & \sqrt(-8)=-\sqrt(8)=-2; \\ & \sqrt(-27)\cdot \sqrt(-32)=-\sqrt(27)\cdot \left(-\sqrt(32) \right)= \\ & =\sqrt(27)\cdot \ sqrt (32) = \ \ & = 3 \ cdot 2 = 6. \end(align)\]
Ця проста властивість значно спрощує багато обчислень. Тепер не треба переживати: раптом під коренем затесався негативний вираз, а ступінь у кореня виявився парним? Достатньо лише «викинути» всі мінуси за межі коріння, після чого їх можна буде множити один на одного, ділити і взагалі робити багато підозрілих речей, які у випадку з «класичним» корінням гарантовано приведуть нас до помилки.
І ось тут на сцену виходить ще одне визначення — те саме, з якого в більшості шкіл починають вивчення ірраціональних виразів. І без якого наші міркування були б неповними. Зустрічайте!
Арифметичний корінь
Давайте припустимо на хвилинку, що під знаком кореня можуть бути лише позитивні числа або в крайньому випадку нуль. Заб'ємо на парні/непарні показники, заб'ємо на всі визначення, наведені вище - працюватимемо тільки з невід'ємними числами. Що тоді?
А тоді ми отримаємо арифметичний корінь — він частково перетинається з нашими «стандартними» визначеннями, але все ж таки відрізняється від них.
Визначення. Арифметичним коренем $n$-го ступеня з невід'ємного числа $a$ називається таке невід'ємне число $b$, що $((b)^(n))=a$.
Як бачимо, нас більше не цікавить парність. Натомість її з'явилося нове обмеження: підкорене вираз тепер завжди невід'ємно, та й сам корінь теж негативний.
Щоб краще зрозуміти, чим арифметичний корінь відрізняється від звичайного, погляньте на вже знайомі нам графіки квадратної та кубічної параболи:
 Область пошуку арифметичного кореня – невід'ємні числа
Область пошуку арифметичного кореня – невід'ємні числа Як бачите, відтепер нас цікавлять ті шматки графіків, які розташовані в першій координатній чверті — там, де координати $x$ і $y$ позитивні (або хоча б нуль). Більше не потрібно дивитися на показник, щоб зрозуміти: чи маємо ми право ставити під корінь негативне число чи ні. Тому що негативні числа більше, у принципі, не розглядаються.
Можливо, ви запитаєте: "Ну і навіщо нам таке кастроване визначення?" Або: «Чому не можна обійтися стандартним визначенням, даним вище?»
Що ж, наведу лише одну властивість, через яку нове визначення стає доцільним. Наприклад, правило зведення в ступінь:
\[\sqrt[n](a)=\sqrt(((a)^(k)))\]
Зверніть увагу: ми можемо звести підкорене вираз у будь-який ступінь і одночасно помножити на цей самий ступінь показник кореня — і в результаті вийде те саме число! Ось приклади:
\[\begin(align) & \sqrt(5)=\sqrt(((5)^(2)))=\sqrt(25) \\ & \sqrt(2)=\sqrt(((2)^ (4)))=\sqrt(16) \\ \end(align)\]
Ну, і що в цьому такого? Чому ми не могли це зробити раніше? А ось чому. Розглянемо простий вираз: $\sqrt(-2)$ — це цілком нормальне у нашому класичному розумінні, але абсолютно неприпустимо з погляду арифметичного кореня. Спробуємо перетворити його:
$\begin(align) & \sqrt(-2)=-\sqrt(2)=-\sqrt(((2)^(2)))=-\sqrt(4) \lt 0; \\ & \sqrt(-2)=\sqrt(((\left(-2 \right))^(2)))=\sqrt(4) \gt 0. \\ \end(align)$
Як бачите, у першому випадку ми винесли мінус з-під радикала (маємо повне право, тому що показник непарний), а в другому — скористалися зазначеною формулою. Тобто. з погляду математики все зроблено за правилами.
WTF?! Як одне й те число може бути і позитивним, і негативним? Ніяк. Просто формула зведення в ступінь, який чудово працює для позитивних чисел і нуля, починає видавати повну брехню у випадку з негативними числами.
Ось для того, щоб позбутися подібної неоднозначності, і вигадали арифметичні коріння. Їм присвячений окремий великий урок, де ми докладно розглядаємо всі властивості. Отже зараз не будемо на них зупинятися — урок і так вийшов занадто затягнутим.
Алгебраїчне коріння: для тих, хто хоче знати більше
Довго думав: виносити цю тему до окремого параграфу чи ні. Зрештою вирішив залишити тут. Цей матеріал призначений для тих, хто хоче зрозуміти коріння ще краще – вже не на середньому «шкільному» рівні, а на наближеному до олімпіадного.
Так ось: крім «класичного» визначення кореня $n$-го ступеня з числа та пов'язаного з ним поділу на парні та непарні показники є більш «доросле» визначення, яке взагалі не залежить від парності та інших тонкощів. Це називається алгебраїчним коренем.
Визначення. Алгебраїчний корінь $n$-го ступеня з-поміж будь-якого $a$ — це безліч всіх чисел $b$ таких, що $((b)^(n))=a$. Для такого коріння немає усталеного позначення, тому просто поставимо рису зверху:
\[\overline(\sqrt[n](a))=\left\( b\left| b\in \mathbb(R);((b)^(n))=a \right. \right\) \]
Принципова відмінність від стандартного визначення, наведеного на початку уроку, полягає в тому, що корінь алгебри — це не конкретне число, а безліч. Оскільки ми працюємо з дійсними числами, це безліч буває лише трьох типів:
- Порожня безліч. Виникає у разі, коли потрібно знайти алгебраїчний корінь парного ступеня негативного числа;
- Безліч, що складається з одного-єдиного елемента. Усі коріння непарних ступенів, а також корені парних ступенів з нуля потрапляють до цієї категорії;
- Нарешті, безліч може включати два числа - ті самі $((x)_(1))$ і $((x)_(2))=-((x)_(1))$, яке ми бачили на графіку квадратичні функції. Відповідно, такий розклад можливий лише за вилучення кореня парного ступеня з позитивного числа.
Останній випадок заслуговує на докладніший розгляд. Порахуємо кілька прикладів, щоб зрозуміти різницю.
приклад. Обчисліть вирази:
\[\overline(\sqrt(4));\quad \overline(\sqrt(-27));\quad \overline(\sqrt(-16)).\]
Рішення. З першим виразом все просто:
\[\overline(\sqrt(4))=\left\( 2;-2 \right\)\]
Саме два числа входять до складу множини. Тому що кожен із них у квадраті дає четвірку.
\[\overline(\sqrt(-27))=\left\( -3 \right\)\]
Тут бачимо безліч, що складається лише з одного числа. Це цілком логічно, оскільки показник кореня непарний.
Нарешті, останній вираз:
\[\overline(\sqrt(-16))=\varnothing \]
Отримали порожню множину. Тому що немає жодного дійсного числа, яке при зведенні в четвертий (тобто парний!) ступінь дасть нам негативне число −16.
Фінальне зауваження. Зверніть увагу: я не випадково скрізь зазначав, що ми працюємо з дійсними числами. Тому що є ще комплексні числа — там цілком можна порахувати і $sqrt(-16)$, і багато інших дивних речей.
Однак у сучасному шкільному курсі математики комплексні числа майже зустрічаються. Їх викреслили з більшості підручників, оскільки наші чиновники вважають цю тему «надто складною для розуміння».
На цьому все. У наступному уроці ми розглянемо всі ключові властивості коренів і навчимося, нарешті, спрощувати ірраціональні вирази.