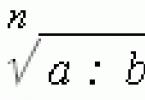
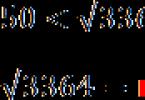Operácie s mocnosťami a koreňmi. Stupeň s negatívom ,

nulové a zlomkové indikátor. O výrazoch, ktoré nedávajú zmysel.

Operácie so stupňami.

1. Pri násobení mocnín s rovnakým základom sa ich ukazovatele sčítajú:

a m · a n = a m + n.

2. Pri delení stupňov s rovnakým základom ich ukazovatele odpočítané .

3. Stupeň súčinu dvoch alebo viacerých faktorov sa rovná súčinu stupňov týchto faktorov.

(abc… ) n = a n· b n · c n…

4. Stupeň pomeru (zlomok) sa rovná pomeru stupňov dividendy (čitateľ) a deliteľa (menovateľ):

(a/b ) n = a n / b n.

5. Pri zvýšení stupňa na mocninu sa ich ukazovatele násobia:

(a m ) n = a m n.

Všetky vyššie uvedené vzorce sa čítajú a vykonávajú v oboch smeroch zľava doprava a naopak.

PRÍKLAD (2 · 3 · 5/15)² = 2² 3² 5² / 15² = 900 / 225 = 4 .

Operácie s koreňmi. Vo všetkých nižšie uvedených vzorcoch symbol znamená aritmetický koreň(radikálny výraz je pozitívny).

1. Koreň súčinu viacerých faktorov sa rovná súčinu korene týchto faktorov:

2. Koreň pomeru sa rovná pomeru koreňov dividendy a deliteľa:

3. Pri povýšení koreňa na silu stačí povýšiť na túto silu koreňové číslo:

4. Ak zvýšime stupeň koreňa v m raz a súčasne zvýšiť na m mocnina je číslo odmocniny, potom sa hodnota odmocniny nezmení:

5. Ak znížime stupeň zakorenenia v m extrahujte koreň raz a súčasne m stupňa od radikálneho čísla, potom hodnota koreňa nie je zmení sa:

Rozšírenie pojmu stupeň. Doteraz sme uvažovali o stupňoch len s prirodzeným ukazovateľom; ale akcie stupne a korene môžu viesť aj k negatívne, nula a zlomkové ukazovatele. Všetky tieto exponenty vyžadujú dodatočnú definíciu.

Stupeň so záporným exponentom. Mocnina nejakého čísla s negatívny (celý) ukazovateľ je definovaný ako jednotka delená o na mocninu rovnakého čísla s exponentom rovným absolútnej hodnotenegatívny indikátor:

T teraz vzorec a m: a n= a m - n možno použiť nielen nam, viac ako n, ale aj pri m, menej ako n .

PRÍKLAD a 4 :a 7 = a 4 - 7 = a - 3 .

Ak chceme vzoreca m : a n= a m - nbol spravodlivým = n, potrebujeme definíciu nultého stupňa.

Stupeň s nulovým exponentom. Stupeň akéhokoľvek nenulového čísla s nulovým exponentom je 1.

PRÍKLADY. 2 0 = 1, ( – 5) 0 = 1, (– 3 / 5) 0 = 1.

Stupeň so zlomkovým exponentom. Zvýšiť skutočné číslo a na mocninu m / n , musíte extrahovať koreň n-tý výkon z m mocnina tohto čísla a:

O výrazoch, ktoré nedávajú zmysel. Existuje niekoľko takýchto výrazov.ľubovoľné číslo.

V skutočnosti, ak predpokladáme, že tento výraz sa rovná nejakému číslu X, potom podľa definície operácie delenia máme: 0 = 0 X. Ale táto rovnosť platí ľubovoľné číslo x, čo malo byť preukázané.

Prípad 3

0 0 - ľubovoľné číslo.

naozaj,

Riešenie. Zvážte tri hlavné prípady:

1) X = 0 – táto hodnota nespĺňa túto rovnicu

(Prečo?).

2) kedy X> 0 dostaneme: x / x = 1, t.j. 1 = 1, odkiaľ nasleduje,

čo X- ľubovoľné číslo; ale s prihliadnutím na to

Náš prípad X> 0, odpoveď jeX > 0 ;

3) kedy X < 0 получаем: – x / x= 1, t.j . –1 = 1, teda

V tomto prípade neexistuje riešenie.

Touto cestou, X > 0.

Pomerne často sa pri riešení problémov stretávame s veľkými číslami, z ktorých musíme vyťažiť Odmocnina. Mnohí žiaci sa rozhodnú, že ide o omyl a začnú riešiť celý príklad. V žiadnom prípade by sa to nemalo robiť! Sú na to dva dôvody:

1. Korene veľkého počtu sa vyskytujú v problémoch. Najmä v texte;
2. Existuje algoritmus, podľa ktorého sa tieto korene zvažujú takmer verbálne.

Tento algoritmus dnes zvážime. Možno sa vám niektoré veci budú zdať nepochopiteľné. Ale ak budete venovať pozornosť tejto lekcii, dostanete najsilnejšiu zbraň proti odmocniny.

Takže algoritmus:

1. Obmedzte požadovaný koreň nad a pod na násobky 10. Takto zmenšíme rozsah vyhľadávania na 10 čísel;
2. Z týchto 10 čísel vyraďte tie, ktoré rozhodne nemôžu byť koreňmi. V dôsledku toho zostanú 1-2 čísla;
3. Odmocni tieto 1-2 čísla. Tá z nich, ktorých druhá mocnina sa rovná pôvodnému číslu, bude odmocninou.

Pred aplikáciou tohto algoritmu v praxi sa pozrime na každý jednotlivý krok.

Koreňové obmedzenie

V prvom rade musíme zistiť, medzi ktorými číslami sa nachádza náš koreň. Je veľmi žiaduce, aby čísla boli násobkom desiatich:

10 2 = 100;
20 2 = 400;
30 2 = 900;
40 2 = 1600;
...
90 2 = 8100;
100 2 = 10 000.

Dostaneme sériu čísel:

100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.

Čo nám tieto čísla dávajú? Je to jednoduché: dostávame hranice. Vezmime si napríklad číslo 1296. Leží medzi 900 a 1600. Preto jeho koreň nemôže byť menší ako 30 a väčší ako 40:

[Titul obrázku]

To isté platí pre akékoľvek iné číslo, z ktorého môžete nájsť druhú odmocninu. Napríklad 3364:

[Titul obrázku]

Namiesto nezrozumiteľného čísla tak dostaneme veľmi špecifický rozsah, v ktorom leží pôvodný koreň. Ak chcete ďalej zúžiť rozsah vyhľadávania, prejdite na druhý krok.

Eliminácia zjavne nadbytočných čísel

Takže máme 10 čísel - kandidátov na koreň. Dostali sme ich veľmi rýchlo, bez zložitého premýšľania a násobenia v kolónke. Je čas pohnúť sa.

Verte či neverte, teraz zredukujeme počet kandidátskych čísel na dve – a opäť bez zložitých výpočtov! Stačí poznať špeciálne pravidlo. Tu je:

Posledná číslica štvorca závisí len od poslednej číslice pôvodné číslo.

Inými slovami, stačí sa pozrieť na poslednú číslicu štvorca – a hneď pochopíme, kde končí pôvodné číslo.

Na poslednom mieste môže byť iba 10 číslic. Pokúsme sa zistiť, na čo sa premenia, keď sú štvorcové. Pozrite sa na tabuľku:

1	2	3	4	5	6	7	8	9	0
1	4	9	6	5	6	9	4	1	0

Táto tabuľka je ďalším krokom k výpočtu koreňa. Ako vidíte, čísla v druhom riadku sa ukázali ako symetrické vzhľadom na päť. Napríklad:

2 2 = 4;
8 2 = 64 → 4.

Ako vidíte, posledná číslica je v oboch prípadoch rovnaká. A to znamená, že napríklad koreň 3364 nevyhnutne končí na 2 alebo 8. Na druhej strane si pamätáme obmedzenie z predchádzajúceho odseku. Dostaneme:

[Titul obrázku]

Červené štvorce ukazujú, že tento údaj ešte nepoznáme. Ale koniec koncov, koreň leží medzi 50 a 60, na ktorých sú len dve čísla končiace na 2 a 8:

[Titul obrázku]

To je všetko! Zo všetkých možných koreňov sme nechali len dve možnosti! A to je v najťažšom prípade, pretože posledná číslica môže byť 5 alebo 0. A potom zostane jediným kandidátom na korene!

Záverečné výpočty

Zostali nám teda 2 čísla kandidátov. Ako viete, ktorý z nich je koreň? Odpoveď je zrejmá: odmocni obe čísla. Ten, ktorý odmocni, dá pôvodné číslo a bude odmocninou.

Napríklad pre číslo 3364 sme našli dve kandidátske čísla: 52 a 58. Odmocnime ich:

52 2 \u003d (50 +2) 2 \u003d 2500 + 2 50 2 + 4 \u003d 2704;
58 2 \u003d (60 - 2) 2 \u003d 3600 - 2 60 2 + 4 \u003d 3364.

To je všetko! Ukázalo sa, že koreň je 58! Zároveň som pre zjednodušenie výpočtov použil vzorec druhých mocnín súčtu a rozdielu. Vďaka tomu ste ani nemuseli násobiť čísla v stĺpci! Toto je ďalšia úroveň optimalizácie výpočtov, ale, samozrejme, je úplne voliteľná :)

Príklady výpočtu koreňa

Teória je dobrá, samozrejme. Poďme si to však vyskúšať v praxi.

[Titul obrázku]

Najprv zistíme, medzi ktorými číslami leží číslo 576:

400 < 576 < 900
20 2 < 576 < 30 2

Teraz sa pozrime na posledné číslo. Rovná sa 6. Kedy sa to stane? Iba ak koreň končí na 4 alebo 6. Získame dve čísla:

Zostáva odmocniť každé číslo a porovnať s originálom:

24 2 = (20 + 4) 2 = 576

Výborne! Ukázalo sa, že prvý štvorec sa rovná pôvodnému číslu. Takže toto je koreň.

Úloha. Vypočítajte druhú odmocninu:

[Titul obrázku]

900 < 1369 < 1600;
30 2 < 1369 < 40 2;

Pozrime sa na posledné číslo:

1369 → 9;
33; 37.

Urobme to na druhú:

33 2 \u003d (30 + 3) 2 \u003d 900 + 2 30 3 + 9 \u003d 1089 ≠ 1369;
37 2 \u003d (40 - 3) 2 \u003d 1600 - 2 40 3 + 9 \u003d 1369.

Tu je odpoveď: 37.

Úloha. Vypočítajte druhú odmocninu:

[Titul obrázku]

Obmedzujeme počet:

2500 < 2704 < 3600;
50 2 < 2704 < 60 2;

Pozrime sa na posledné číslo:

2704 → 4;
52; 58.

Urobme to na druhú:

52 2 = (50 + 2) 2 = 2500 + 2 50 2 + 4 = 2704;

Dostali sme odpoveď: 52. Druhé číslo už nebude potrebné odmocňovať.

Úloha. Vypočítajte druhú odmocninu:

[Titul obrázku]

Obmedzujeme počet:

3600 < 4225 < 4900;
60 2 < 4225 < 70 2;

Pozrime sa na posledné číslo:

4225 → 5;
65.

Ako vidíte, po druhom kroku zostáva iba jedna možnosť: 65. Toto je požadovaný koreň. Ale dajme si to na druhú a skontrolujte:

65 2 = (60 + 5) 2 = 3600 + 2 60 5 + 25 = 4225;

Všetko je správne. Odpoveď zapíšeme.

Záver

Bohužiaľ, o nič lepšie. Poďme sa pozrieť na dôvody. Sú dve z nich:

• Je zakázané používať kalkulačky pri akejkoľvek bežnej matematickej skúške, či už ide o GIA alebo jednotnú štátnu skúšku. A za nosenie kalkulačky do triedy môžu byť ľahko vyhodení zo skúšky.
• Nebuďte ako hlúpi Američania. Ktoré nie sú ako odmocniny – nedokážu sčítať dve prvočísla. A pri pohľade na zlomky sú vo všeobecnosti hysterické.

Prítomnosť druhých odmocnín vo výraze komplikuje proces delenia, existujú však pravidlá, podľa ktorých je práca so zlomkami oveľa jednoduchšia.

Jediná vec, ktorú musíte mať neustále na pamäti- radikálne výrazy sa delia na radikálne výrazy a faktory na faktory. V procese delenia druhých odmocnín zjednodušíme zlomok. Pamätajte tiež, že koreň môže byť v menovateli.

Metóda 1. Delenie radikálových výrazov

Akčný algoritmus:

Napíšte zlomok

Ak výraz nie je znázornený zlomkom, je potrebné ho zapísať takto, pretože je jednoduchšie dodržať princíp delenia odmocnín.

Príklad 1

144 ÷ 36 , tento výraz by sa mal prepísať takto: 144 36

Použite jeden koreňový znak

Ak čitateľ aj menovateľ obsahujú druhé odmocniny, je potrebné napísať ich koreňové výrazy pod rovnakým koreňovým znamienkom, aby sa uľahčil proces riešenia.

Pripomíname, že radikálny výraz (alebo číslo) je výraz pod koreňovým znakom.

Príklad 2

144 36. Tento výraz by mal byť napísaný takto: 144 36

Rozdeliť koreňové výrazy

Stačí rozdeliť jeden výraz druhým a výsledok zapísať pod znamienko koreňa.

Príklad 3

144 36 = 4 , tento výraz zapíšeme takto: 144 36 = 4

Zjednodušte radikálny výraz (ak je to potrebné)

Ak je koreňový výraz alebo jeden z faktorov dokonalý štvorec, zjednodušte tento výraz.

Pripomeňme si, že dokonalý štvorec je číslo, ktoré je druhou mocninou nejakého celého čísla.

Príklad 4

4 je dokonalý štvorec, pretože 2 × 2 = 4. Preto:

4 = 2 × 2 = 2. Preto 144 36 = 4 = 2 .

Metóda 2. Rozklad výrazu radikálu na faktory

Akčný algoritmus:

Napíšte zlomok

Prepíšte výraz ako zlomok (ak je takto reprezentovaný). To značne zjednodušuje proces delenia výrazov odmocninou, najmä pri faktorizácii.

Príklad 5

8 ÷ 36, prepíšte takto 8 36

Faktorizujte každý z radikálnych výrazov

Faktor číslo pod koreň, ako každé iné celé číslo, píšte len faktory pod znamienko koreňa.

Príklad 6

8 36 = 2 x 2 x 2 6 x 6

Zjednodušte čitateľa a menovateľa zlomku

Aby ste to dosiahli, musíte z koreňového znaku vybrať faktory, ktoré sú plné štvorce. Faktor koreňového vyjadrenia sa teda stáva faktorom pred koreňovým znakom.

Príklad 7

2 2 6 6 × 6 2 × 2 × 2, z toho: 8 36 = 2 2 6

Racionalizujte menovateľa (zbavte sa koreňa)

V matematike existujú pravidlá, podľa ktorých ponechanie koreňa v menovateli je znakom nevkusu, t.j. je zakázané. Ak je v menovateli odmocnina, tak sa jej zbavte.

Vynásobte čitateľa a menovateľa druhou odmocninou, ktorej sa chcete zbaviť.

Príklad 8

Vo výraze 6 2 3 musíte vynásobiť čitateľa a menovateľa 3, aby ste sa ho zbavili v menovateli:

6 2 3 × 3 3 = 6 2 × 3 3 × 3 = 6 6 9 = 6 6 3

Zjednodušte výsledný výraz (ak je to potrebné)

Ak čitateľ a menovateľ obsahujú čísla, ktoré sa môžu a mali by sa znížiť. Zjednodušte také výrazy ako ktorýkoľvek zlomok.

Príklad 9

2 6 zjednodušuje na 1 3 ; takže 2 2 6 sa zjednoduší na 1 2 3 = 2 3

Metóda 3. Delenie druhej odmocniny faktormi

Akčný algoritmus:

Zjednodušte multiplikátory

Pripomeňme, že faktory sú čísla pred koreňovým znakom. Ak chcete faktory zjednodušiť, budete ich musieť rozdeliť alebo znížiť. Nedotýkajte sa koreňových výrazov!

Príklad 10

4 32 6 16 . Najprv znížime 4 6: delíme 2 čitateľa aj menovateľa: 4 6 \u003d 2 3.

Zjednodušte odmocniny

Ak je čitateľ rovnomerne deliteľný menovateľom, potom vydeľte. Ak nie, potom radikálne výrazy zjednodušte ako každé iné.

Príklad 11

32 je rovnomerne deliteľné 16, teda: 32 16 = 2

Vynásobte zjednodušené faktory zjednodušenými koreňmi

Pamätajte na pravidlo: nenechávajte korene v menovateli. Preto jednoducho vynásobíme čitateľa a menovateľa týmto koreňom.

Príklad 12

2 3 × 2 = 2 2 3

Racionalizujte menovateľa (zbavte sa koreňa v menovateli)

Príklad 13

4 3 2 7 . Vynásobte čitateľa a menovateľa číslom 7, aby ste sa zbavili koreňa v menovateli.

4 3 7 × 7 7 = 4 3 × 7 7 × 7 = 4 21 49 = 4 21 7

Metóda 4. Delenie dvojčlenkou s druhou odmocninou

Akčný algoritmus:

Určte, či je v menovateli dvojčlen (binóm).

Pripomeňme, že dvojčlen je výraz, ktorý obsahuje 2 jednočlenné členy. Táto metóda sa používa iba v prípadoch, keď je menovateľom dvojčlen s druhou odmocninou.

Príklad 14

1 5 + 2 - v menovateli je dvojčlenka, keďže sú jednočlenné dva.

Nájdite výraz konjugovaný s binomickým výrazom

Pripomeňme, že konjugovaný dvojčlen je dvojčlen s rovnakými monočlenmi, ale opačnými znamienkami. Ak chcete zjednodušiť výraz a zbaviť sa koreňa v menovateli, mali by ste vynásobiť konjugované dvojčleny.

Príklad 15

5 + 2 a 5 - 2 sú konjugované binómy.

Vynásobte čitateľa a menovateľa dvojčlenkou, ktorá je spojená s dvojčlenkou v menovateli

Táto možnosť vám pomôže zbaviť sa odmocniny v menovateli, pretože súčin konjugovaných dvojčlenov sa rovná rozdielu druhých mocnín každého dvojčlenného členu: (a - b) (a + b) = a 2 - b 2

Príklad 16

1 5 + 2 = 1 (5 - 2) (5 - 2) (5 + 2) = 5 - 2 (5 2 - (2) 2 = 5 - 2 25 - 2 = 5 - 2 23 .

Z toho vyplýva: 1 5 + 2 = 5 - 2 23 .

Tipy:

1. Ak pracujete s druhými odmocninami zmiešaných čísel, preveďte ich na nesprávny zlomok.
2. Rozdiel medzi sčítaním a odčítaním od delenia je v tom, že radikálne výrazy v prípade delenia sa neodporúčajú zjednodušovať (kvôli plným štvorcom).
3. Nikdy (!) nenechávajte koreň v menovateli.
4. Žiadne desatinné miesta alebo zmiešané pred koreňom - ​​musíte ich previesť na obyčajný zlomok a potom zjednodušiť.
5. Je menovateľ súčtom alebo rozdielom dvoch monomílov? Vynásobte takýto dvojčlen jeho združeným dvojčlenom a zbavte sa odmocniny v menovateli.

Ak si všimnete chybu v texte, zvýraznite ju a stlačte Ctrl+Enter

Ak chcete úspešne použiť operáciu extrakcie koreňa v praxi, musíte sa oboznámiť s vlastnosťami tejto operácie.
Všetky vlastnosti sú formulované a preukázané len pre nezáporné hodnoty premenných obsiahnutých v koreňových znakoch.

Veta 1. N-tá odmocnina (n=2, 3, 4,...) súčinu dvoch nezáporných čipsetov sa rovná súčinu n-tej odmocniny týchto čísel:

komentár:

1. Veta 1 zostáva v platnosti pre prípad, keď je radikálový výraz súčinom viac ako dvoch nezáporných čísel.

Veta 2.Ak, a n je prirodzené číslo väčšie ako 1, potom rovnosť

Stručný(hoci nepresná) formulácia, ktorá je v praxi vhodnejšia: koreň zlomku sa rovná zlomku koreňov.

Veta 1 nám umožňuje vynásobiť m len korene rovnakého stupňa , t.j. iba korene s rovnakým exponentom.

Veta 3. Ak ,k je prirodzené číslo a n je prirodzené číslo väčšie ako 1, potom rovnosť

Inými slovami, na pozdvihnutie koreňa k prirodzenej sile stačí povýšiť koreňový výraz na túto silu.
Toto je dôsledok vety 1. Skutočne napríklad pre k = 3 dostaneme

Veta 4. Ak ,k, n sú prirodzené čísla väčšie ako 1, potom rovnosť

Inými slovami, na extrahovanie koreňa z koreňa stačí vynásobiť exponenty koreňov.
Napríklad,

Buď opatrný! Dozvedeli sme sa, že s koreňmi možno vykonať štyri operácie: násobenie, delenie, umocňovanie a extrakciu odmocniny (z koreňa). Ale čo sčítanie a odčítanie koreňov? V žiadnom prípade.
Napríklad nemôžete písať namiesto Skutočne, ale je zrejmé, že

Veta 5. Ak ukazovatele koreňa a koreňového výrazu sa vynásobia alebo vydelia rovnakým prirodzeným číslom, potom sa hodnota koreňa nezmení, t.j.

Príklady riešenia problémov

Príklad 1 Vypočítajte

Riešenie. Pomocou prvej vlastnosti koreňov (veta 1) dostaneme:

Príklad 2 Vypočítajte
Riešenie. Preveďte zmiešané číslo na nesprávny zlomok.
Máme Použitie druhej vlastnosti koreňov ( veta 2 ), dostaneme:

Príklad 3 Vypočítať:

Riešenie. Akýkoľvek vzorec v algebre, ako dobre viete, sa používa nielen „zľava doprava“, ale aj „sprava doľava“. Takže prvá vlastnosť koreňov znamená, že môže byť reprezentovaná ako a naopak môže byť nahradená výrazom. To isté platí pre druhú vlastnosť koreňov. S ohľadom na to urobme výpočty.

Gratulujeme: dnes budeme analyzovať korene - jednu z najzaujímavejších tém 8. ročníka. :)

Mnoho ľudí je zmätených v súvislosti s koreňmi nie preto, že sú zložité (čo je komplikované – pár definícií a pár ďalších vlastností), ale preto, že vo väčšine školských učebníc sú korene definované takými divočinami, že to dokážu len samotní autori učebníc. pochopiť toto čmáranie. A aj to len s fľašou dobrej whisky. :)

Preto teraz uvediem najsprávnejšiu a najkompetentnejšiu definíciu koreňa - jedinú, ktorú si skutočne musíte zapamätať. A až potom vysvetlím: prečo je to všetko potrebné a ako to aplikovať v praxi.

Najprv si však zapamätajte jeden dôležitý bod, na ktorý z nejakého dôvodu mnohí zostavovatelia učebníc „zabudnú“:

Korene môžu byť párneho stupňa (naše obľúbené $\sqrt(a)$, ako aj ľubovoľné $\sqrt(a)$ a párne $\sqrt(a)$) a nepárne (ľubovoľné $\sqrt(a)$ , $\ sqrt(a)$ atď.). A definícia koreňa nepárneho stupňa je trochu odlišná od párneho.

Tu v tomto skurvenom „trochu iné“ sa skrýva pravdepodobne 95% všetkých chýb a nedorozumení spojených s koreňmi. Poďme si teda raz a navždy ujasniť terminológiu:

Definícia. Dokonca aj koreň n od čísla $a$ je ľubovoľný nezápornéčíslo $b$ také, že $((b)^(n))=a$. A koreň nepárneho stupňa z rovnakého čísla $a$ je vo všeobecnosti akékoľvek číslo $b$, pre ktoré platí rovnaká rovnosť: $((b)^(n))=a$.

V každom prípade je koreň označený takto:

\(a)\]

Číslo $n$ v takomto zápise sa nazýva koreňový exponent a číslo $a$ sa nazýva radikálny výraz. Konkrétne, pre $n=2$ dostaneme našu „obľúbenú“ druhú odmocninu (mimochodom, toto je odmocnina párneho stupňa) a pre $n=3$ dostaneme kubickú odmocninu (nepárny stupeň), ktorý sa tiež často nachádza v úlohách a rovniciach.

Príklady. Klasické príklady odmocnin:

\[\begin(align) & \sqrt(4)=2; \\ & \sqrt(81)=9; \\ & \sqrt(256)=16. \\ \end(zarovnať)\]

Mimochodom, $\sqrt(0)=0$ a $\sqrt(1)=1$. Je to celkom logické, keďže $((0)^(2))=0$ a $((1)^(2))=1$.

Časté sú aj kubické korene - nebojte sa ich:

\[\begin(align) & \sqrt(27)=3; \\ & \sqrt(-64)=-4; \\ & \sqrt(343)=7. \\ \end(zarovnať)\]

No, pár "exotických príkladov":

\[\begin(align) & \sqrt(81)=3; \\ & \sqrt(-32)=-2. \\ \end(zarovnať)\]

Ak nerozumiete, aký je rozdiel medzi párnym a nepárnym stupňom, prečítajte si definíciu ešte raz. Je to veľmi dôležité!

Medzitým sa pozrieme na jednu nepríjemnú vlastnosť koreňov, kvôli ktorej sme potrebovali zaviesť samostatnú definíciu pre párne a nepárne exponenty.

Prečo vôbec potrebujeme korene?

Po prečítaní definície sa mnohí študenti opýtajú: „Čo matematici fajčili, keď na to prišli? A naozaj: prečo potrebujeme všetky tieto korene?

Aby sme odpovedali na túto otázku, vráťme sa na chvíľu do základnej školy. Pamätajte: v tých vzdialených časoch, keď boli stromy zelenšie a halušky chutnejšie, nám išlo hlavne o to správne vynásobiť čísla. No niečo v duchu „päť na päť – dvadsaťpäť“, to je všetko. Čísla však môžete násobiť nie v pároch, ale v trojiciach, štvoriciach a vo všeobecnosti v celých súboroch:

\[\začiatok(zarovnanie) & 5\cdot 5=25; \\ & 5\cdot 5\cdot 5=125; \\ & 5\cdot 5\cdot 5\cdot 5=625; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5=3125; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5=15\ 625. \end(align)\]

O to však nejde. Trik je iný: matematici sú leniví ľudia, preto museli násobenie desiatich pätiek zapísať takto:

Tak prišli na rad. Prečo nenapísať počet faktorov ako horný index namiesto dlhého reťazca? Ako tento:

Je to veľmi pohodlné! Všetky výpočty sa niekoľkonásobne zredukujú a nemôžete minúť kopu pergamenových zošitov na zapísanie nejakých 5 183 . Takýto záznam sa nazýval stupeň čísla, našlo sa v ňom veľa vlastností, ale šťastie sa ukázalo byť krátkodobé.

Po grandióznom chlastaní, ktoré bolo zorganizované len o „objavení“ stupňov, sa nejaký obzvlášť ukameňovaný matematik zrazu opýtal: „Čo ak poznáme stupeň čísla, ale nepoznáme samotné číslo? V skutočnosti, ak vieme, že napríklad určité číslo $b$ dáva 243 5. mocnine, ako potom môžeme uhádnuť, čomu sa rovná samotné číslo $b$?

Tento problém sa ukázal byť oveľa globálnejší, ako by sa na prvý pohľad mohlo zdať. Pretože sa ukázalo, že pre väčšinu „hotových“ stupňov takéto „počiatočné“ čísla neexistujú. Veď posúďte sami:

\[\začiatok(zarovnanie) & ((b)^(3))=27\šípka doprava b=3\cbodka 3\cbodka 3\šípka doprava b=3; \\ & ((b)^(3))=64\šípka doprava b=4\cbodka 4\cbodka 4\šípka doprava b=4. \\ \end(zarovnať)\]

Čo ak $((b)^(3))=50 $? Ukazuje sa, že musíte nájsť určité číslo, ktoré, keď sa vynásobí trikrát, nám dá 50. Čo je to však za číslo? Je jednoznačne väčšie ako 3, pretože 3 3 = 27< 50. С тем же успехом оно меньше 4, поскольку 4 3 = 64 >50. T.j. toto číslo leží niekde medzi tromi a štyrmi, ale čomu sa rovná - Obr pochopíte.

To je presne dôvod, prečo matematici prišli s $n$-tým koreňom. Preto bola predstavená radikálna ikona $\sqrt(*)$. Na označenie rovnakého čísla $b$, ktoré nám pri zadanej mocnine poskytne predtým známu hodnotu

\[\sqrt[n](a)=b\šípka doprava ((b)^(n))=a\]

Netvrdím: tieto korene sa často ľahko zvažujú - vyššie sme videli niekoľko takýchto príkladov. Ale aj tak, vo väčšine prípadov, ak si spomeniete na ľubovoľné číslo a potom sa z neho pokúsite extrahovať koreň ľubovoľného stupňa, čaká vás krutý problém.

Čo je tam! Dokonca ani najjednoduchšie a najznámejšie $\sqrt(2)$ nemôže byť reprezentované v našej bežnej forme - ako celé číslo alebo zlomok. A ak zadáte toto číslo do kalkulačky, uvidíte toto:

\[\sqrt(2)=1,414213562...\]

Ako vidíte, za desatinnou čiarkou je nekonečná postupnosť čísel, ktoré sa neriadia žiadnou logikou. Toto číslo môžete samozrejme zaokrúhliť, aby ste ho mohli rýchlo porovnať s inými číslami. Napríklad:

\[\sqrt(2)=1,4142...\približne 1,4 \lt 1,5\]

Alebo tu je ďalší príklad:

\[\sqrt(3)=1,73205...\približne 1,7 \gt 1,5\]

Ale všetky tieto zaoblenia sú po prvé dosť hrubé; a po druhé, musíte vedieť pracovať aj s približnými hodnotami, inak môžete zachytiť kopu nezjavných chýb (mimochodom, zručnosť porovnávania a zaokrúhľovania sa nevyhnutne kontroluje na profilovej skúške).

Preto sa v serióznej matematike bez koreňov nezaobídeme – sú to rovnakí rovnakí zástupcovia množiny všetkých reálnych čísel $\mathbb(R)$, ako zlomky a celé čísla, ktoré už dávno poznáme.

Nemožnosť reprezentovať koreň ako zlomok tvaru $\frac(p)(q)$ znamená, že tento koreň nie je racionálne číslo. Takéto čísla sa nazývajú iracionálne a nemožno ich presne znázorniť inak ako pomocou radikálu alebo iných špeciálne na to navrhnutých konštrukcií (logaritmy, stupne, limity atď.). Ale o tom viac inokedy.

Zvážte niekoľko príkladov, kde po všetkých výpočtoch zostanú v odpovedi stále iracionálne čísla.

\[\begin(align) & \sqrt(2+\sqrt(27))=\sqrt(2+3)=\sqrt(5)\cca 2 236... \\ & \sqrt(\sqrt(-32) ))=\sqrt(-2)\približne -1,2599... \\ \end(align)\]

Prirodzene, podľa vzhľadu koreňa je takmer nemožné uhádnuť, ktoré čísla budú nasledovať za desatinnou čiarkou. Dá sa však počítať na kalkulačke, no aj tá najpokročilejšia dátumová kalkulačka nám dá len prvých pár číslic iracionálneho čísla. Preto je oveľa správnejšie písať odpovede ako $\sqrt(5)$ a $\sqrt(-2)$.

Na to boli vymyslení. Aby sa vám ľahšie zapisovali odpovede.

Prečo sú potrebné dve definície?

Pozorný čitateľ si už zrejme všimol, že všetky odmocniny uvedené v príkladoch sú prevzaté z kladných čísel. Teda aspoň od nuly. Kocky sú však pokojne extrahované z absolútne ľubovoľného čísla - dokonca aj pozitívneho, dokonca aj negatívneho.

Prečo sa to deje? Pozrite sa na graf funkcie $y=((x)^(2))$:

Graf kvadratickej funkcie dáva dva korene: kladný a záporný

Skúsme vypočítať $\sqrt(4)$ pomocou tohto grafu. Na tento účel je na grafe nakreslená vodorovná čiara $y=4$ (označená červenou farbou), ktorá pretína parabolu v dvoch bodoch: $((x)_(1))=2$ a $((x) _(2)) = -2 $. Je to celkom logické, keďže

S prvým číslom je všetko jasné - je kladné, preto je to koreň:

Ale čo potom robiť s druhým bodom? Má tá 4ka dva korene naraz? Ak totiž odmocníme číslo −2, dostaneme aj 4. Prečo teda nenapísať $\sqrt(4)=-2$? A prečo sa učitelia pozerajú na takéto záznamy, akoby ťa chceli zjesť? :)

Problém je v tom, že ak sa neuložia žiadne ďalšie podmienky, štyri budú mať dve odmocniny – kladnú a zápornú. A každé kladné číslo ich bude mať aj dve. Ale záporné čísla nebudú mať vôbec korene - to je možné vidieť z toho istého grafu, pretože parabola nikdy neklesne pod os r, t.j. nenadobúda záporné hodnoty.

Podobný problém sa vyskytuje pre všetky korene s párnym exponentom:

1. Presne povedané, každé kladné číslo bude mať dva korene s párnym exponentom $n$;
2. Zo záporných čísel sa odmocnina s párnym $n$ vôbec nevytiahne.

To je dôvod, prečo definícia párneho koreňa $n$ špecificky stanovuje, že odpoveď musí byť nezáporné číslo. Takto sa zbavíme nejednoznačnosti.

Ale pre nepárnych $n$ takýto problém neexistuje. Aby sme to videli, pozrime sa na graf funkcie $y=((x)^(3))$:

Kubická parabola nadobúda ľubovoľnú hodnotu, takže odmocnina kocky môže byť prevzatá z ľubovoľného čísla

Z tohto grafu možno vyvodiť dva závery:

1. Vetvy kubickej paraboly, na rozdiel od bežnej, idú do nekonečna v oboch smeroch - hore aj dole. Preto, v akejkoľvek výške nakreslíme vodorovnú čiaru, táto čiara sa bude určite pretínať s naším grafom. Preto je možné vždy odobrať odmocninu, absolútne z akéhokoľvek čísla;
2. Okrem toho bude takáto križovatka vždy jedinečná, takže nemusíte premýšľať o tom, ktoré číslo považovať za „správny“ koreň a ktoré bodovať. Preto je definícia koreňov pre nepárny stupeň jednoduchšia ako pre párny (neexistuje požiadavka na nezápornosť).

Škoda, že tieto jednoduché veci nie sú vo väčšine učebníc vysvetlené. Namiesto toho náš mozog začne stúpať so všetkými druhmi aritmetických koreňov a ich vlastností.

Áno, nehovorím: čo je aritmetický koreň - musíte tiež vedieť. A o tom budem podrobne hovoriť v samostatnej lekcii. Dnes si o nej povieme tiež, pretože bez nej by boli všetky úvahy o koreňoch $n$-tej násobnosti neúplné.

Najprv však musíte jasne pochopiť definíciu, ktorú som uviedol vyššie. V opačnom prípade sa vám kvôli hojnosti pojmov začne v hlave taký chaos, že nakoniec nebudete rozumieť vôbec ničomu.

A všetko, čo potrebujete pochopiť, je rozdiel medzi párnymi a nepárnymi číslami. Preto opäť zhromaždíme všetko, čo skutočne potrebujete vedieť o koreňoch:

1. Párny koreň existuje len od nezáporného čísla a sám je vždy nezáporným číslom. Pre záporné čísla nie je takýto koreň definovaný.
2. Ale koreň nepárneho stupňa existuje z ľubovoľného čísla a sám môže byť ľubovoľným číslom: pre kladné čísla je kladný a pre záporné čísla, ako naznačuje viečko, záporný.

Je to zložité? Nie, nie je to ťažké. Jasný? Áno, je to zrejmé! Preto si teraz trochu precvičíme s výpočtami.

Základné vlastnosti a obmedzenia

Korene majú veľa zvláštnych vlastností a obmedzení - toto bude samostatná lekcia. Preto teraz zvážime iba najdôležitejší "čip", ktorý sa vzťahuje iba na korene s párnym exponentom. Túto vlastnosť zapíšeme vo forme vzorca:

\[\sqrt(((x)^(2n)))=\left| x\vpravo|\]

Inými slovami, ak umocníme číslo na párnu mocninu a potom z neho vyberieme odmocninu rovnakého stupňa, nedostaneme pôvodné číslo, ale jeho modul. Toto je jednoduchá veta, ktorá sa dá ľahko dokázať (stačí zvážiť samostatne nezáporné $x$ a potom samostatne zvážiť negatívne). Učitelia o tom neustále hovoria, je to uvedené v každej školskej učebnici. No akonáhle príde na riešenie iracionálnych rovníc (t. j. rovníc obsahujúcich znamienko radikálu), žiaci tento vzorec razom zabudnú.

Aby sme problém pochopili dopodrobna, zabudnime na minútu všetky vzorce a skúsme spočítať dve čísla dopredu:

\[\sqrt(((3)^(4)))=?\quad \sqrt(((\left(-3 \right))^(4)))=?\]

Toto sú veľmi jednoduché príklady. Prvý príklad bude vyriešený väčšinou ľudí, ale na druhý sa mnohí držia. Aby ste takéto svinstvo vyriešili bez problémov, vždy zvážte postup:

1. Najprv sa číslo zvýši na štvrtú mocninu. No je to akési jednoduché. Získa sa nové číslo, ktoré možno dokonca nájsť v tabuľke násobenia;
2. A teraz z tohto nového čísla je potrebné extrahovať koreň štvrtého stupňa. Tie. nedochádza k "zníženiu" koreňov a stupňov - ide o postupné akcie.

Poďme sa zaoberať prvým výrazom: $\sqrt(((3)^(4)))$. Je zrejmé, že najprv musíte vypočítať výraz pod koreňom:

\[((3)^(4))=3\cdot 3\cdot 3\cdot 3=81\]

Potom extrahujeme štvrtý koreň čísla 81:

Teraz urobme to isté s druhým výrazom. Najprv zvýšime číslo −3 na štvrtú mocninu, pre ktorú ho musíme vynásobiť 4-krát:

\[((\left(-3 \right))^(4))=\left(-3 \right)\cdot \left(-3 \right)\cdot \left(-3 \right)\cdot \ vľavo(-3 \vpravo)=81\]

Dostali sme kladné číslo, keďže celkový počet mínusov v produkte sú 4 kusy a všetky sa navzájom vyrušia (napokon mínus o mínus dáva plus). Potom znova extrahujte koreň:

Tento riadok sa v zásade nedal napísať, keďže je nemysliteľné, že odpoveď bude rovnaká. Tie. párny koreň tej istej párnej sily „vypáli“ mínusy a v tomto zmysle je výsledok nerozoznateľný od bežného modulu:

\[\begin(align) & \sqrt(((3)^(4)))=\left| 3\vpravo|=3; \\ & \sqrt(((\left(-3 \right))^(4)))=\left| -3 \vpravo|=3. \\ \end(zarovnať)\]

Tieto výpočty sú v dobrej zhode s definíciou odmocniny párneho stupňa: výsledok je vždy nezáporný a radikálne znamienko je tiež vždy nezáporné číslo. V opačnom prípade nie je koreň definovaný.

Poznámka k poradiu operácií

1. Zápis $\sqrt(((a)^(2)))$ znamená, že najprv odmocníme číslo $a$ a potom vezmeme druhú odmocninu z výslednej hodnoty. Preto si môžeme byť istí, že nezáporné číslo vždy leží pod znamienkom koreňa, pretože $((a)^(2))\ge 0$ aj tak;
2. No zápis $((\left(\sqrt(a) \right))^(2))$ naopak znamená, že najskôr vytiahneme odmocninu z určitého čísla $a$ a až potom výsledok odmocníme. Preto číslo $a$ v žiadnom prípade nemôže byť záporné - je to povinná požiadavka zakotvená v definícii.

V žiadnom prípade by sa teda nemali bezmyšlienkovite zmenšovať korene a stupne, čím sa vraj „zjednodušuje“ pôvodný výraz. Pretože ak je pod odmocninou záporné číslo a jeho exponent je párny, dostaneme veľa problémov.

Všetky tieto problémy sú však relevantné len pre párne ukazovatele.

Odstránenie znamienka mínus spod koreňového znamienka

Prirodzene, korene s nepárnymi exponentmi majú tiež svoju vlastnosť, ktorá v zásade neexistuje pre párne. menovite:

\[\sqrt(-a)=-\sqrt(a)\]

Stručne povedané, môžete vytiahnuť mínus pod znakom koreňov nepárneho stupňa. Toto je veľmi užitočná vlastnosť, ktorá vám umožní „vyhodiť“ všetky mínusy:

\[\begin(align) & \sqrt(-8)=-\sqrt(8)=-2; \\ & \sqrt(-27)\cdot \sqrt(-32)=-\sqrt(27)\cdot \left(-\sqrt(32) \right)= \\ & =\sqrt(27)\cdot \sqrt(32)= \\ & =3\cdot 2=6. \end(align)\]

Táto jednoduchá vlastnosť výrazne zjednodušuje mnohé výpočty. Teraz sa už nemusíte obávať: čo ak sa negatívny výraz dostal pod koreň a stupeň pri koreni sa ukázal byť párny? Všetky mínusy stačí „vyhodiť“ mimo koreňov, potom sa môžu navzájom množiť, deliť a celkovo robiť veľa podozrivých vecí, ktoré nás v prípade „klasických“ koreňov zaručene privedú k omylu. .

A tu vstupuje na scénu ďalšia definícia – práve tá, s ktorou väčšina škôl začína štúdium iracionálnych výrazov. A bez toho by naša úvaha bola neúplná. Zoznámte sa!

aritmetický koreň

Predpokladajme na chvíľu, že pod znamienkom koreňa môžu byť iba kladné čísla alebo v extrémnych prípadoch nula. Bodujme na párnych / nepárnych ukazovateľoch, bodujme na všetkých vyššie uvedených definíciách - budeme pracovať len s nezápornými číslami. Čo potom?

A potom dostaneme aritmetický koreň - čiastočne sa pretína s našimi "štandardnými" definíciami, ale stále sa od nich líši.

Definícia. Aritmetický koreň $n$-tého stupňa nezáporného čísla $a$ je nezáporné číslo $b$ také, že $((b)^(n))=a$.

Ako vidíte, parita nás už nezaujíma. Namiesto toho sa objavilo nové obmedzenie: radikálny výraz je teraz vždy nezáporný a samotný koreň je tiež nezáporný.

Aby ste lepšie pochopili, ako sa aritmetický koreň líši od bežného, ​​pozrite sa na grafy štvorcovej a kubickej paraboly, ktoré už poznáme:

Oblasť vyhľadávania koreňov - nezáporné čísla

Ako vidíte, odteraz nás zaujímajú len tie časti grafov, ktoré sa nachádzajú v prvej súradnicovej štvrtine – kde sú súradnice $x$ a $y$ kladné (alebo aspoň nulové). Už sa nemusíte pozerať na indikátor, aby ste pochopili, či máme právo odmocniť záporné číslo alebo nie. Pretože so zápornými číslami sa už v zásade nepočíta.

Môžete sa opýtať: "No, prečo potrebujeme takú kastrovanú definíciu?" Alebo: "Prečo si nemôžeme vystačiť so štandardnou definíciou uvedenou vyššie?"

Uvediem len jednu vlastnosť, kvôli ktorej sa nová definícia stáva vhodnou. Napríklad pravidlo umocňovania:

\[\sqrt[n](a)=\sqrt(((a)^(k)))\]

Poznámka: radikálny výraz môžeme zvýšiť na ľubovoľnú mocninu a zároveň vynásobiť koreňový exponent rovnakou mocninou – a výsledkom bude rovnaké číslo! Tu je niekoľko príkladov:

\[\begin(align) & \sqrt(5)=\sqrt(((5)^(2)))=\sqrt(25) \\ & \sqrt(2)=\sqrt(((2)^ (4)))=\sqrt(16) \\ \end(align)\]

No čo je na tom zlé? Prečo sme to nemohli urobiť skôr? Tu je dôvod. Uvažujme jednoduchý výraz: $\sqrt(-2)$ je číslo, ktoré je v našom klasickom zmysle celkom normálne, ale z hľadiska aritmetického koreňa absolútne neprijateľné. Skúsme to previesť:

$\begin(align) & \sqrt(-2)=-\sqrt(2)=-\sqrt(((2)^(2)))=-\sqrt(4) \lt 0; \\ & \sqrt(-2)=\sqrt(((\left(-2 \right))^(2)))=\sqrt(4) \gt 0. \\ \end(align)$

Ako vidíte, v prvom prípade sme vybrali mínus spod radikálu (máme plné právo, pretože indikátor je nepárny) av druhom prípade sme použili vyššie uvedený vzorec. Tie. z pohľadu matematiky sa všetko robí podľa pravidiel.

WTF?! Ako môže byť rovnaké číslo kladné aj záporné? V žiadnom prípade. Ide len o to, že vzorec umocňovania, ktorý funguje skvele pre kladné čísla a nulu, začína v prípade záporných čísel dávať úplnú herézu.

Tu, aby sa zbavili takejto nejednoznačnosti, prišli s aritmetickými koreňmi. Je im venovaná samostatná veľká lekcia, kde podrobne zvážime všetky ich vlastnosti. Takže teraz sa nimi nebudeme zaoberať - lekcia sa aj tak ukázala ako príliš dlhá.

Algebraický koreň: pre tých, ktorí chcú vedieť viac

Dlho som premýšľal: urobiť túto tému v samostatnom odseku alebo nie. Nakoniec som sa rozhodol odísť odtiaľto. Tento materiál je určený pre tých, ktorí chcú ešte lepšie pochopiť korene - už nie na priemernej „školskej“ úrovni, ale na úrovni blízkej olympiáde.

Takže: okrem „klasickej“ definície koreňa $n$-tého stupňa z čísla a s tým spojeného delenia na párne a nepárne ukazovatele existuje aj „dospelejšia“ definícia, ktorá nezávisí od parity a iné jemnosti vôbec. Toto sa nazýva algebraický koreň.

Definícia. Algebraická $n$-tá odmocnina ľubovoľného $a$ je množina všetkých čísel $b$ takých, že $((b)^(n))=a$. Pre takéto korene neexistuje dobre zavedené označenie, takže navrch stačí dať pomlčku:

\[\overline(\sqrt[n](a))=\vľavo\( b\vľavo| b\v \mathbb(R);((b)^(n))=a \vpravo. \vpravo\) \]

Zásadný rozdiel oproti štandardnej definícii uvedenej na začiatku lekcie je v tom, že algebraický koreň nie je konkrétne číslo, ale množina. A keďže pracujeme s reálnymi číslami, táto množina je len troch typov:

1. Prázdna súprava. Vyskytuje sa, keď je potrebné nájsť algebraický koreň párneho stupňa zo záporného čísla;
2. Sada pozostávajúca z jedného prvku. Do tejto kategórie spadajú všetky korene nepárnych mocnín, ako aj odmocniny párnych mocnín od nuly;
3. Nakoniec môže množina obsahovať dve čísla – rovnaké $((x)_(1))$ a $((x)_(2))=-((x)_(1))$, ktoré sme videli na graf kvadratická funkcia. V súlade s tým je takéto zarovnanie možné len pri extrakcii odmocniny párneho stupňa z kladného čísla.

Posledný prípad si zaslúži podrobnejšie posúdenie. Poďme si spočítať pár príkladov, aby sme pochopili rozdiel.

Príklad. Vypočítajte výrazy:

\[\overline(\sqrt(4));\quad \overline(\sqrt(-27));\quad \overline(\sqrt(-16)).\]

Riešenie. Prvý výraz je jednoduchý:

\[\overline(\sqrt(4))=\left\( 2;-2 \right\)\]

Sú to dve čísla, ktoré sú súčasťou sady. Pretože každá z nich na druhú dáva štvorku.

\[\overline(\sqrt(-27))=\left\( -3 \right\)\]

Tu vidíme množinu pozostávajúcu iba z jedného čísla. Je to celkom logické, keďže exponent odmocniny je nepárny.

Nakoniec posledný výraz:

\[\overline(\sqrt(-16))=\varnothing \]

Máme prázdny set. Pretože neexistuje jediné reálne číslo, ktoré nám po zvýšení na štvrtú (čiže párnu!) mocninu dá záporné číslo −16.

Poznámka na záver. Poznámka: nie náhodou som všade poznamenal, že pracujeme s reálnymi číslami. Pretože existujú aj komplexné čísla - je tam celkom možné vypočítať $\sqrt(-16)$ a mnoho ďalších podivných vecí.

V moderných školských osnovách matematiky sa však komplexné čísla takmer nikdy nenachádzajú. Z väčšiny učebníc boli vynechané, pretože naši úradníci považujú túto tému za „príliš ťažké na pochopenie“.

To je všetko. V ďalšej lekcii sa pozrieme na všetky kľúčové vlastnosti koreňov a nakoniec sa naučíme, ako zjednodušiť iracionálne výrazy. :)