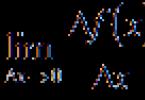Când obținem prima formulă a tabelului, vom porni de la definiția funcției derivate într-un punct. Să luăm unde X– orice număr real, adică X– orice număr din domeniul de definire al funcției. Să notăm limita raportului dintre incrementul funcției și incrementul argumentului la:

De remarcat că sub semnul limită se obține expresia, care nu este incertitudinea zero împărțită la zero, întrucât numărătorul nu conține o valoare infinitezimală, ci exact zero. Cu alte cuvinte, incrementul unei funcții constante este întotdeauna zero.

Prin urmare, derivata unei functii constanteeste egal cu zero în întregul domeniu de definiție.

Derivată a unei funcții de putere.

Formula pentru derivata unei funcții putere are forma , unde exponentul p– orice număr real.

Să demonstrăm mai întâi formula exponentului natural, adică pentru p = 1, 2, 3, …

Vom folosi definiția derivatei. Să notăm limita raportului dintre incrementul unei funcții de putere și incrementul argumentului:

Pentru a simplifica expresia în numărător, ne întoarcem la formula binomială Newton:

Prin urmare,

Aceasta dovedește formula pentru derivata unei funcții de putere pentru un exponent natural.

Derivată a unei funcții exponențiale.

Prezentăm derivarea formulei derivate pe baza definiției:

Am ajuns la incertitudine. Pentru a o extinde, introducem o nouă variabilă, iar la . Apoi . În ultima tranziție, am folosit formula pentru trecerea la o nouă bază logaritmică.

Să înlocuim în limita inițială:

Dacă ne amintim a doua limită remarcabilă, ajungem la formula pentru derivata funcției exponențiale:

Derivată a unei funcții logaritmice.

Să demonstrăm formula pentru derivata unei funcții logaritmice pentru toate X din domeniul definiției și toate valorile valide ale bazei A logaritm Prin definiția derivatei avem:

După cum ați observat, în timpul demonstrației transformările au fost efectuate folosind proprietățile logaritmului. Egalitatea este adevărat datorită celei de-a doua limite remarcabile.

Derivate ale funcţiilor trigonometrice.

Pentru a deriva formule pentru derivate ale funcțiilor trigonometrice, va trebui să reamintim câteva formule de trigonometrie, precum și prima limită remarcabilă.

Prin definiția derivatei pentru funcția sinus avem .

Să folosim formula diferenței sinusurilor:

Rămâne să ne întoarcem la prima limită remarcabilă:

Astfel, derivata funcției sin x Există cos x.

Formula pentru derivata cosinusului este dovedită exact în același mod.

Prin urmare, derivata funcției cos x Există –sin x.

Vom obține formule pentru tabelul de derivate pentru tangentă și cotangentă folosind reguli dovedite de diferențiere (derivată a unei fracții).

Derivate ale funcțiilor hiperbolice.

Regulile de diferențiere și formula pentru derivata funcției exponențiale din tabelul derivatelor ne permit să derivăm formule pentru derivatele sinusului hiperbolic, cosinusului, tangentei și cotangentei.

Derivată a funcției inverse.

Pentru a evita confuzia în timpul prezentării, să notăm în indice argumentul funcției prin care se realizează diferențierea, adică este derivata funcției f(x) De X.

Acum hai să formulăm regula pentru aflarea derivatei unei functii inverse.

Lasă funcțiile y = f(x)Și x = g(y) reciproc invers, definite pe intervale și respectiv. Dacă într-un punct există o derivată finită nenulă a funcției f(x), atunci în punct există o derivată finită a funcției inverse g(y), și . Într-o altă postare .

Această regulă poate fi reformulată pentru oricare X din intervalul , atunci obținem .

Să verificăm validitatea acestor formule.

Să găsim funcția inversă pentru logaritmul natural (Aici y este o funcție și X- argument). După ce am rezolvat această ecuație pt X, primim (aici X este o funcție și y– argumentul ei). Acesta este, și funcții reciproc inverse.

Din tabelul derivatelor vedem că Și .

Să ne asigurăm că formulele pentru găsirea derivatelor funcției inverse ne conduc la aceleași rezultate:

După cum puteți vedea, am obținut aceleași rezultate ca și în tabelul cu derivate.

Acum avem cunoștințele pentru a demonstra formule pentru derivatele funcțiilor trigonometrice inverse.

Să începem cu derivata arcsinusului.

. Apoi, folosind formula pentru derivata funcției inverse, obținem

Tot ce rămâne este să efectuăm transformările.

Deoarece intervalul arcsinus este intervalul , Acea (vezi secțiunea privind funcțiile elementare de bază, proprietățile și graficele acestora). Prin urmare, nu luăm în considerare.

Prin urmare, . Domeniul de definire al derivatei arcsinus este intervalul (-1; 1) .

Pentru arccosinus, totul se face exact în același mod:

Să găsim derivata arctangentei.

Pentru funcția inversă este .

Să exprimăm arctangenta în termeni de arccosin pentru a simplifica expresia rezultată.

Lăsa arctgx = z, Apoi

Prin urmare,

Derivata cotangentei arcului se găsește într-un mod similar:

Procesul de găsire a derivatei unei funcții se numește diferenţiere. Derivata trebuie găsită într-o serie de probleme în cursul analizei matematice. De exemplu, atunci când găsiți puncte extreme și puncte de inflexiune ale unui grafic al funcției.

Cum să găsești?

Pentru a găsi derivata unei funcții trebuie să cunoașteți tabelul derivatelor funcțiilor elementare și să aplicați regulile de bază de diferențiere:

Mutarea constantei dincolo de semnul derivatei: $$ (Cu)" = C(u)" $$
Derivată a sumei/diferenței funcțiilor: $$ (u \pm v)" = (u)" \pm (v)" $$
Derivată a produsului a două funcții: $$ (u \cdot v)" = u"v + uv" $$
Derivată a unei fracții: $$ \bigg (\frac(u)(v) \bigg)" = \frac(u"v - uv"))(v^2) $$
Derivată a unei funcții complexe: $$ (f(g(x)))" = f"(g(x)) \cdot g"(x) $$

Exemple de soluții

Exemplul 1
Aflați derivata funcției $ y = x^3 - 2x^2 + 7x - 1 $
Soluţie
Derivata sumei/diferenței de funcții este egală cu suma/diferenței derivatelor: $$ y" = (x^3 - 2x^2 + 7x - 1)" = (x^3)" - (2x^2)" + (7x)" - (1)" = $$ Folosind regula pentru derivata unei funcții de putere $ (x^p)" = px^(p-1) $ avem: $$ y" = 3x^(3-1) - 2 \cdot 2 x^(2-1) + 7 - 0 = 3x^2 - 4x + 7 $$ S-a mai ținut cont de faptul că derivata unei constante este egală cu zero. Dacă nu vă puteți rezolva problema, trimiteți-ne-o. Vom oferi o soluție detaliată. Veți putea vizualiza progresul calculului și veți obține informații. Acest lucru vă va ajuta să obțineți nota de la profesorul dvs. în timp util!
Răspuns
$$y" = 3x^2 - 4x + 7 $$

CU editarea materialelor pe tema „derivată”. Nivel de școală de bază.
Informații teoretice pentru studenți, profesori și tutori la matematică. Pentru a ajuta la conducerea cursurilor.

Definiție: derivata unei funcții într-un punct este limita raportului dintre incrementul funcției și incrementul variabilei, adică

Tabel de derivate ale funcțiilor matematice de bază:

Reguli pentru calcularea instrumentelor derivate

Derivată a unei sume oricare două expresii este egală cu suma derivatelor acestor expresii (derivata sumei este egală cu suma derivatelor)

Derivată a diferenței oricare două expresii este egală cu diferența derivatelor acestor termeni (derivata diferenței este egală cu diferența derivatelor).

Derivat al produsului doi factori este egal cu produsul derivatei primului factor și al doilea plus produsul primului factor și derivata celui de-al doilea (suma derivatelor factorilor luate pe rând).
Comentariu profesor de matematică: Când îi reamintesc pe scurt unui student despre regula de calcul a derivatei unui produs, spun asta: derivată a primului factor cu al doilea plus schimba lovituri!

Derivată a coeficientului două expresii este egală cu câtul diferenței dintre derivatele factorilor luate pe rând și pătratul numitorului.

Derivată a produsului dintre un număr și o funcție. Pentru a găsi derivata produsului dintre un număr și o expresie literală (funcție), trebuie să înmulțiți acest număr cu derivata acestei expresii literale.

Derivata unei functii complexe:

Pentru a calcula derivata unei funcții complexe, trebuie să găsiți derivata funcției exterioare și să o înmulțiți cu derivata funcției interioare.

Comentariile și feedback-ul dvs. pe pagina de derivate:
Alexandru S.
Chiar aveam nevoie de o masă. Una dintre cele mai multe de pe internet. Multumesc mult si pentru explicatii si reguli. Cel puțin încă un exemplu ar fi grozav pentru ei. Vă mulțumesc foarte mult din nou.

Kolpakov A.N., profesor de matematică: ok, voi încerca să actualizez pagina cu exemple în viitorul apropiat.

Carte virtuală de referință matematică.
Kolpakov Alexander Nikolaevici, profesor de matematică.

Calcul derivat- una dintre cele mai importante operatii din calculul diferential. Mai jos este un tabel pentru găsirea derivatelor funcțiilor simple. Pentru reguli de diferențiere mai complexe, consultați alte lecții:

Tabel de derivate ale funcțiilor exponențiale și logaritmice

Utilizați formulele date ca valori de referință. Acestea vor ajuta la rezolvarea ecuațiilor diferențiale și a problemelor. În imagine, în tabelul de derivate ale funcțiilor simple, există o „foaie de cheat” a principalelor cazuri de găsire a unei derivate într-o formă care este de înțeles pentru utilizare, alături de aceasta sunt explicații pentru fiecare caz.

Derivate ale funcțiilor simple

1. Derivata unui număr este zero
с´ = 0
Exemplu:
5' = 0

Explicaţie:
Derivata arată rata la care valoarea unei funcții se schimbă atunci când argumentul acesteia se schimbă. Deoarece numărul nu se modifică în niciun fel în nicio condiție, rata modificării sale este întotdeauna zero.

2. Derivată a unei variabile egal cu unu
x´ = 1

Explicaţie:
Cu fiecare creștere a argumentului (x) cu unu, valoarea funcției (rezultatul calculului) crește cu aceeași valoare. Astfel, rata de modificare a valorii funcției y = x este exact egală cu rata de modificare a valorii argumentului.

3. Derivata unei variabile si a unui factor este egala cu acest factor
сx´ = с
Exemplu:
(3x)´ = 3
(2x)´ = 2
Explicaţie:
În acest caz, de fiecare dată când argumentul funcției se schimbă ( X) valoarea lui (y) crește în Cu o singura data. Astfel, rata de modificare a valorii funcției în raport cu rata de modificare a argumentului este exact egală cu valoarea Cu.

De unde rezultă că
(cx + b)" = c
adică diferența funcției liniare y=kx+b este egală cu panta dreptei (k).

4. Modul derivată a unei variabile egal cu coeficientul acestei variabile la modulul ei
|x|"= x / |x| cu condiția ca x ≠ 0
Explicaţie:
Deoarece derivata unei variabile (vezi formula 2) este egală cu unu, derivata modulului diferă doar prin aceea că valoarea ratei de modificare a funcției se schimbă în sens opus la trecerea punctului de origine (încercați să desenați un grafic a funcției y = |x| și vedeți singur. Aceasta este exact ce valoare și returnează expresia x / |x|. Când x< 0 оно равно (-1), а когда x >0 - unu. Adică, pentru valorile negative ale variabilei x, cu fiecare creștere a argumentului, valoarea funcției scade cu exact aceeași valoare, iar pentru valorile pozitive, dimpotrivă, crește, dar exact cu aceeași valoare. .

5. Derivată a unei variabile la o putere egal cu produsul unui număr din această putere și o variabilă cu puterea redusă cu unu
(x c)"= cx c-1, cu condiția ca x c și cx c-1 să fie definite și c ≠ 0
Exemplu:
(x 2)" = 2x
(x 3)" = 3x 2
Pentru a reține formula:
Mutați în jos gradul variabilei ca factor, apoi reduceți gradul în sine cu unul. De exemplu, pentru x 2 - cei doi au fost înaintea lui x, iar apoi puterea redusă (2-1 = 1) ne-a dat pur și simplu 2x. Același lucru s-a întâmplat și pentru x 3 - „deplasăm în jos” triplul, îl reducem cu unul și în loc de cub avem un pătrat, adică 3x 2. Puțin „neștiințific”, dar foarte ușor de reținut.

6.Derivată a unei fracții 1/x
(1/x)" = - 1 / x 2
Exemplu:
Deoarece o fracție poate fi reprezentată ca ridicând la o putere negativă
(1/x)" = (x -1)", atunci puteți aplica formula de la regula 5 din tabelul derivatelor
(x -1)" = -1x -2 = - 1 / x 2

7. Derivată a unei fracții cu o variabilă de grad arbitrarîn numitor
(1 / x c)" = - c/x c+1
Exemplu:
(1 / x 2)" = - 2 / x 3

8. Derivat al rădăcinii(derivată a variabilei sub rădăcină pătrată)
(√x)" = 1 / (2√x) sau 1/2 x -1/2
Exemplu:
(√x)" = (x 1/2)" înseamnă că puteți aplica formula de la regula 5
(x 1/2)" = 1/2 x -1/2 = 1 / (2√x)

9. Derivată a unei variabile sub rădăcina unui grad arbitrar
(n √x)" = 1 / (n n √x n-1)

Data: 05/10/2015

Cum să găsesc derivatul?

Reguli de diferențiere.

Pentru a găsi derivata oricărei funcții, trebuie să stăpânești doar trei concepte:

2. Reguli de diferențiere.

3. Derivata unei functii complexe.

Exact în acea ordine. Este un indiciu.)

Desigur, ar fi bine să aveți o idee despre derivate în general). Ce este un derivat și cum se lucrează cu tabelul derivatelor este explicat clar în lecția anterioară. Aici ne vom ocupa de regulile de diferențiere.

Diferențierea este operația de găsire a derivatei. Nu se ascunde nimic mai mult în spatele acestui termen. Acestea. expresii „găsește derivata unei funcții”Și „diferențierea unei funcții”- Este la fel.

Expresie „reguli de diferențiere” se referă la găsirea derivatei din operatii aritmetice. Această înțelegere ajută foarte mult la evitarea confuziei în capul tău.

Să ne concentrăm și să ne amintim toate, toate, toate operațiile aritmetice. Sunt patru). Adunare (suma), scădere (diferență), înmulțire (produs) și împărțire (cot). Iată-le, regulile de diferențiere:

Placa arată cinci reguli asupra patru operatii aritmetice. Nu am fost preschimbat.) Doar că regula 4 este o consecință elementară a regulii 3. Dar este atât de populară încât are sens să o scrii (și să reții!) ca o formulă independentă.

Sub denumirile UȘi V unele (absolut orice!) funcții sunt implicate U(x)Și V(x).

Să ne uităm la câteva exemple. În primul rând - cele mai simple.

Aflați derivata funcției y=sinx - x 2

Aici avem diferență două funcţii elementare. Aplicam regula 2. Vom presupune ca sinx este o functie U, iar x 2 este funcția V. Avem tot dreptul să scriem:

y" = (sinx - x 2)" = (sinx)"- (x 2)"

Este mai bine, nu?) Tot ce rămâne este să găsiți derivatele sinusului și pătratului lui x. Există un tabel de derivate în acest scop. Căutăm doar funcțiile de care avem nevoie în tabel ( sinxȘi x 2), uită-te la ce derivate au și notează răspunsul:

y" = (sinx)" - (x 2)" = cosx - 2x

Asta este. Regula 1 a diferențierii sumelor funcționează exact la fel.

Dacă avem mai mulți termeni? Nu e mare lucru.) Împărțim funcția în termeni și căutăm derivata fiecărui termen independent de ceilalți. De exemplu:

Aflați derivata funcției y=sinx - x 2 +cosx - x +3

Scriem cu curaj:

y" = (sinx)" - (x 2)" + (cosx)" - (x)" + (3)"

La sfârșitul lecției voi oferi sfaturi pentru a face viața mai ușoară atunci când diferențiez.)

Sfaturi practice:

1. Înainte de diferențiere, vedeți dacă este posibil să simplificați funcția inițială.

2. În exemple complicate, descriem soluția în detaliu, cu toate parantezele și liniuțele.

3. La diferențierea fracțiilor cu un număr constant la numitor, transformăm împărțirea în înmulțire și folosim regula 4.