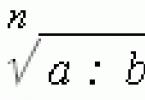
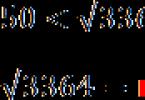Գործողություններ ուժերով և արմատներով: Աստիճան բացասականով ,

զրոյական և կոտորակային ցուցիչ։ Անիմաստ արտահայտությունների մասին.

Գործողություններ աստիճաններով.

1. Նույն հիմքով հզորությունները բազմապատկելիս գումարվում են դրանց ցուցիչները:

մի մ · a n = a m + n.

2. Նույն հիմքով աստիճաններ բաժանելիս՝ դրանց ցուցիչները հանել .

3. Երկու կամ ավելի գործակիցների արտադրյալի աստիճանը հավասար է այդ գործոնների աստիճանների արտադրյալին։

(աբգ… ) n = a n· b n · c n…

4. Հարաբերակցության (կոտորակի) աստիճանը հավասար է դիվիդենտի (համարիչ) և բաժանարարի (հայտարարի) աստիճանների հարաբերությանը.

(ա/բ ) n = a n / b n .

5. Աստիճանը հզորության բարձրացնելիս դրանց ցուցանիշները բազմապատկվում են.

(մի մ ) n = a m n .

Վերոնշյալ բոլոր բանաձևերը կարդացվում և կատարվում են երկու ուղղությամբ՝ ձախից աջ և հակառակը։

ՕՐԻՆԱԿ (2 · 3 · 5 / 15)² = 2² 3² 5² / 15² = 900 / 225 = 4 .

Գործողություններ արմատներով. Ստորև բերված բոլոր բանաձևերում խորհրդանիշը նշանակում է թվաբանական արմատ(արմատական ​​արտահայտությունը դրական է):

1. Մի քանի գործոնների արտադրյալի արմատը հավասար է արտադրյալին այս գործոնների արմատները.

2. Հարաբերակցության արմատը հավասար է շահաբաժնի և բաժանարարի արմատների հարաբերությանը.

3. Երբ արմատ բարձրացնելով իշխանության, բավական է բարձրացնել այս իշխանությունը արմատային համարը:

4. Եթե ​​բարձրացնենք արմատի աստիճանը ներսմ մեկ անգամ և միաժամանակ բարձրացնելմ րդ հզորությունը արմատային թիվ է, ապա արմատի արժեքը չի փոխվի.

5. Եթե ​​իջեցնենք արմատի աստիճանը ներսմ արդյունահանեք արմատը մեկ անգամ և միևնույն ժամանակմ րդ աստիճան արմատական ​​թվից, ապա արմատի արժեքը չէկփոխվի.

Աստիճանի հայեցակարգի ընդլայնում. Առայժմ աստիճաններ ենք դիտարկել միայն բնական ցուցանիշով.բայց գործողությունները աստիճաններն ու արմատները նույնպես կարող են հանգեցնել բացասական, զրոև կոտորակայինցուցանիշները։ Այս բոլոր ցուցանիշները պահանջում են լրացուցիչ սահմանում:

Բացասական ցուցիչով աստիճան: Որոշ թվի հզորությունը հետ բացասական (ամբողջական) ցուցանիշը սահմանվում է որպես միավոր, որը բաժանվում է բացարձակ արժեքին հավասար ցուցիչով նույն թվի ուժինբացասական ցուցանիշ.

Տայժմ բանաձեւ մի մ: a n= մի մ - n կարող է օգտագործվել ոչ միայնմ, ավելի քան n, այլեւ ժ մ, ավելի քիչ քան n .

ՕՐԻՆԱԿ ա 4 :ա 7 = ա 4 - 7 = ա - 3 .

Եթե ​​ուզում ենք բանաձեւըմի մ : a n= մի մ - nարդար էրm = n, մեզ անհրաժեշտ է զրոյական աստիճանի սահմանում:

Աստիճան զրոյական ցուցիչով: Զրո ցուցիչով ցանկացած ոչ զրոյական թվի աստիճանը 1 է:

ՕՐԻՆՆԵՐ. 2 0 = 1, ( – 5) 0 = 1, (– 3 / 5) 0 = 1.

Աստիճան կոտորակային ցուցիչով: Իրական թիվ բարձրացնելու համարև մինչև մ / ն հզորությունը , դուք պետք է հանեք արմատը n-րդ հզորությունը մ այս թվի հզորությունըա :

Անիմաստ արտահայտությունների մասին. Նման մի քանի արտահայտություններ կան.ցանկացած թիվ.

Իսկապես, եթե ենթադրենք, որ այս արտահայտությունը հավասար է ինչ-որ թվի x, ապա բաժանման գործողության սահմանման համաձայն ունենք՝ 0 = 0 x. Բայց այս հավասարությունը պահպանվում է ցանկացած x թիվ, որը պետք է ապացուցվեր։

Դեպք 3

0 0 - ցանկացած թիվ.

Իսկապես,

Լուծում Դիտարկենք երեք հիմնական դեպք.

1) x = 0 – այս արժեքը չի բավարարում այս հավասարմանը

(Ինչու՞):

2) երբ x> 0 մենք ստանում ենք. x / x = 1, այսինքն. 1 = 1, որտեղից հետևում է.

ինչ x- ցանկացած թիվ; բայց հաշվի առնելով դա

Մեր գործը x> 0, պատասխանն էx > 0 ;

3) երբ x < 0 получаем: – x / x= 1, այսինքն . –1 = 1, հետևաբար,

Այս դեպքում լուծում չկա։

Այս կերպ, x > 0.

Շատ հաճախ խնդիրներ լուծելիս բախվում ենք մեծ թվերի, որոնցից պետք է քաղել Քառակուսի արմատ. Շատ ուսանողներ որոշում են, որ դա սխալ է և սկսում են լուծել ամբողջ օրինակը: Ոչ մի դեպքում դա չպետք է արվի: Դրա համար երկու պատճառ կա.

1. Մեծ թվերի արմատները իսկապես առաջանում են խնդիրների մեջ: Հատկապես տեքստում;
2. Կա ալգորիթմ, որով այս արմատները դիտարկվում են գրեթե բանավոր:

Մենք այսօր կքննարկենք այս ալգորիթմը: Միգուցե որոշ բաներ ձեզ անհասկանալի թվան։ Բայց եթե ուշադրություն դարձնեք այս դասին, դուք կստանաք ամենահզոր զենքը դրա դեմ քառակուսի արմատներ.

Այսպիսով, ալգորիթմը.

1. Սահմանափակեք ցանկալի արմատը վերևում և ներքևում 10-ի բազմապատիկներով: Այսպիսով, մենք կնվազեցնենք որոնման տիրույթը մինչև 10 համար;
2. Այս 10 թվերից մաքրեք նրանց, որոնք հաստատ արմատներ չեն կարող լինել: Արդյունքում կմնա 1-2 թիվ;
3. Այս 1-2 թվերը քառակուսի դարձրեք: Դրանցից այն, որի քառակուսին հավասար է սկզբնական թվին, կլինի արմատը։

Մինչ այս ալգորիթմի գործնականում աշխատելը, եկեք նայենք յուրաքանչյուր առանձին քայլին:

Արմատների սահմանափակում

Նախևառաջ պետք է պարզել, թե որ թվերի միջև է գտնվում մեր արմատը։ Շատ ցանկալի է, որ թվերը լինեն տասի բազմապատիկ.

10 2 = 100;
20 2 = 400;
30 2 = 900;
40 2 = 1600;
...
90 2 = 8100;
100 2 = 10 000.

Մենք ստանում ենք թվերի շարք.

100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.

Ի՞նչ են մեզ տալիս այս թվերը: Պարզ է՝ մենք սահմաններ ենք ստանում: Վերցնենք, օրինակ, 1296 թիվը: Այն գտնվում է 900-ի և 1600-ի միջև: Հետևաբար, դրա արմատը չի կարող լինել 30-ից փոքր և 40-ից մեծ:

[Նկարի վերնագիր]

Նույնը ցանկացած այլ թվի դեպքում, որտեղից կարող եք գտնել քառակուսի արմատը: Օրինակ, 3364:

[Նկարի վերնագիր]

Այսպիսով, անհասկանալի թվի փոխարեն մենք ստանում ենք շատ կոնկրետ տիրույթ, որի մեջ ընկած է սկզբնական արմատը: Որոնման շրջանակն ավելի նեղացնելու համար անցեք երկրորդ քայլին:

Ակնհայտ ավելորդ թվերի վերացում

Այսպիսով, մենք ունենք 10 թիվ՝ արմատի թեկնածուներ։ Մենք դրանք շատ արագ ստացանք՝ առանց բարդ մտածելու ու սյունակում բազմապատկելու։ Շարժվելու ժամանակն է.

Հավատում եք, թե ոչ, հիմա մենք կնվազեցնենք թեկնածուների թիվը երկուսի, և կրկին առանց որևէ բարդ հաշվարկի: Բավական է իմանալ հատուկ կանոնը. Ահա այն:

Քառակուսու վերջին թվանշանը կախված է միայն վերջին թվանշանից բնօրինակ համարը.

Այլ կերպ ասած, բավական է նայել քառակուսու վերջին թվանշանին, և մենք անմիջապես կհասկանանք, թե որտեղ է ավարտվում սկզբնական թիվը։

Կան ընդամենը 10 թվանշան, որոնք կարող են լինել վերջին տեղում: Փորձենք պարզել, թե ինչի են դրանք վերածվում քառակուսու վրա։ Նայեք աղյուսակին.

1	2	3	4	5	6	7	8	9	0
1	4	9	6	5	6	9	4	1	0

Այս աղյուսակը ևս մեկ քայլ է արմատը հաշվարկելու համար: Ինչպես տեսնում եք, երկրորդ տողի թվերը հինգի նկատմամբ սիմետրիկ են ստացվել։ Օրինակ:

2 2 = 4;
8 2 = 64 → 4.

Ինչպես տեսնում եք, վերջին թվանշանը երկու դեպքում էլ նույնն է։ Իսկ դա նշանակում է, որ, օրինակ, 3364-ի արմատը անպայման ավարտվում է 2-ով կամ 8-ով: Մյուս կողմից, մենք հիշում ենք նախորդ պարբերության սահմանափակումը: Մենք ստանում ենք.

[Նկարի վերնագիր]

Կարմիր քառակուսիները ցույց են տալիս, որ մենք դեռ չգիտենք այս ցուցանիշը: Բայց ի վերջո, արմատը գտնվում է 50-ի և 60-ի միջև, որի վրա կան միայն երկու թվեր, որոնք ավարտվում են 2-ով և 8-ով.

[Նկարի վերնագիր]

Այսքանը: Բոլոր հնարավոր արմատներից մենք թողեցինք միայն երկու տարբերակ: Եվ սա ամենադժվար դեպքում է, քանի որ վերջին թվանշանը կարող է լինել 5 կամ 0: Եվ այդ դեպքում արմատների միակ թեկնածուն կմնա:

Վերջնական հաշվարկներ

Այսպիսով, մեզ մնացել է 2 թեկնածուական համար։ Ինչպե՞ս գիտես, թե որն է արմատը: Պատասխանն ակնհայտ է՝ երկու թվերի քառակուսի: Այն մեկը, որը քառակուսի է դնում, կտա սկզբնական թիվը և կլինի արմատը:

Օրինակ՝ 3364 թվի համար մենք գտանք երկու թեկնածու թիվ՝ 52 և 58։ Եկեք դրանք քառակուսի դարձնենք.

52 2 \u003d (50 +2) 2 \u003d 2500 + 2 50 2 + 4 \u003d 2704;
58 2 \u003d (60 - 2) 2 \u003d 3600 - 2 60 2 + 4 \u003d 3364:

Այսքանը: Պարզվեց, որ արմատը 58 է: Միաժամանակ, հաշվարկները պարզեցնելու համար օգտագործեցի գումարի և տարբերության քառակուսիների բանաձևը։ Դրա շնորհիվ դուք նույնիսկ ստիպված չեք եղել բազմապատկել թվերը սյունակում: Սա հաշվարկների օպտիմալացման ևս մեկ մակարդակ է, բայց, իհարկե, լրիվ ընտրովի է :)

Արմատային հաշվարկի օրինակներ

Տեսությունը լավն է, իհարկե։ Բայց եկեք փորձարկենք այն գործնականում:

[Նկարի վերնագիր]

Նախ, եկեք պարզենք, թե որ թվերի միջև է գտնվում 576 թիվը.

400 < 576 < 900
20 2 < 576 < 30 2

Հիմա նայենք վերջին թվին։ Այն հավասար է 6-ի: Ե՞րբ է դա տեղի ունենում: Միայն եթե արմատն ավարտվում է 4-ով կամ 6-ով: Ստանում ենք երկու թիվ.

Մնում է քառակուսի դնել յուրաքանչյուր թիվը և համեմատել բնօրինակի հետ.

24 2 = (20 + 4) 2 = 576

Գերազանց! Առաջին քառակուսին պարզվեց, որ հավասար է սկզբնական թվին։ Այսպիսով, սա է արմատը:

Առաջադրանք. Հաշվիր քառակուսի արմատը.

[Նկարի վերնագիր]

900 < 1369 < 1600;
30 2 < 1369 < 40 2;

Դիտարկենք վերջին թիվը.

1369 → 9;
33; 37.

Եկեք հրապարակենք այն.

33 2 \u003d (30 + 3) 2 \u003d 900 + 2 30 3 + 9 \u003d 1089 ≠ 1369;
37 2 \u003d (40 - 3) 2 \u003d 1600 - 2 40 3 + 9 \u003d 1369:

Ահա պատասխանը՝ 37.

Առաջադրանք. Հաշվիր քառակուսի արմատը.

[Նկարի վերնագիր]

Մենք սահմանափակում ենք թիվը.

2500 < 2704 < 3600;
50 2 < 2704 < 60 2;

Դիտարկենք վերջին թիվը.

2704 → 4;
52; 58.

Եկեք հրապարակենք այն.

52 2 = (50 + 2) 2 = 2500 + 2 50 2 + 4 = 2704;

Ստացանք պատասխանը՝ 52. Երկրորդ թիվն այլևս քառակուսի դնելու կարիք չի ունենա։

Առաջադրանք. Հաշվիր քառակուսի արմատը.

[Նկարի վերնագիր]

Մենք սահմանափակում ենք թիվը.

3600 < 4225 < 4900;
60 2 < 4225 < 70 2;

Դիտարկենք վերջին թիվը.

4225 → 5;
65.

Ինչպես տեսնում եք, երկրորդ քայլից հետո մնում է միայն մեկ տարբերակ՝ 65. Սա ցանկալի արմատն է։ Բայց եկեք այն դեռ քառակուսի դարձնենք և ստուգենք.

65 2 = (60 + 5) 2 = 3600 + 2 60 5 + 25 = 4225;

Ամեն ինչ ճիշտ է։ Գրում ենք պատասխանը.

Եզրակացություն

Ավաղ, ավելի լավ չէ: Եկեք նայենք պատճառներին: Դրանցից երկուսն են.

• Արգելվում է հաշվիչներ օգտագործել ցանկացած նորմալ մաթեմատիկայի քննության ժամանակ, լինի դա GIA, թե միասնական պետական ​​քննություն: Իսկ հաշվիչը դասարան տանելու համար նրանց հեշտությամբ կարող են դուրս հանել քննությունից:
• Մի նմանվեք հիմար ամերիկացիներին. Որոնք արմատների նման չեն. նրանք չեն կարող ավելացնել երկու պարզ թվեր: Իսկ ֆրակցիաներ տեսնելիս նրանք հիմնականում հիստերիայի մեջ են ընկնում։

Արտահայտության մեջ քառակուսի արմատների առկայությունը բարդացնում է բաժանման գործընթացը, սակայն կան կանոններ, որոնցով կոտորակների հետ աշխատանքը շատ ավելի հեշտ է դառնում։

Միակ բանը, որ պետք է մշտապես հիշել- արմատական ​​արտահայտությունները բաժանվում են արմատական ​​արտահայտությունների, իսկ գործոնները՝ գործոնների։ Քառակուսի արմատները բաժանելու գործընթացում մենք պարզեցնում ենք կոտորակը։ Նաև հիշեք, որ արմատը կարող է լինել հայտարարի մեջ:

Մեթոդ 1. Արմատական ​​արտահայտությունների բաժանում

Գործողությունների ալգորիթմ.

Գրի՛ր կոտորակ

Եթե ​​արտահայտությունը ներկայացված չէ որպես կոտորակ, ապա անհրաժեշտ է գրել այսպես, քանի որ ավելի հեշտ է հետևել քառակուսի արմատները բաժանելու սկզբունքին։

Օրինակ 1

144 ÷ 36 , այս արտահայտությունը պետք է վերաշարադրվի այսպես՝ 144 36

Օգտագործեք մեկ արմատային նշան

Եթե ​​և՛ համարիչը, և՛ հայտարարը պարունակում են քառակուսի արմատներ, ապա անհրաժեշտ է դրանց արմատային արտահայտությունները գրել նույն արմատային նշանի տակ՝ լուծման գործընթացը հեշտացնելու համար։

Հիշեցնում ենք, որ արմատական ​​արտահայտությունը (կամ թիվը) արտահայտություն է արմատային նշանի տակ։

Օրինակ 2

144 36 . Այս արտահայտությունը պետք է գրել այսպես՝ 144 36

Արմատային արտահայտությունների բաժանում

Պարզապես մի արտահայտությունը բաժանեք մյուսի և արդյունքը գրեք արմատի նշանի տակ:

Օրինակ 3

144 36 = 4 , այս արտահայտությունը գրում ենք հետևյալ կերպ՝ 144 36 = 4

Պարզեցնել արմատական ​​արտահայտությունը (անհրաժեշտության դեպքում)

Եթե ​​արմատային արտահայտությունը կամ գործոններից մեկը կատարյալ քառակուսի է, պարզեցրեք այդ արտահայտությունը:

Հիշեցնենք, որ կատարյալ քառակուսին այն թիվն է, որը ինչ-որ ամբողջ թվի քառակուսին է:

Օրինակ 4

4-ը կատարյալ քառակուսի է, քանի որ 2 × 2 = 4: Հետևաբար.

4 = 2 × 2 = 2: Հետեւաբար 144 36 = 4 = 2:

Մեթոդ 2. Արմատական ​​արտահայտության տարրալուծում գործոնների

Գործողությունների ալգորիթմ.

Գրի՛ր կոտորակ

Արտահայտությունը վերագրիր որպես կոտորակ (եթե այն ներկայացված է որպես այդպիսին): Սա մեծապես հեշտացնում է քառակուսի արմատներով արտահայտությունների բաժանման գործընթացը, հատկապես ֆակտորինգի ժամանակ։

Օրինակ 5

8 ÷ 36, վերագրեք այսպես 8 36

Գործոնավորե՛ք արմատական ​​արտահայտություններից յուրաքանչյուրը

Արմատի տակ գտնվող թիվը, ինչպես ցանկացած այլ ամբողջ թիվ, գործակիցները գրեք միայն արմատի նշանի տակ:

Օրինակ 6

8 36 = 2 x 2 x 2 6 x 6

Պարզեցնել կոտորակի համարիչն ու հայտարարը

Դրա համար անհրաժեշտ է արմատային նշանի տակից հանել գործակիցները, որոնք լրիվ քառակուսի են։ Այսպիսով, արմատային արտահայտության գործոնը դառնում է գործոն արմատային նշանից առաջ։

Օրինակ 7

2 2 6 6 × 6 2 × 2 × 2, որից հետևում է՝ 8 36 = 2 2 6

Ռացիոնալացնել հայտարարը (ազատվել արմատից)

Մաթեմատիկայի մեջ կան կանոններ, ըստ որոնց՝ արմատը հայտարարի մեջ թողնելը անճաշակության նշան է, այսինքն. դա արգելված է. Եթե ​​հայտարարի մեջ կա քառակուսի արմատ, ապա ազատվեք դրանից։

Բազմապատկեք համարիչն ու հայտարարը քառակուսի արմատով, որից ցանկանում եք ազատվել:

Օրինակ 8

6 2 3 արտահայտության մեջ դուք պետք է բազմապատկեք համարիչը և հայտարարը 3-ով, որպեսզի ձերբազատվեք հայտարարի մեջ.

6 2 3 × 3 3 = 6 2 × 3 3 × 3 = 6 6 9 = 6 6 3

Պարզեցրեք ստացված արտահայտությունը (անհրաժեշտության դեպքում)

Եթե ​​համարիչը և հայտարարը պարունակում են թվեր, որոնք կարող են և պետք է կրճատվեն: Պարզեցրո՛ւ այնպիսի արտահայտություններ, ինչպես ցանկացած կոտորակ:

Օրինակ 9

2 6 պարզեցնում է 1 3; այնպես որ 2 2 6-ը պարզեցնում է 1 2 3 = 2 3

Մեթոդ 3. Քառակուսի արմատների բաժանում գործակիցներով

Գործողությունների ալգորիթմ.

Պարզեցրեք բազմապատկիչները

Հիշեցնենք, որ գործոնները արմատային նշանի դիմաց թվերն են: Գործոնները պարզեցնելու համար անհրաժեշտ կլինի դրանք բաժանել կամ նվազեցնել: Մի դիպչեք արմատային արտահայտություններին:

Օրինակ 10

4 32 6 16 . Նախ, մենք կրճատում ենք 4 6. բաժանում ենք 2-ի և՛ համարիչը, և՛ հայտարարը՝ 4 6 \u003d 2 3:

Պարզեցնել քառակուսի արմատները

Եթե ​​համարիչը հավասարապես բաժանվում է հայտարարի վրա, ապա բաժանիր։ Եթե ​​ոչ, ապա պարզեցրեք արմատական ​​արտահայտությունները, ինչպես մյուսները:

Օրինակ 11

32-ը հավասարապես բաժանվում է 16-ի, ուստի՝ 32 16 = 2

Բազմապատկել պարզեցված գործոնները պարզեցված արմատներով

Հիշեք կանոնը. արմատները մի թողեք հայտարարի մեջ: Հետևաբար, մենք պարզապես համարիչն ու հայտարարը բազմապատկում ենք այս արմատով։

Օրինակ 12

2 3 × 2 = 2 2 3

Ռացիոնալացնել հայտարարը (ազատվել հայտարարի արմատից)

Օրինակ 13

4 3 2 7 . Բազմապատկեք համարիչը և հայտարարը 7-ով, որպեսզի ազատվեք հայտարարի արմատից:

4 3 7 × 7 7 = 4 3 × 7 7 × 7 = 4 21 49 = 4 21 7

Մեթոդ 4. Բաժանում քառակուսի արմատ ունեցող երկանդամով

Գործողությունների ալգորիթմ.

Որոշեք, թե արդյոք երկանդամը (երկանդամը) հայտարարի մեջ է

Հիշեցնենք, որ երկանդամը արտահայտություն է, որը ներառում է 2 միանդամ: Այս մեթոդը տեղի է ունենում միայն այն դեպքերում, երբ հայտարարը քառակուսի արմատ ունեցող երկանդամ է:

Օրինակ 14

1 5 + 2 - հայտարարում կա երկանդամ, քանի որ կան երկու միանդամներ:

Գտեք երկանդամին խոնարհված արտահայտությունը

Հիշեցնենք, որ խոնարհված երկանդամը երկանդամ է նույն միանդամներով, բայց հակադիր նշաններով: Արտահայտությունը պարզեցնելու և հայտարարի արմատից ազատվելու համար պետք է բազմապատկել խոնարհված երկանդամները։

Օրինակ 15

5 + 2 և 5 - 2-ը խոնարհված երկանդամներ են:

Բազմապատկեք համարիչն ու հայտարարը հայտարարի երկանդամին խոնարհված երկանդամով

Այս տարբերակը կօգնի ազատվել հայտարարի արմատից, քանի որ խոնարհված երկանդամների արտադրյալը հավասար է յուրաքանչյուր երկանդամ անդամի քառակուսիների տարբերությանը. (a - b) (a + b) = a 2 - b 2:

Օրինակ 16

1 5 + 2 = 1 (5 - 2) (5 - 2) (5 + 2) = 5 - 2 (5 2 - (2) 2 = 5 - 2 25 - 2 = 5 - 2 23 .

Սրանից հետևում է՝ 1 5 + 2 = 5 - 2 23։

Tips:

1. Եթե ​​դուք աշխատում եք խառը թվերի քառակուսի արմատներով, ապա դրանք դարձրեք ոչ պատշաճ կոտորակի:
2. Բաժանումից գումարման և հանման տարբերությունն այն է, որ բաժանման դեպքում արմատական ​​արտահայտությունները խորհուրդ չի տրվում պարզեցնել (լիարժեք քառակուսիների պատճառով):
3. Երբեք (!) մի թողեք արմատը հայտարարի մեջ:
4. Ոչ մի տասնորդական կամ արմատից առաջ խառնված. անհրաժեշտ է դրանք վերածել սովորական կոտորակի, այնուհետև պարզեցնել:
5. Հայտարարը երկու միանդամների գումարն է, թե տարբերությունը: Նման երկանդամը բազմապատկեք նրա խոնարհված երկանդամով և ազատվեք հայտարարի արմատից:

Եթե ​​տեքստում սխալ եք նկատել, ընդգծեք այն և սեղմեք Ctrl+Enter

Արմատը հանելու գործողությունը գործնականում հաջողությամբ օգտագործելու համար հարկավոր է ծանոթանալ այս գործողության հատկություններին։
Բոլոր հատկությունները ձևակերպված և ապացուցված են միայն արմատային նշանների տակ պարունակվող փոփոխականների ոչ բացասական արժեքների համար:

Թեորեմ 1. Երկու ոչ բացասական չիպսեթների արտադրյալի n-րդ արմատը (n=2, 3, 4,...) հավասար է այս թվերի n-րդ արմատների արտադրյալին.

Մեկնաբանություն:

1. Թեորեմ 1-ը մնում է վավեր այն դեպքում, երբ արմատական ​​արտահայտությունը երկուից ավելի ոչ բացասական թվերի արտադրյալ է։

Թեորեմ 2.Եթե, իսկ n-ը 1-ից մեծ բնական թիվ է, ապա հավասարությունը

Կարճ(թեև ոչ ճշգրիտ) ձևակերպում, որն ավելի հարմար է գործնականում օգտագործելու համար. կոտորակի արմատը հավասար է արմատների կոտորակին։

Թեորեմ 1-ը թույլ է տալիս մեզ բազմապատկել մ միայն նույն աստիճանի արմատներ , այսինքն. միայն նույն ցուցիչով արմատները:

Թեորեմ 3. Եթե ,k-ն բնական թիվ է, իսկ n-ը՝ 1-ից մեծ բնական թիվ, ապա հավասարությունը

Այսինքն՝ բնական ուժի վրա արմատ բարձրացնելու համար բավական է արմատական ​​արտահայտությունը բարձրացնել այս ուժի վրա։
Սա 1-ին թեորեմի հետևանքն է: Իսկապես, օրինակ, k = 3-ի համար մենք ստանում ենք

Թեորեմ 4. Եթե ,k, n-ը 1-ից մեծ բնական թվեր են, ապա հավասարությունը

Այսինքն՝ արմատից արմատ հանելու համար բավական է արմատների արտահայտիչները բազմապատկել։
Օրինակ,

Զգույշ եղիր!Մենք իմացանք, որ արմատների վրա կարելի է կատարել չորս գործողություն՝ բազմապատկում, բաժանում, հզորացում և արմատից հանում (արմատից): Իսկ ի՞նչ կասեք արմատների գումարման ու հանման մասին։ Ոչ մի դեպքում.
Օրինակ, դուք չեք կարող գրել Indeed-ի փոխարեն, բայց դա ակնհայտ է

Թեորեմ 5. Եթե արմատի և արմատային արտահայտության ցուցիչները բազմապատկվում կամ բաժանվում են նույն բնական թվով, ապա արմատի արժեքը չի փոխվի, այսինքն.

Խնդիրների լուծման օրինակներ

Օրինակ 1Հաշվիր

Լուծում.Օգտագործելով արմատների առաջին հատկությունը (թեորեմ 1), մենք ստանում ենք.

Օրինակ 2Հաշվիր
Լուծում.Խառը թիվը դարձրեք ոչ պատշաճ կոտորակի:
Մենք օգտագործում ենք արմատների երկրորդ հատկությունը ( թեորեմ 2 ), մենք ստանում ենք.

Օրինակ 3Հաշվարկել.

Լուծում.Հանրահաշվի ցանկացած բանաձև, ինչպես լավ գիտեք, օգտագործվում է ոչ միայն «ձախից աջ», այլ նաև «աջից ձախ»։ Այսպիսով, արմատների առաջին հատկությունը նշանակում է, որ այն կարող է ներկայացվել որպես և, ընդհակառակը, փոխարինվել արտահայտությամբ։ Նույնը վերաբերում է արմատների երկրորդ հատկությանը. Հաշվի առնելով սա՝ եկեք կատարենք հաշվարկները։

Շնորհավորում ենք. այսօր մենք կվերլուծենք արմատները՝ 8-րդ դասարանի ամենահուզիչ թեմաներից մեկը: :)

Շատերը շփոթվում են արմատների հետ կապված ոչ թե այն պատճառով, որ դրանք բարդ են (ինչը բարդ է՝ մի քանի սահմանում և ևս մի քանի հատկություն), այլ այն պատճառով, որ դպրոցական դասագրքերի մեծ մասում արմատները սահմանվում են այնպիսի վայրի ձևով, որ միայն դասագրքերի հեղինակներն իրենք կարող են։ հասկանալ այս խզբզոցը: Եվ նույնիսկ այն ժամանակ միայն մի շիշ լավ վիսկիով: :)

Հետևաբար, հիմա ես կտամ արմատի ամենաճիշտ և իրավասու սահմանումը. միակը, որը դուք իսկապես պետք է հիշեք: Եվ միայն այն ժամանակ ես կբացատրեմ՝ ինչու է այս ամենը անհրաժեշտ և ինչպես կիրառել այն գործնականում:

Բայց նախ հիշեք մի կարևոր կետ, որի մասին, չգիտես ինչու, դասագրքերի շատ կազմողներ «մոռանում են».

Արմատները կարող են լինել զույգ աստիճանի (մեր սիրելի $\sqrt(a)$, ինչպես նաև ցանկացած $\sqrt(a)$ և նույնիսկ $\sqrt(a)$) և կենտ աստիճանի (ցանկացած $\sqrt(a)$ , $\ sqrt(a)$ և այլն): Իսկ կենտ աստիճանի արմատի սահմանումը որոշակիորեն տարբերվում է զույգից։

Այստեղ այս «մի փոքր այլ կերպ» թաքնված է, հավանաբար, արմատների հետ կապված բոլոր սխալների և թյուրիմացությունների 95%-ը: Այսպիսով, եկեք մեկընդմիշտ պարզենք տերմինաբանությունը.

Սահմանում. Նույնիսկ արմատ n$a$ թվից ցանկացած է ոչ բացասական$b$ այնպիսի թիվ, որ $((b)^(n))=a$. Իսկ նույն $a$ թվից կենտ աստիճանի արմատը սովորաբար ցանկացած $b$ թիվ է, որի համար գործում է նույն հավասարությունը՝ $((b)^(n))=a$:

Ամեն դեպքում, արմատը նշվում է այսպես.

\(ա)\]

Նման նշումով $n$ թիվը կոչվում է արմատային ցուցիչ, իսկ $a$ թիվը կոչվում է արմատական ​​արտահայտություն: Մասնավորապես, $n=2$-ի համար մենք ստանում ենք մեր «սիրած» քառակուսի արմատը (ի դեպ, սա զույգ աստիճանի արմատ է), իսկ $n=3$-ի համար մենք ստանում ենք խորանարդ արմատ (կենտ աստիճան), որը հաճախ հանդիպում է նաև խնդիրների և հավասարումների մեջ։

Օրինակներ. Քառակուսի արմատների դասական օրինակներ.

\[\սկիզբ (հավասարեցնել) & \sqrt(4)=2; \\ & \sqrt(81)=9; \\ & \sqrt(256)=16. \\ \վերջ (հավասարեցնել)\]

Ի դեպ, $\sqrt(0)=0$ և $\sqrt(1)=1$: Սա միանգամայն տրամաբանական է, քանի որ $((0)^(2))=0$ և $((1)^(2))=1$:

Խորանարդ արմատները նույնպես տարածված են. մի վախեցեք դրանցից.

\[\սկիզբ (հավասարեցնել) & \sqrt(27)=3; \\ & \sqrt(-64)=-4; \\ & \sqrt(343)=7. \\ \վերջ (հավասարեցնել)\]

Դե, մի քանի «էկզոտիկ օրինակներ».

\[\սկիզբ (հավասարեցնել) & \sqrt(81)=3; \\ & \sqrt(-32)=-2. \\ \վերջ (հավասարեցնել)\]

Եթե ​​դուք չեք հասկանում, թե որն է տարբերությունը զույգ և կենտ աստիճանի միջև, նորից կարդացեք սահմանումը: Դա շատ կարեւոր է!

Միևնույն ժամանակ մենք կանդրադառնանք արմատների մեկ տհաճ հատկանիշին, որի պատճառով անհրաժեշտ էր առանձին սահմանում մտցնել զույգ և կենտ ցուցիչների համար:

Ինչու՞ մեզ ընդհանրապես արմատներ են պետք:

Սահմանումը կարդալուց հետո շատ ուսանողներ կհարցնեն. «Ի՞նչ էին ծխում մաթեմատիկոսները, երբ նրանք դա եկան»: Եվ իսկապես. ինչի՞ն են պետք այս բոլոր արմատները:

Այս հարցին պատասխանելու համար մի պահ վերադառնանք տարրական դպրոց։ Հիշեք՝ այն հեռավոր ժամանակներում, երբ ծառերն ավելի կանաչ էին, իսկ պելմեններն ավելի համեղ էին, մեր հիմնական մտահոգությունը թվերը ճիշտ բազմապատկելն էր։ Դե, ինչ-որ բան «հինգը հինգ - քսանհինգ» ոգով, այսքանը: Բայց ի վերջո, դուք կարող եք թվերը բազմապատկել ոչ թե զույգերով, այլ եռյակներով, չորսներով և ընդհանրապես ամբողջ բազմություններով.

\[\սկիզբ (հավասարեցնել) & 5\cdot 5=25; \\ & 5\cdot 5\cdot 5=125; \\ & 5\cdot 5\cdot 5\cdot 5=625; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5=3125; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5=15\ 625. \վերջ (հավասարեցնել)\]

Սակայն հարցը սա չէ։ Հնարքն այլ է՝ մաթեմատիկոսները ծույլ մարդիկ են, ուստի նրանք ստիպված են եղել գրի առնել տասը հինգի բազմապատկումը այսպես.

Այսպիսով, նրանք եկան աստիճաններ: Ինչու երկար տողի փոխարեն չգրել գործոնների թիվը որպես վերնագիր: Այս մեկի պես.

Շատ հարմար է! Բոլոր հաշվարկները կրճատվում են մի քանի անգամ, և դուք չեք կարող ծախսել նոթատետրերի մի փունջ մագաղաթյա թերթեր՝ գրի առնելու համար 5 183: Այդպիսի մուտքը կոչվում էր թվի աստիճան, նրա մեջ մի փունջ հատկություններ հայտնաբերվեցին, բայց երջանկությունը կարճատև ստացվեց։

Շքեղ խմիչքից հետո, որը կազմակերպվել էր հենց աստիճանների «հայտնաբերման» մասին, հատկապես քարկոծված մի մաթեմատիկոս հանկարծ հարցրեց. Իսկապես, եթե գիտենք, որ $b$ որոշակի թիվը, օրինակ, տալիս է 243 5-րդ աստիճանին, ապա ինչպե՞ս կարող ենք կռահել, թե ինքնին $b$ թիվը ինչի է հավասար։

Այս խնդիրը պարզվեց, որ շատ ավելի գլոբալ է, քան կարող էր թվալ առաջին հայացքից։ Որովհետև պարզվեց, որ «պատրաստի» աստիճանների մեծ մասի համար նման «նախնական» թվեր չկան։ Դատեք ինքներդ.

\[\սկիզբ(հավասարեցնել) & ((բ)^(3))=27\Աջ սլաք b=3\cdot 3\cdot 3\Rightarrow b=3; \\ & ((բ)^(3))=64\Աջ սլաք b=4\cdot 4\cdot 4\Rightarrow b=4. \\ \վերջ (հավասարեցնել)\]

Իսկ եթե $((b)^(3))=50$? Ստացվում է, որ պետք է գտնել որոշակի թիվ, որն իր վրա երեք անգամ բազմապատկելու դեպքում մեզ կտա 50։ Բայց ո՞րն է այս թիվը։ Այն ակնհայտորեն մեծ է 3-ից, քանի որ 3 3 = 27< 50. С тем же успехом оно меньше 4, поскольку 4 3 = 64 >50. Այսինքն. այս թիվը գտնվում է երեքից չորսի միջակայքում, բայց թե ինչի է այն հավասար, դուք կհասկանաք:

Հենց սա է պատճառը, որ մաթեմատիկոսները հայտնագործեցին $n$-րդ արմատները: Այդ իսկ պատճառով ներդրվեց $\sqrt(*)$ արմատական ​​պատկերակը։ Նշել նույն $b$ թիվը, որը նշված հզորությամբ մեզ կտա նախկինում հայտնի արժեք

\[\sqrt[n](a)=b\Աջ սլաք ((b)^(n))=a\]

Ես չեմ վիճում. հաճախ այդ արմատները հեշտությամբ են դիտարկվում. վերևում մենք տեսանք մի քանի նման օրինակ: Սակայն, այնուամենայնիվ, շատ դեպքերում, եթե դուք մտածում եք կամայական թվի մասին, ապա փորձում եք դրանից հանել կամայական աստիճանի արմատը, դուք դաժան աղետի մեջ եք:

Ի՞նչ կա այնտեղ։ Նույնիսկ ամենապարզ և ծանոթ $\sqrt(2)$-ը չի կարող ներկայացվել մեր սովորական ձևով` որպես ամբողջ թիվ կամ կոտորակ: Եվ եթե այս թիվը մտցնեք հաշվիչի մեջ, կտեսնեք սա.

\[\sqrt(2)=1.414213562...\]

Ինչպես տեսնում եք, տասնորդական կետից հետո գոյություն ունի թվերի անվերջ հաջորդականություն, որոնք չեն ենթարկվում ոչ մի տրամաբանության։ Դուք, իհարկե, կարող եք կլորացնել այս թիվը՝ այլ թվերի հետ արագ համեմատելու համար: Օրինակ:

\[\sqrt(2)=1.4142...\մոտ 1.4 \lt 1.5\]

Կամ ահա ևս մեկ օրինակ.

\[\sqrt(3)=1.73205...\մոտ 1.7 \gt 1.5\]

Բայց այս բոլոր կլորացումները, նախ, բավականին կոպիտ են. և երկրորդ, դուք նույնպես պետք է կարողանաք աշխատել մոտավոր արժեքներով, հակառակ դեպքում կարող եք բռնել ոչ ակնհայտ սխալների մի փունջ (ի դեպ, համեմատության և կլորացման հմտությունը պարտադիր կերպով ստուգվում է պրոֆիլի քննության ժամանակ):

Հետևաբար, լուրջ մաթեմատիկայի մեջ չի կարելի անել առանց արմատների. դրանք $\mathbb(R)$ բոլոր իրական թվերի բազմության նույն հավասար ներկայացուցիչներն են, ինչպես կոտորակներն ու ամբողջ թվերը, որոնք մենք վաղուց գիտենք:

Արմատը որպես $\frac(p)(q)$ ձևի կոտորակ ներկայացնելու անհնարինությունը նշանակում է, որ այս արմատը ռացիոնալ թիվ չէ։ Նման թվերը կոչվում են իռացիոնալ, և դրանք հնարավոր չէ ճշգրիտ ներկայացնել, բացառությամբ ռադիկալի կամ դրա համար հատուկ նախագծված այլ կառուցվածքների (լոգարիթմներ, աստիճաններ, սահմաններ և այլն) օգնությամբ։ Բայց դրա մասին ավելին մեկ այլ անգամ:

Դիտարկենք մի քանի օրինակ, որտեղ բոլոր հաշվարկներից հետո իռացիոնալ թվերը դեռ կմնան պատասխանում:

\[\begin(align) & \sqrt(2+\sqrt(27))=\sqrt(2+3)=\sqrt(5)\մոտ 2236... \\ & \sqrt(\sqrt(-32 ))=\sqrt(-2)\մոտ -12599... \\ \վերջ (հավասարեցնել)\]

Բնականաբար, արմատի տեսքով գրեթե անհնար է կռահել, թե որ թվերը կգան տասնորդական կետից հետո։ Այնուամենայնիվ, հնարավոր է հաշվարկել հաշվիչի վրա, բայց նույնիսկ ամենաառաջադեմ ամսաթվի հաշվիչը մեզ տալիս է իռացիոնալ թվի միայն առաջին մի քանի թվանշանները: Հետեւաբար, շատ ավելի ճիշտ է պատասխանները գրել $\sqrt(5)$ և $\sqrt(-2)$:

Հենց դրա համար են նրանք հորինվել։ Պատասխանները գրելը հեշտացնելու համար:

Ինչու են անհրաժեշտ երկու սահմանումներ:

Ուշադիր ընթերցողը հավանաբար արդեն նկատել է, որ օրինակներում բերված բոլոր քառակուսի արմատները վերցված են դրական թվերից։ Դե, գոնե զրոյից։ Բայց խորանարդի արմատները հանգիստ արդյունահանվում են բացարձակապես ցանկացած թվից՝ նույնիսկ դրական, նույնիսկ բացասական:

Ինչու է դա տեղի ունենում: Նայեք $y=((x)^(2))$ ֆունկցիայի գրաֆիկին:

Քառակուսային ֆունկցիայի գրաֆիկը տալիս է երկու արմատ՝ դրական և բացասական

Փորձենք այս գրաֆիկի միջոցով հաշվարկել $\sqrt(4)$: Դրա համար գրաֆիկի վրա գծված է $y=4$ հորիզոնական գիծ (նշված կարմիրով), որը հատում է պարաբոլը երկու կետում՝ $((x)_(1))=2$ և $((x) _(2)) =-2$: Սա միանգամայն տրամաբանական է, քանի որ

Առաջին թվով ամեն ինչ պարզ է, այն դրական է, հետևաբար այն արմատն է.

Բայց հետո ի՞նչ անել երկրորդ կետի հետ։ 4-ը միանգամից երկու արմատ ունի՞: Ի վերջո, եթե −2 թիվը քառակուսի տանենք, ապա կստանանք նաև 4։ Ինչո՞ւ չգրել $\sqrt(4)=-2$ այդ դեպքում։ Իսկ ինչո՞ւ են ուսուցիչները նման ձայնագրություններին նայում այնպես, կարծես ուզում են քեզ ուտել: :)

Խնդիրն այն է, որ եթե լրացուցիչ պայմաններ չառաջադրվեն, ապա չորսը կունենան երկու քառակուսի արմատ՝ դրական և բացասական: Եվ ցանկացած դրական թիվ կունենա նաև դրանցից երկուսը։ Բայց բացասական թվերն ընդհանրապես արմատներ չեն ունենա, դա երևում է նույն գրաֆիկից, քանի որ պարաբոլան երբեք չի ընկնում առանցքի տակ: y, այսինքն. չի ընդունում բացասական արժեքներ.

Նմանատիպ խնդիր առաջանում է բոլոր արմատների համար՝ զույգ ցուցիչով.

1. Խստորեն ասած՝ յուրաքանչյուր դրական թիվ կունենա երկու արմատ՝ $n$ զույգ ցուցիչով;
2. Բացասական թվերից նույնիսկ $n$-ով արմատն ընդհանրապես չի հանվում։

Դրա համար էլ $n$ զույգ արմատի սահմանումը հատուկ սահմանում է, որ պատասխանը պետք է լինի ոչ բացասական թիվ։ Ահա թե ինչպես ենք մենք ազատվում երկիմաստությունից.

Բայց կենտ $n$-ի դեպքում նման խնդիր չկա։ Սա տեսնելու համար եկեք նայենք $y=((x)^(3))$ ֆունկցիայի գրաֆիկին:

Խորանարդ պարաբոլան ընդունում է ցանկացած արժեք, ուստի խորանարդի արմատը կարելի է վերցնել ցանկացած թվից

Այս գրաֆիկից կարելի է երկու եզրակացություն անել.

1. Խորանարդ պարաբոլայի ճյուղերը, ի տարբերություն սովորականի, դեպի անսահմանություն են գնում երկու ուղղությամբ՝ և՛ վերև, և՛ վար: Հետևաբար, ինչ բարձրության վրա էլ հորիզոնական գիծ գծենք, այս գիծը անպայման հատվելու է մեր գրաֆիկի հետ։ Հետևաբար, խորանարդի արմատը միշտ կարելի է վերցնել, բացարձակապես ցանկացած թվից.
2. Բացի այդ, նման խաչմերուկը միշտ կլինի եզակի, այնպես որ դուք կարիք չունեք մտածելու, թե որ թիվը համարել «ճիշտ» արմատը, և որը վաստակել: Այդ իսկ պատճառով կենտ աստիճանի համար արմատների սահմանումն ավելի պարզ է, քան զույգի համար (ոչ բացասականության պահանջ չկա)։

Ափսոս, որ այս պարզ բաները չեն բացատրվում դասագրքերի մեծ մասում։ Փոխարենը, մեր ուղեղը սկսում է ճախրել բոլոր տեսակի թվաբանական արմատներով և դրանց հատկություններով:

Այո, ես չեմ վիճում, թե ինչ է թվաբանական արմատը, դուք նույնպես պետք է իմանաք: Եվ այս մասին մանրամասն կխոսեմ առանձին դասում։ Այսօր մենք կխոսենք նաև դրա մասին, քանի որ առանց դրա, $n$-th բազմակիության արմատների վերաբերյալ բոլոր մտորումները թերի կլինեն:

Բայց նախ դուք պետք է հստակ հասկանաք այն սահմանումը, որը ես տվեցի վերևում: Հակառակ դեպքում, տերմինների առատության պատճառով ձեր գլխում այնպիսի խառնաշփոթ կսկսվի, որ վերջում ընդհանրապես ոչինչ չեք հասկանա։

Եվ այն ամենը, ինչ դուք պետք է հասկանաք, զույգ և կենտ թվերի տարբերությունն է: Հետևաբար, ևս մեկ անգամ մենք կհավաքենք այն ամենը, ինչ դուք իսկապես պետք է իմանաք արմատների մասին.

1. Զույգ արմատը գոյություն ունի միայն ոչ բացասական թվից և ինքնին միշտ ոչ բացասական թիվ է: Բացասական թվերի համար նման արմատը որոշված ​​չէ:
2. Բայց կենտ աստիճանի արմատը գոյություն ունի ցանկացած թվից և ինքնին կարող է լինել ցանկացած թիվ. դրական թվերի համար այն դրական է, իսկ բացասական թվերի համար, ինչպես գլխարկն է հուշում, այն բացասական է:

Դժվա՞ր է։ Ոչ, դա դժվար չէ: Մաքրե՞լ: Այո, դա ակնհայտ է! Հետևաբար, հիմա մենք մի փոքր կվարժվենք հաշվարկներով։

Հիմնական հատկություններ և սահմանափակումներ

Արմատները շատ տարօրինակ հատկություններ և սահմանափակումներ ունեն, սա առանձին դաս կլինի: Հետևաբար, այժմ մենք կքննարկենք միայն ամենակարևոր «չիպը», որը վերաբերում է միայն հավասարաչափ արտահայտիչ ունեցող արմատներին: Մենք գրում ենք այս հատկությունը բանաձևի տեսքով.

\[\sqrt(((x)^(2n)))=\ձախ| x\աջ|\]

Այլ կերպ ասած, եթե թիվը բարձրացնենք մինչև զույգ հզորության, ապա դրանից հանենք նույն աստիճանի արմատը, ապա կստանանք ոչ թե սկզբնական թիվը, այլ դրա մոդուլը։ Սա պարզ թեորեմ է, որը հեշտ է ապացուցել (բավական է առանձին դիտարկել ոչ բացասական $x$, իսկ հետո առանձին դիտարկել բացասականները): Ուսուցիչները անընդհատ խոսում են այդ մասին, դա տրված է յուրաքանչյուր դպրոցական դասագրքում։ Բայց հենց որ բանը հասնում է իռացիոնալ հավասարումների (այսինքն՝ արմատականի նշան պարունակող հավասարումների) լուծմանը, ուսանողները միասին մոռանում են այս բանաձևը։

Խնդիրը մանրամասն հասկանալու համար եկեք մեկ րոպե մոռանանք բոլոր բանաձևերը և փորձենք հաշվել առաջ երկու թիվ.

\[\sqrt(((3)^(4)))=?\quad \sqrt(((\left(-3 \աջ))^(4)))=?\]

Սրանք շատ պարզ օրինակներ են։ Առաջին օրինակը կլուծի մարդկանց մեծ մասը, բայց երկրորդի վրա շատերը կպչում են։ Ցանկացած նման անհեթեթություն առանց խնդիրների լուծելու համար միշտ հաշվի առեք ընթացակարգը.

1. Նախ՝ թիվը հասցվում է չորրորդ իշխանության։ Դե, դա մի տեսակ հեշտ է: Կստացվի նոր թիվ, որը նույնիսկ կարելի է գտնել բազմապատկման աղյուսակում.
2. Եվ հիմա այս նոր թվից անհրաժեշտ է հանել չորրորդ աստիճանի արմատը։ Նրանք. արմատների և աստիճանների «կրճատում» չկա, դրանք հաջորդական գործողություններ են:

Եկեք զբաղվենք առաջին արտահայտությամբ՝ $\sqrt(((3)^(4)))$: Ակնհայտ է, որ նախ պետք է հաշվարկել արտահայտությունը արմատի տակ.

\[((3)^(4))=3\cdot 3\cdot 3\cdot 3=81\]

Այնուհետև մենք հանում ենք 81 թվի չորրորդ արմատը.

Հիմա նույնն անենք երկրորդ արտահայտության հետ։ Նախ, մենք −3 թիվը բարձրացնում ենք չորրորդ աստիճանի, որի համար անհրաժեշտ է այն ինքն իրենով 4 անգամ բազմապատկել.

\[((\left(-3 \աջ))^(4))=\left(-3 \աջ)\cdot \left(-3 \աջ)\cdot \left(-3 \աջ)\cdot \ ձախ (-3 \աջ)=81\]

Մենք ստացանք դրական թիվ, քանի որ արտադրանքի մինուսների ընդհանուր թիվը 4 հատ է, և դրանք բոլորը կչեղարկեն միմյանց (ի վերջո, մինուս մինուսը տալիս է գումարած): Հաջորդը, նորից հանեք արմատը.

Սկզբունքորեն, այս տողը չէր կարող գրվել, քանի որ անհեթեթ է, որ պատասխանը նույնն է լինելու: Նրանք. Նույն հավասար հզորության հավասար արմատը «այրում է» մինուսները, և այս առումով արդյունքը չի տարբերվում սովորական մոդուլից.

\[\սկիզբ(հավասարեցնել) & \sqrt((3)^(4)))=\ձախ| 3\աջ|=3; \\ & \sqrt(((\left(-3 \աջ))^(4)))=\ձախ| -3 \ճիշտ|=3. \\ \վերջ (հավասարեցնել)\]

Այս հաշվարկները լավ համընկնում են զույգ աստիճանի արմատի սահմանման հետ. արդյունքը միշտ ոչ բացասական է, իսկ արմատական ​​նշանը նույնպես միշտ ոչ բացասական թիվ է։ Հակառակ դեպքում, արմատը սահմանված չէ:

Նշում գործողությունների հերթականության վերաբերյալ

1. $\sqrt(((a)^(2)))$ նշումը նշանակում է, որ սկզբում քառակուսի ենք դնում $a$ թիվը, իսկ հետո վերցնում ստացված արժեքի քառակուսի արմատը։ Հետևաբար, մենք կարող ենք վստահ լինել, որ ոչ բացասական թիվը միշտ նստում է արմատային նշանի տակ, քանի որ $((a)^(2))\ge 0$ ամեն դեպքում;
2. Բայց $((\left(\sqrt(a) \right))^(2))$ նշումը, ընդհակառակը, նշանակում է, որ սկզբում մենք արմատը հանում ենք $a$ որոշակի թվից և հետո միայն արդյունքը քառակուսի ենք տալիս։ Հետևաբար, $a$ թիվը ոչ մի դեպքում չի կարող բացասական լինել. սա պարտադիր պահանջ է, որը ներառված է սահմանման մեջ:

Այսպիսով, ոչ մի դեպքում չի կարելի անմտորեն նվազեցնել արմատներն ու աստիճանները՝ դրանով իսկ իբր «պարզեցնելով» սկզբնական արտահայտությունը։ Որովհետև եթե արմատի տակ բացասական թիվ լինի, և դրա ցուցանիշը զույգ լինի, մենք շատ խնդիրներ կունենանք։

Սակայն այս բոլոր խնդիրները արդիական են միայն նույնիսկ ցուցանիշների համար։

Արմատային նշանի տակից հանելով մինուս նշանը

Բնականաբար, կենտ ցուցիչներով արմատները նույնպես ունեն իրենց առանձնահատկությունը, որը, սկզբունքորեն, գոյություն չունի զույգերի համար։ Այսինքն:

\[\sqrt(-a)=-\sqrt(a)\]

Մի խոսքով, կենտ աստիճանի արմատների նշանի տակից կարելի է մինուս հանել։ Սա շատ օգտակար հատկություն է, որը թույլ է տալիս «դուրս նետել» բոլոր մինուսները.

\[\սկիզբ(հավասարեցնել) & \sqrt(-8)=-\sqrt(8)=-2; \\ & \sqrt(-27)\cdot \sqrt(-32)=-\sqrt(27)\cdot \left(-\sqrt(32) \աջ)= \\ & =\sqrt(27)\cdot \sqrt(32)= \\ & =3\cdot 2=6. \վերջ (հավասարեցնել)\]

Այս պարզ հատկությունը մեծապես հեշտացնում է բազմաթիվ հաշվարկներ: Հիմա ձեզ պետք չէ անհանգստանալ. իսկ եթե բացասական արտահայտություն ընկնի արմատի տակ, և արմատի աստիճանը հավասար լինի: Բավական է «դուրս գցել» բոլոր մինուսները արմատներից դուրս, որից հետո դրանք կարելի է բազմապատկել միմյանցով, բաժանել և ընդհանրապես շատ կասկածելի բաներ անել, որոնք «դասական» արմատների դեպքում երաշխավորված են մեզ սխալի տանելու։ .

Եվ այստեղ ասպարեզ է մտնում մեկ այլ սահմանում՝ հենց այն, որով դպրոցներից շատերը սկսում են իռացիոնալ արտահայտությունների ուսումնասիրությունը: Եվ առանց որի մեր հիմնավորումը թերի կլիներ։ Հանդիպե՛ք

թվաբանական արմատ

Մի պահ ենթադրենք, որ արմատային նշանի տակ կարող են լինել միայն դրական թվերը կամ ծայրահեղ դեպքում՝ զրոն։ Եկեք միավորներ հավաքենք զույգ / կենտ ցուցանիշների վրա, գնահատենք վերը նշված բոլոր սահմանումները. մենք կաշխատենք միայն ոչ բացասական թվերով: Ուրեմն ինչ?

Եվ հետո մենք ստանում ենք թվաբանական արմատը՝ այն մասամբ հատվում է մեր «ստանդարտ» սահմանումների հետ, բայց դեռ տարբերվում է դրանցից։

Սահմանում. Ոչ բացասական $a$ թվի $n$th աստիճանի թվաբանական արմատը ոչ բացասական $b$ թիվ է, որ $((b)^(n))=a$:

Ինչպես տեսնում եք, մեզ այլևս չի հետաքրքրում պարիտետը։ Փոխարենը հայտնվեց նոր սահմանափակում՝ արմատական ​​արտահայտությունն այժմ միշտ ոչ բացասական է, իսկ արմատն ինքնին նույնպես ոչ բացասական է։

Ավելի լավ հասկանալու համար, թե ինչպես է թվաբանական արմատը տարբերվում սովորականից, նայեք մեզ արդեն ծանոթ քառակուսի և խորանարդ պարաբոլայի գրաֆիկներին.

Արմատային որոնման տարածք - ոչ բացասական թվեր

Ինչպես տեսնում եք, այսուհետ մեզ հետաքրքրում են միայն գրաֆիկների այն կտորները, որոնք գտնվում են առաջին կոորդինատային եռամսյակում, որտեղ $x$ և $y$ կոորդինատները դրական են (կամ առնվազն զրո): Այլևս կարիք չկա ցուցիչին նայել՝ հասկանալու համար՝ մենք իրավունք ունե՞նք բացասական թիվ արմատավորելու, թե՞ ոչ։ Քանի որ բացասական թվերն այլեւս սկզբունքորեն չեն դիտարկվում։

Դուք կարող եք հարցնել. «Դե, ինչի՞ն է մեզ պետք այդքան ամորձատված սահմանումը»: Կամ. «Ինչու՞ մենք չենք կարողանում հաղթահարել վերը նշված ստանդարտ սահմանումը»:

Դե, ես կտամ ընդամենը մեկ հատկություն, որի պատճառով նոր սահմանումը տեղին է դառնում։ Օրինակ՝ էքսպոենտացիայի կանոնը.

\[\sqrt[n](a)=\sqrt(((a)^(k)))\]

Խնդրում ենք նկատի ունենալ. մենք կարող ենք արմատական ​​արտահայտությունը բարձրացնել ցանկացած հզորության և միևնույն ժամանակ բազմապատկել արմատային ցուցիչը նույն հզորությամբ, և արդյունքը կլինի նույն թիվը: Ահա մի քանի օրինակներ.

\[\սկիզբ(հավասարեցնել) & \sqrt(5)=\sqrt(((5)^(2)))=\sqrt(25) \\ & \sqrt(2)=\sqrt(((2)^ (4)))=\sqrt(16) \\ \վերջ (հավասարեցնել)\]

Լավ, ի՞նչ վատ բան կա դրա մեջ։ Ինչո՞ւ նախկինում չէինք կարող դա անել: Ահա թե ինչու. Դիտարկենք մի պարզ արտահայտություն. $\sqrt(-2)$-ը մեր դասական իմաստով միանգամայն նորմալ, բայց թվաբանական արմատի տեսանկյունից բացարձակապես անընդունելի թիվ է։ Փորձենք փոխակերպել այն.

$\begin(align) & \sqrt(-2)=-\sqrt(2)=-\sqrt(((2)^(2)))=-\sqrt(4) \lt 0; \\ & \sqrt(-2)=\sqrt(((\left(-2 \աջ))^(2)))=\sqrt(4) \gt 0. \\ \վերջ (հավասարեցնել)$

Ինչպես տեսնում եք, առաջին դեպքում մինուսը հանեցինք ռադիկալի տակից (մենք լրիվ իրավունք ունենք, քանի որ ցուցանիշը կենտ է), իսկ երկրորդում՝ վերը նշված բանաձևը։ Նրանք. մաթեմատիկայի տեսանկյունից ամեն ինչ արվում է ըստ կանոնների։

WTF?! Ինչպե՞ս կարող է նույն թիվը լինել և՛ դրական, և՛ բացասական: Ոչ մի դեպքում. Պարզապես դրական թվերի և զրոյի դեպքում հզորացման բանաձևը սկսում է լրիվ հերետիկոսություն տալ բացասական թվերի դեպքում։

Այստեղ նման երկիմաստությունից ազատվելու համար թվաբանական արմատներ են հորինել։ Առանձին մեծ դաս է նվիրված նրանց, որտեղ մենք մանրամասնորեն դիտարկում ենք նրանց բոլոր հատկությունները: Այսպիսով, հիմա մենք դրանց վրա չենք անդրադառնա, ամեն դեպքում դասը չափազանց երկար ստացվեց:

Հանրահաշվական արմատ. նրանց համար, ովքեր ցանկանում են ավելին իմանալ

Երկար մտածեցի՝ այս թեման առանձին պարբերությամբ դարձնել, թե ոչ։ Ի վերջո որոշեցի հեռանալ այստեղից։ Այս նյութը նախատեսված է նրանց համար, ովքեր ցանկանում են ավելի լավ հասկանալ արմատները՝ այլևս ոչ թե միջին «դպրոցական» մակարդակով, այլ օլիմպիադային մոտ մակարդակով:

Այսպիսով, բացի $n$-րդ աստիճանի արմատի «դասական» սահմանումից և հարակից բաժանումից զույգ և կենտ ցուցանիշների, կա ավելի «մեծահասակ» սահմանում, որը կախված չէ հավասարությունից և ընդհանրապես այլ նրբություններ: Սա կոչվում է հանրահաշվական արմատ:

Սահմանում. Ցանկացած $a$-ի հանրահաշվական $n$-th արմատը $b$ բոլոր թվերի բազմությունն է, որպեսզի $((b)^(n))=a$: Նման արմատների համար լավ հաստատված նշանակում չկա, ուստի վերևում պարզապես գծիկ դրեք.

\[\ overline(\sqrt[n](a))=\left\(b\left| b\in \mathbb(R);((b)^(n))=a \աջ. \աջ\) \]

Դասի սկզբում տրված ստանդարտ սահմանումից հիմնարար տարբերությունն այն է, որ հանրահաշվական արմատը կոնկրետ թիվ չէ, այլ բազմություն: Եվ քանի որ մենք աշխատում ենք իրական թվերի հետ, այս հավաքածուն ընդամենը երեք տեսակի է.

1. Դատարկ հավաքածու։ Առաջանում է, երբ բացասական թվից պահանջվում է գտնել զույգ աստիճանի հանրահաշվական արմատ.
2. Հավաքածու, որը բաղկացած է մեկ տարրից: Այս կատեգորիային են պատկանում կենտ հզորությունների բոլոր արմատները, ինչպես նաև զրոյից զույգ հզորությունների արմատները.
3. Վերջապես, հավաքածուն կարող է ներառել երկու թիվ՝ նույն $((x)_(1))$ և $((x)_(2))=-((x)_(1))$, որոնք մենք տեսանք աղյուսակ քառակուսի ֆունկցիա: Համապատասխանաբար, նման հավասարեցում հնարավոր է միայն դրական թվից զույգ աստիճանի արմատը հանելիս։

Վերջին դեպքն ավելի մանրամասն քննարկման է արժանի։ Տարբերությունը հասկանալու համար եկեք հաշվենք մի քանի օրինակ։

Օրինակ. Հաշվարկել արտահայտությունները.

\[\overline(\sqrt(4));\quad \overline(\sqrt(-27));\quad \overline(\sqrt(-16)).\]

Լուծում. Առաջին արտահայտությունը պարզ է.

\[\ overline (\sqrt(4))=\ձախ\( 2;-2 \աջ\)\]

Դա երկու թվեր են, որոնք կազմում են հավաքածուի մի մասը: Որովհետև դրանցից յուրաքանչյուրը քառակուսի վրա տալիս է չորս:

\[\overline(\sqrt(-27))=\ձախ\( -3 \աջ\)\]

Այստեղ մենք տեսնում ենք մի շարք, որը բաղկացած է միայն մեկ թվից: Սա միանգամայն տրամաբանական է, քանի որ արմատի ցուցիչը կենտ է:

Վերջապես, վերջին արտահայտությունը.

\[\overline(\sqrt(-16))=\varnothing \]

Մենք ստացանք դատարկ հավաքածու: Որովհետև չկա մեկ իրական թիվ, որը չորրորդ (այսինքն՝ զույգ) հզորության բարձրանալիս մեզ բացասական −16 թիվ տա։

Վերջնական նշում. Խնդրում եմ նկատի ունեցեք, պատահական չէ, որ ես ամենուր նշել եմ, որ մենք աշխատում ենք իրական թվերով։ Որովհետև կան նաև կոմպլեքս թվեր - այնտեղ $\sqrt(-16)$ և շատ այլ տարօրինակ բաներ կարելի է հաշվել։

Այնուամենայնիվ, մաթեմատիկայի ժամանակակից դպրոցական ծրագրում բարդ թվեր գրեթե երբեք չեն գտնվել: Դրանք դասագրքերի մեծ մասից դուրս են մնացել, քանի որ մեր պաշտոնյաները թեման համարում են «չափազանց դժվար հասկանալի»։

Այսքանը: Հաջորդ դասում մենք կդիտարկենք արմատների բոլոր հիմնական հատկությունները և վերջապես կսովորենք, թե ինչպես պարզեցնել իռացիոնալ արտահայտությունները: :)