3.1. Polarne koordinate

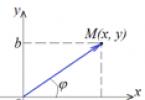
Često se koristi u avionu polarni koordinatni sustav . Definirano je ako je zadana točka O tzv pol, i zraka koja izlazi iz pola (za nas je ovo os Ox) je polarna os. Položaj točke M je fiksiran s dva broja: polumjer (ili radijus vektor) i kut φ između polarne osi i vektora . Kut φ naziva se polarni kut; mjereno u radijanima i računajući u smjeru suprotnom od kazaljke na satu od polarne osi.

Položaj točke u polarnom koordinatnom sustavu zadan je uređenim parom brojeva (r; φ). Na polu r = 0 a φ nije definiran. Za sve ostale točke r > 0 a φ je definiran do višekratnika 2π. U tom slučaju parovima brojeva (r; φ) i (r 1 ; φ 1) pridružuje se ista točka ako je .

Za pravokutni koordinatni sustav xOy Kartezijeve koordinate točke lako se izražavaju u smislu njezinih polarnih koordinata na sljedeći način:

3.2. Geometrijska interpretacija kompleksnog broja

Promotrimo na ravnini Kartezijev pravokutni koordinatni sustav xOy.

Svakom kompleksnom broju z=(a, b) pridružuje se točka ravnine s koordinatama ( x, y), Gdje koordinata x = a, tj. realni dio kompleksnog broja, a koordinata y = bi imaginarni dio.

Ravnina čije su točke kompleksni brojevi je kompleksna ravnina.

Na slici kompleksni broj z = (a, b) meč lopta M(x, y).

Vježbajte.Nacrtaj kompleksne brojeve na koordinatnoj ravnini:

3.3. Trigonometrijski oblik kompleksnog broja

Kompleksni broj u ravnini ima koordinate točke M(x; y). pri čemu:

Zapisivanje kompleksnog broja - trigonometrijski oblik kompleksnog broja.

Broj r se zove modul složeni broj z i označava se. Modul je nenegativan realan broj. Za .

Modul je nula ako i samo ako z = 0, tj. a=b=0.

Broj φ naziva se argument z i označeno. Argument z definiran je višeznačno, poput polarnog kuta u polarnom koordinatnom sustavu, naime do višekratnika 2π.

Tada prihvaćamo: , gdje je φ najmanja vrijednost argumenta. Očito je da

.

Uz dublje proučavanje teme, uvodi se pomoćni argument φ*, tako da

Primjer 1. Pronađite trigonometrijski oblik kompleksnog broja.

Riješenje. 1) razmatramo modul: ;

2) traženje φ: ;

3) trigonometrijski oblik:

Primjer 2 Pronađite algebarski oblik kompleksnog broja .

Ovdje je dovoljno zamijeniti vrijednosti trigonometrijskih funkcija i transformirati izraz:

Primjer 3 Naći modul i argument kompleksnog broja;

1) ;

2) ; φ - u 4 četvrtine:

3.4. Operacije s kompleksnim brojevima u trigonometrijskom obliku

· Zbrajanje i oduzimanje prikladnije je izvoditi s kompleksnim brojevima u algebarskom obliku:

· Množenje– uz pomoć jednostavnih trigonometrijskih transformacija može se pokazati da kod množenja moduli brojeva se množe, a argumenti se dodaju: ;

Predavanje

Trigonometrijski oblik kompleksnog broja

Plan

1.Geometrijski prikaz kompleksnih brojeva.

2.Trigonometrijski zapis kompleksnih brojeva.

3. Djelovanje na kompleksne brojeve u trigonometrijskom obliku.

Geometrijski prikaz kompleksnih brojeva.

a) Kompleksni brojevi se prikazuju točkama ravnine prema sljedećem pravilu: a + dvo = M ( a ; b ) (Sl. 1).

Slika 1

b) Kompleksni broj može se prikazati kao vektor koji počinje u točkiOKO a završavaju u zadanoj točki (slika 2).

Slika 2

Primjer 7. Nacrtajte točke koje predstavljaju kompleksne brojeve:1; - ja ; - 1 + ja ; 2 – 3 ja (slika 3).

Slika 3

Trigonometrijski zapis kompleksnih brojeva.

Složeni brojz = a + dvo može se postaviti pomoću radijus - vektora s koordinatama( a ; b ) (slika 4).

Slika 4

Definicija . Duljina vektora predstavlja kompleksni brojz , nazivamo modulom tog broja i označavamo ilir .

Za bilo koji kompleksni brojz njegov modulr = | z | se jednoznačno određuje formulom .

Definicija . Vrijednost kuta između pozitivnog smjera realne osi i vektora koji predstavlja kompleksan broj naziva se argument ovog kompleksnog broja i označava seA rg z iliφ .

Argument kompleksnog brojaz = 0 neodređeno. Argument kompleksnog brojaz≠ 0 je višeznačna veličina i određena je do člana2πk (k = 0; - 1; 1; - 2; 2; ...): Arg z = arg z + 2πk , Gdjearg z - glavna vrijednost argumenta, zatvorena u intervalu(-π; π] , to je-π < arg z ≤ π (ponekad se vrijednost koja pripada intervalu uzima kao glavna vrijednost argumenta .

Ova formula zar =1 često se naziva De Moivreova formula:

(cos φ + i sin φ) n = cos (nφ) + i sin (nφ), n  N .

Primjer 11 Izračunaj(1 + ja ) 100 .

Napišimo kompleksan broj1 + ja u trigonometrijskom obliku.

a = 1, b = 1 .

cos φ = , sin φ = , φ = .

(1+i) 100 = [ (cos + griješim )] 100 = ( ) 100 (cos 100 + ja griješim 100) = = 2 50 (cos 25π + i sin 25π) = 2 50 (cos π + i sin π) = - 2 50 .

4) Vađenje kvadratnog korijena kompleksnog broja.

Prilikom vađenja kvadratnog korijena kompleksnog brojaa + dvo imamo dva slučaja:

Akob > oko , To ;

2.3. Trigonometrijski oblik kompleksnih brojeva

Neka je vektor zadan na kompleksnoj ravnini brojem .

Označimo s φ kut između pozitivne poluosi Ox i vektora (kut φ se smatra pozitivnim ako se računa suprotno od kazaljke na satu, a negativnim u protivnom).

Duljinu vektora označimo s r. Zatim . Također označavamo

Zapisivanje kompleksnog broja različitog od nule z kao

naziva se trigonometrijski oblik kompleksnog broja z. Broj r nazivamo modulom kompleksnog broja z, a broj φ argumentom tog kompleksnog broja i označavamo ga s Arg z.

Trigonometrijski oblik zapisa kompleksnog broja - (Eulerova formula) - eksponencijalni oblik zapisa kompleksnog broja:

Kompleksni broj z ima beskonačno mnogo argumenata: ako je φ0 bilo koji argument broja z, tada se svi ostali mogu pronaći po formuli

Za kompleksni broj argument i trigonometrijski oblik nisu definirani.

Dakle, argument kompleksnog broja različitog od nule je bilo koje rješenje sustava jednadžbi:

(3)

Vrijednost φ argumenta kompleksnog broja z koji zadovoljava nejednakosti naziva se glavna vrijednost i označava se s arg z.

Argumenti Arg z i arg z međusobno su povezani jednakošću

, (4)

Formula (5) je posljedica sustava (3), pa svi argumenti kompleksnog broja zadovoljavaju jednakost (5), ali nisu sva rješenja φ jednadžbe (5) argumenti broja z.

Glavna vrijednost argumenta kompleksnog broja različitog od nule nalazi se pomoću formula:

Formule za množenje i dijeljenje kompleksnih brojeva u trigonometrijskom obliku su sljedeće:

. (7)

Kod podizanja kompleksnog broja na prirodni potenciju koristi se de Moivreova formula:

Pri izvlačenju korijena iz kompleksnog broja koristi se formula:

, (9)

gdje je k=0, 1, 2, …, n-1.

Zadatak 54. Izračunajte , gdje je .

Rješenje ovog izraza predstavimo u eksponencijalnom obliku zapisa kompleksnog broja: .

Ako tada .

zatim, . Stoga, dakle I , Gdje .

Odgovor: , u .

Zadatak 55. Napiši kompleksne brojeve u trigonometrijskom obliku:

A) ; b) ; V) ; G) ; e) ; e) ; i) .

Budući da je trigonometrijski oblik kompleksnog broja , tada je:

a) U složenom broju: .

,

Zato

b) , Gdje ,

G) , Gdje ,

e) .

i) , A , To .

Zato

Odgovor: ; 4; ; ; ; ; .

Zadatak 56. Odredite trigonometrijski oblik kompleksnog broja

.

Neka, .

zatim, , .

Jer i , , zatim , i

Stoga, dakle

Odgovor: , Gdje .

Zadatak 57. Koristeći trigonometrijski oblik kompleksnog broja izvršite sljedeće radnje: .

Zamislite brojeve i u trigonometrijskom obliku.

1), gdje Zatim

Pronalaženje vrijednosti glavnog argumenta:

Zamijenite vrijednosti i u izraz , dobivamo

2) gdje onda

Zatim

3) Nađi kvocijent

Uz pretpostavku k=0, 1, 2, dobivamo tri različite vrijednosti željenog korijena:

Ako tada

ako tada

ako tada .

Odgovor: :

:

: .

Zadatak 58. Neka su , , , različiti kompleksni brojevi i . Dokaži to

broj je realan pozitivan broj;

b) jednakost se odvija:

a) Predstavimo ove kompleksne brojeve u trigonometrijskom obliku:

jer .

Hajdemo to pretvarati. Zatim

.

Posljednji izraz je pozitivan broj, jer se ispod predznaka sinusa nalaze brojevi iz intervala.

jer broj stvarno i pozitivno. Doista, ako su a i b kompleksni brojevi i realni su i veći od nule, tada je .

Osim,

dakle tražena jednakost je dokazana.

Zadatak 59. Zapiši broj u algebarskom obliku .

Broj predstavljamo u trigonometrijskom obliku, a zatim nalazimo njegov algebarski oblik. Imamo . Za dobivamo sustav:

Iz ovoga slijedi jednakost: .

Primjenom De Moivreove formule:

dobivamo

Nađen je trigonometrijski oblik zadanog broja.

Sada zapisujemo ovaj broj u algebarskom obliku:

.

Odgovor: .

Zadatak 60. Odredite zbroj , ,

Razmotrite zbroj

Primjenom De Moivreove formule nalazimo

Ovaj zbroj je zbroj n članova geometrijske progresije s nazivnikom i prvi član .

Primjenom formule za zbroj članova takve progresije imamo

Odvajanjem imaginarnog dijela u posljednjem izrazu nalazimo

Odvajanjem realnog dijela dobivamo i sljedeću formulu: , , .

Zadatak 61. Nađi zbroj:

A) ; b) .

Prema Newtonovoj formuli za dizanje na potenciju, imamo

Prema De Moivreovoj formuli nalazimo:

Izjednačavanjem realnog i imaginarnog dijela dobivenih izraza za imamo:

I .

Ove formule se mogu napisati u kompaktnom obliku na sljedeći način:

,

, gdje je cijeli dio broja a.

Zadatak 62. Pronađite sve za koje .

Jer , zatim primjenom formule

, Za vađenje korijena, dobivamo ,

Stoga, , ,

, .

Točke koje odgovaraju brojevima nalaze se na vrhovima kvadrata upisanog u krug polumjera 2 sa središtem u točki (0;0) (slika 30).

Odgovor: , ,

, .

Zadatak 63. Riješite jednadžbu , .

Po stanju ; dakle, ova jednadžba nema korijen, i, prema tome, ona je ekvivalentna jednadžbi.

Da bi broj z bio korijen ove jednadžbe, broj mora biti n-ti korijen broja 1.

Stoga zaključujemo da izvorna jednadžba ima korijene određene iz jednakosti

,

Tako,

,

tj. ,

Odgovor: .

Zadatak 64. Riješite jednadžbu u skupu kompleksnih brojeva.

Budući da broj nije korijen ove jednadžbe, tada je ova jednadžba ekvivalentna jednadžbi

Odnosno jednadžba.

Svi korijeni ove jednadžbe dobivaju se iz formule (vidi problem 62):

; ; ; ; .

Zadatak 65. Na kompleksnoj ravnini nacrtati skup točaka koje zadovoljavaju nejednakosti: . (2. način rješavanja problema 45)

Neka .

Kompleksni brojevi s istim modulima odgovaraju točkama ravnine koje leže na kružnici sa središtem u ishodištu, pa nejednakost zadovoljavaju sve točke otvorenog prstena omeđenog kružnicama sa zajedničkim središtem u ishodištu i polumjerima i (slika 31). Neka neka točka kompleksne ravnine odgovara broju w0. Broj , ima modul puta manji od modula w0, argument koji je veći od argumenta w0. S geometrijskog gledišta, točka koja odgovara w1 može se dobiti korištenjem homotetije sa središtem u ishodištu i koeficijenta, kao i rotacijom u smjeru suprotnom od kazaljke na satu u odnosu na ishodište. Kao rezultat primjene ove dvije transformacije na točke prstena (slika 31), potonji će se pretvoriti u prsten omeđen kružnicama s istim središtem i polumjerima 1 i 2 (slika 32).

transformacija implementira se pomoću paralelne translacije na vektoru. Prenoseći prsten sa središtem u točki na naznačeni vektor, dobivamo prsten iste veličine sa središtem u točki (slika 22).

Predložena metoda, koja koristi ideju geometrijskih transformacija ravnine, vjerojatno je manje prikladna u opisu, ali je vrlo elegantna i učinkovita.

Zadatak 66. Nađi ako .

Neka , zatim i . Izvorna jednakost poprimit će oblik . Iz uvjeta jednakosti dvaju kompleksnih brojeva dobivamo , , odakle , . Tako, .

Zapišimo broj z u trigonometrijskom obliku:

, Gdje , . Prema De Moivreovoj formuli nalazimo .

Odgovor: - 64.

Zadatak 67. Za kompleksan broj pronađite sve kompleksne brojeve tako da je , i .

Predstavimo broj u trigonometrijskom obliku:

. Stoga , . Za broj koji dobijemo, može biti jednak bilo kojem.

U prvom slučaju , u drugom

.

Odgovor: , .

Zadatak 68. Nađi zbroj brojeva tako da je . Navedite jedan od ovih brojeva.

Napominjemo da se već iz same formulacije problema može shvatiti da se zbroj korijena jednadžbe može pronaći bez izračunavanja samih korijena. Doista, zbroj korijena jednadžbe je koeficijent od , uzet sa suprotnim predznakom (općeniti Vieta teorem), tj.

Učenici, školska dokumentacija, donose zaključke o stupnju asimilacije ovog pojma. Sažeti proučavanje značajki matematičkog mišljenja i procesa formiranja pojma kompleksnog broja. Opis metoda. Dijagnostika: I stadij. Razgovor je obavljen s učiteljicom matematike koja predaje algebru i geometriju u 10. razredu. Razgovor je nastao nakon što je proteklo neko vrijeme...

Rezonancija" (!)), koja uključuje i procjenu vlastitog ponašanja. 4. Kritičku procjenu vlastitog razumijevanja situacije (sumnje). 5. Na kraju, korištenje preporuka pravne psihologije (uzimanje u obzir psiholoških aspekata profesionalne radnje koje obavlja odvjetnik - profesionalna psihološka pripremljenost) Razmotrimo sada psihološku analizu pravnih činjenica. ...

Matematika trigonometrijske supstitucije i provjera učinkovitosti razvijene metodike nastave. Faze rada: 1. Izrada izbornog predmeta na temu: „Primjena trigonometrijske supstitucije za rješavanje algebarskih problema“ s učenicima u razredima s produbljenim učenjem matematike. 2. Izvođenje razvijenog izbornog predmeta. 3. Provođenje dijagnostičke kontrole...

Spoznajni zadaci služe samo kao dopuna postojećim nastavnim sredstvima i trebaju biti u odgovarajućoj kombinaciji sa svim tradicionalnim sredstvima i elementima odgojno-obrazovnog procesa. Razlika obrazovnih problema u nastavi humanističkih znanosti od egzaktnih, matematičkih problema je samo u tome što u povijesnim problemima nema formula, krutih algoritama i sl., što otežava njihovo rješavanje. ...

KOMPLEKSNI BROJEVI XI

§ 256. Trigonometrijski oblik kompleksnih brojeva

Neka kompleksni broj a + bi odgovara vektoru OA> s koordinatama ( a, b ) (vidi sliku 332).

Duljinu ovog vektora označimo sa r , i kut koji čini s osi x , kroz φ . Po definiciji sinusa i kosinusa:

a / r = cos φ , b / r = grijeh φ .

Zato A = r cos φ , b = r grijeh φ . Ali u ovom slučaju složeni broj a + bi može se napisati kao:

a + bi = r cos φ + ir grijeh φ = r (cos φ + ja grijeh φ ).

Kao što znate, kvadrat duljine bilo kojeg vektora jednak je zbroju kvadrata njegovih koordinata. Zato r 2 = a 2 + b 2, odakle r = √a 2 + b 2

Tako, bilo koji kompleksni broj a + bi može se predstaviti kao :

a + bi = r (cos φ + ja grijeh φ ), (1)

gdje je r = √a 2 + b 2 , i kut φ određuje se iz uvjeta:

Ovaj oblik zapisivanja složenih brojeva naziva se trigonometrijski.

Broj r u formuli (1) naziva se modul, i kut φ - argument, kompleksni broj a + bi .

Ako je kompleksan broj a + bi nije jednak nuli, tada je njegov modul pozitivan; ako a + bi = 0, tada a = b = 0 i tada r = 0.

Modul svakog kompleksnog broja jednoznačno je određen.

Ako je kompleksan broj a + bi nije jednak nuli, tada je njegov argument određen formulama (2) definitivno do kuta višekratnika 2 π . Ako a + bi = 0, tada a = b = 0. U ovom slučaju r = 0. Iz formule (1) lako je shvatiti da kao argument φ u ovom slučaju možete odabrati bilo koji kut: uostalom, za bilo koji φ

0 (cos φ + ja grijeh φ ) = 0.

Stoga nulti argument nije definiran.

Modul kompleksnog broja r ponekad označavaju | z |, a argument arg z . Pogledajmo nekoliko primjera prikaza kompleksnih brojeva u trigonometrijskom obliku.

Primjer. 1. 1 + ja .

Pronađimo modul r i argument φ ovaj broj.

r = √ 1 2 + 1 2 = √ 2 .

Stoga grijeh φ = 1 / √ 2 , cos φ = 1 / √ 2 , odakle φ = π / 4 + 2nπ .

Tako,

1 + ja = √ 2 ,

Gdje P - bilo koji cijeli broj. Obično se iz beskonačnog skupa vrijednosti argumenta kompleksnog broja izabere jedna koja je između 0 i 2 π . U ovom slučaju, ova vrijednost je π / 4 . Zato

1 + ja = √ 2 (cos π / 4 + ja grijeh π / 4)

Primjer 2 Napiši u trigonometrijskom obliku kompleksan broj √ 3 - ja . Imamo:

r = √ 3+1 = 2 cos φ = √ 3 / 2 , sin φ = - 1 / 2

Dakle, do kuta djeljivog s 2 π , φ = 11 / 6 π ; stoga,

√ 3 - ja = 2 (cos 11 / 6 π + ja grijeh 11/6 π ).

Primjer 3 Napiši u trigonometrijskom obliku kompleksan broj ja

složeni broj ja odgovara vektoru OA> završava u točki A osi na s ordinatom 1 (slika 333). Duljina takvog vektora jednaka je 1, a kut koji zatvara s osi apscisa jednak je π / 2. Zato

ja = cos π / 2 + ja grijeh π / 2 .

Primjer 4 Napiši kompleksni broj 3 u trigonometrijskom obliku.

Kompleksni broj 3 odgovara vektoru OA > x apscisa 3 (sl. 334).

Duljina takvog vektora je 3, a kut koji zatvara s osi x je 0. Prema tome

3 = 3 (cos 0 + ja grijeh 0),

Primjer 5 Napiši u trigonometrijskom obliku kompleksni broj -5.

Kompleksni broj -5 odgovara vektoru OA> završava u točki osi x s apscisom -5 (slika 335). Duljina takvog vektora je 5, a kut koji zatvara s osi x je π . Zato

5 = 5 (cos π + ja grijeh π ).

Vježbe

2047. Napiši ove kompleksne brojeve u trigonometrijskom obliku, definirajući njihove module i argumente:

1) 2 + 2√3 ja , 4) 12ja - 5; 7).3ja ;

2) √3 + ja ; 5) 25; 8) -2ja ;

3) 6 - 6ja ; 6) - 4; 9) 3ja - 4.

2048. Označite na ravnini skupove točaka koje predstavljaju kompleksne brojeve čiji moduli r i argumenti φ zadovoljavaju uvjete:

1) r = 1, φ = π / 4 ; 4) r < 3; 7) 0 < φ < π / 6 ;

2) r =2; 5) 2 < r <3; 8) 0 < φ < я;

3) r < 3; 6) φ = π / 3 ; 9) 1 < r < 2,

10) 0 < φ < π / 2 .

2049. Mogu li brojevi ujedno biti i moduli kompleksnog broja? r i - r ?

2050. Mogu li argument kompleksnog broja ujedno biti i kutovi φ i - φ ?

Predstavite ove kompleksne brojeve u trigonometrijskom obliku definiranjem njihovih modula i argumenata:

2051*. 1 + cos α + ja grijeh α . 2054*. 2 (cos 20° - ja grijeh 20°).

2052*. grijeh φ + ja cos φ . 2055*. 3(- cos 15° - ja grijeh 15°).