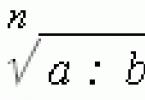
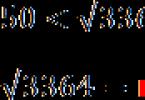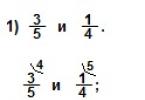अक्सर, समस्याओं को हल करते समय, हमें बड़ी संख्या का सामना करना पड़ता है जिससे हमें निकालने की आवश्यकता होती है वर्गमूल. कई छात्र यह तय करते हैं कि यह एक गलती है और पूरे उदाहरण को हल करना शुरू कर देते हैं। किसी भी हालत में ऐसा नहीं करना चाहिए! इसके दो कारण हैं:

1. बड़ी संख्या की जड़ें समस्याओं में होती हैं। विशेष रूप से पाठ में;
2. एक एल्गोरिथ्म है जिसके द्वारा इन जड़ों को लगभग मौखिक रूप से माना जाता है।

हम आज इस एल्गोरिथम पर विचार करेंगे। शायद कुछ बातें आपको समझ से बाहर लगेंगी। लेकिन अगर आप इस पाठ पर ध्यान देंगे तो आपको सबसे शक्तिशाली हथियार मिल जाएगा वर्गमूल.

तो एल्गोरिदम:

1. वांछित रूट को ऊपर और नीचे 10 के गुणकों तक सीमित करें। इस प्रकार, हम खोज सीमा को 10 संख्याओं तक कम कर देंगे;
2. इन 10 नंबरों में से उन्हें निकाल दें जो निश्चित रूप से रूट नहीं हो सकते हैं। नतीजतन, 1-2 नंबर रहेंगे;
3. इन 1-2 नंबरों का वर्ग करें। उनमें से वह, जिसका वर्ग मूल संख्या के बराबर है, मूल होगा।

इस एल्गोरिथम को व्यवहार में लागू करने से पहले, आइए प्रत्येक व्यक्तिगत चरण को देखें।

जड़ बाधा

सबसे पहले, हमें यह पता लगाने की आवश्यकता है कि हमारी जड़ किन संख्याओं के बीच स्थित है। यह अत्यधिक वांछनीय है कि संख्याएँ दस की गुणज हों:

10 2 = 100;
20 2 = 400;
30 2 = 900;
40 2 = 1600;
...
90 2 = 8100;
100 2 = 10 000.

हमें संख्याओं की एक श्रृंखला मिलती है:

100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.

ये संख्याएँ हमें क्या देती हैं? यह सरल है: हमें सीमाएँ मिलती हैं। उदाहरण के लिए, संख्या 1296 लें। यह 900 और 1600 के बीच स्थित है। इसलिए, इसकी जड़ 30 से कम और 40 से अधिक नहीं हो सकती:

[आंकड़ा अनुशीर्षक]

यही बात किसी अन्य संख्या के साथ भी है जिससे आप वर्गमूल निकाल सकते हैं। उदाहरण के लिए, 3364:

[आंकड़ा अनुशीर्षक]

इस प्रकार, एक अबोधगम्य संख्या के बजाय, हमें एक बहुत विशिष्ट श्रेणी मिलती है जिसमें मूल मूल स्थित होता है। खोज के दायरे को और कम करने के लिए, दूसरे चरण पर जाएँ।

स्पष्ट रूप से अनावश्यक संख्याओं का उन्मूलन

तो, हमारे पास 10 नंबर हैं - रूट के लिए उम्मीदवार। हमने उन्हें बहुत जल्दी प्राप्त किया, बिना जटिल सोच और एक कॉलम में गुणा किए। आगे चलने का समय आ गया है।

मानो या न मानो, अब हम उम्मीदवारों की संख्या घटाकर दो कर देंगे - और फिर बिना किसी जटिल गणना के! विशेष नियम जानना ही पर्याप्त है। यह रहा:

वर्ग का अंतिम अंक केवल अंतिम अंक पर निर्भर करता है मूल संख्या.

दूसरे शब्दों में, यह वर्ग के अंतिम अंक को देखने के लिए पर्याप्त है - और हम तुरंत समझ जाएंगे कि मूल संख्या कहाँ समाप्त होती है।

केवल 10 अंक हैं जो अंतिम स्थान पर हो सकते हैं। आइए यह पता लगाने की कोशिश करें कि जब वे चुकता किए जाते हैं तो वे क्या बन जाते हैं। तालिका पर एक नज़र डालें:

1	2	3	4	5	6	7	8	9	0
1	4	9	6	5	6	9	4	1	0

यह तालिका रूट की गणना करने की दिशा में एक और कदम है। जैसा कि आप देख सकते हैं, दूसरी पंक्ति में संख्याएँ पाँच के संबंध में सममित निकलीं। उदाहरण के लिए:

2 2 = 4;
8 2 = 64 → 4.

जैसा कि आप देख सकते हैं, अंतिम अंक दोनों मामलों में समान है। और इसका मतलब यह है कि, उदाहरण के लिए, 3364 की जड़ आवश्यक रूप से 2 या 8 में समाप्त होती है। दूसरी ओर, हम पिछले पैराग्राफ से प्रतिबंध को याद करते हैं। हम पाते हैं:

[आंकड़ा अनुशीर्षक]

लाल वर्ग दिखाते हैं कि हम अभी तक इस आंकड़े को नहीं जानते हैं। लेकिन आखिरकार, रूट 50 और 60 के बीच होता है, जिस पर 2 और 8 में समाप्त होने वाली केवल दो संख्याएँ होती हैं:

[आंकड़ा अनुशीर्षक]

बस इतना ही! सभी संभावित जड़ों में से, हमने केवल दो विकल्प छोड़े! और यह सबसे कठिन मामले में है, क्योंकि अंतिम अंक 5 या 0. हो सकता है और फिर जड़ों के लिए एकमात्र उम्मीदवार रह जाएगा!

अंतिम गणना

तो, हमारे पास 2 उम्मीदवारों की संख्या बची है। आप कैसे जानते हैं कि कौन सी जड़ है? उत्तर स्पष्ट है: दोनों संख्याओं का वर्ग करें। जो वर्ग करेगा वह मूल संख्या देगा, और वह मूल होगा।

उदाहरण के लिए, संख्या 3364 के लिए, हमें दो उम्मीदवार संख्याएँ मिलीं: 52 और 58।

52 2 \u003d (50 +2) 2 \u003d 2500 + 2 50 2 + 4 \u003d 2704;
58 2 \u003d (60 - 2) 2 \u003d 3600 - 2 60 2 + 4 \u003d 3364।

बस इतना ही! यह पता चला कि मूल 58 है! उसी समय, गणनाओं को सरल बनाने के लिए, मैंने योग और अंतर के वर्गों के सूत्र का उपयोग किया। इसके लिए धन्यवाद, आपको किसी कॉलम में संख्याओं को गुणा करने की भी आवश्यकता नहीं थी! यह गणनाओं के अनुकूलन का एक और स्तर है, लेकिन, निश्चित रूप से, यह पूरी तरह से वैकल्पिक है :)

रूट गणना उदाहरण

सिद्धांत अच्छा है, बिल्कुल। लेकिन आइए इसे व्यवहार में परखें।

[आंकड़ा अनुशीर्षक]

सबसे पहले, आइए जानें कि संख्या 576 किन संख्याओं के बीच स्थित है:

400 < 576 < 900
20 2 < 576 < 30 2

अब अंतिम संख्या को देखते हैं। यह 6 के बराबर है। ऐसा कब होता है? केवल अगर मूल 4 या 6 पर समाप्त होता है। हमें दो संख्याएँ मिलती हैं:

यह प्रत्येक संख्या को वर्गित करने और मूल के साथ तुलना करने के लिए बनी हुई है:

24 2 = (20 + 4) 2 = 576

उत्कृष्ट! पहला वर्ग मूल संख्या के बराबर निकला। तो यह जड़ है।

एक कार्य। वर्गमूल की गणना करें:

[आंकड़ा अनुशीर्षक]

900 < 1369 < 1600;
30 2 < 1369 < 40 2;

आइए अंतिम संख्या देखें:

1369 → 9;
33; 37.

आइए इसे स्क्वायर करें:

33 2 \u003d (30 + 3) 2 \u003d 900 + 2 30 3 + 9 \u003d 1089 ≠ 1369;
37 2 \u003d (40 - 3) 2 \u003d 1600 - 2 40 3 + 9 \u003d 1369।

यहाँ उत्तर है: 37।

एक कार्य। वर्गमूल की गणना करें:

[आंकड़ा अनुशीर्षक]

हम संख्या को सीमित करते हैं:

2500 < 2704 < 3600;
50 2 < 2704 < 60 2;

आइए अंतिम संख्या देखें:

2704 → 4;
52; 58.

आइए इसे स्क्वायर करें:

52 2 = (50 + 2) 2 = 2500 + 2 50 2 + 4 = 2704;

हमें उत्तर मिला: 52। दूसरी संख्या को अब चुकता करने की आवश्यकता नहीं होगी।

एक कार्य। वर्गमूल की गणना करें:

[आंकड़ा अनुशीर्षक]

हम संख्या को सीमित करते हैं:

3600 < 4225 < 4900;
60 2 < 4225 < 70 2;

आइए अंतिम संख्या देखें:

4225 → 5;
65.

जैसा कि आप देख सकते हैं, दूसरे चरण के बाद, केवल एक विकल्प रहता है: 65। यह वांछित जड़ है। लेकिन आइए फिर भी इसे चौकोर करें और जांचें:

65 2 = (60 + 5) 2 = 3600 + 2 60 5 + 25 = 4225;

सबकुछ सही है। हम उत्तर लिखते हैं।

निष्कर्ष

काश, कोई बेहतर नहीं। आइए कारणों पर एक नजर डालते हैं। उनमें से दो:

• किसी भी सामान्य गणित परीक्षा में कैलकुलेटर का उपयोग करना प्रतिबंधित है, चाहे वह GIA हो या एकीकृत राज्य परीक्षा। और कक्षा में कैलकुलेटर ले जाने के लिए उन्हें आसानी से परीक्षा से बाहर किया जा सकता है।
• मूर्ख अमेरिकियों की तरह मत बनो। जो मूल की तरह नहीं हैं - वे दो अभाज्य संख्याओं को नहीं जोड़ सकते हैं। और अंशों को देखते ही वे आम तौर पर हिस्टीरिकल हो जाते हैं।

शक्तियों और जड़ों के साथ संचालन। नकारात्मक के साथ डिग्री ,

शून्य और आंशिक सूचक। उन भावों के बारे में जिनका कोई मतलब नहीं है।

डिग्री के साथ संचालन।

1. समान आधार वाली शक्तियों को गुणा करने पर उनके संकेतक जुड़ जाते हैं:

पूर्वाह्न · एक एन = ए एम + एन।

2. एक ही आधार के साथ डिग्री को विभाजित करते समय, उनके संकेतक घटाया .

3. दो या दो से अधिक कारकों के उत्पाद की डिग्री इन कारकों की डिग्री के उत्पाद के बराबर होती है।

(एबीसी… ) एन = एक एन· बी एन · सी एन…

4. अनुपात (अंश) की डिग्री लाभांश (अंश) और भाजक (भाजक) की डिग्री के अनुपात के बराबर है:

(क/ख ) एन = ए एन / बी एन।

5. एक डिग्री को एक शक्ति तक बढ़ाते समय, उनके संकेतक गुणा किए जाते हैं:

(पूर्वाह्न ) एन = ए एम एन।

उपरोक्त सभी सूत्र बाएं से दाएं और इसके विपरीत दोनों दिशाओं में पढ़े और क्रियान्वित किए जाते हैं।

उदाहरण (2 · 3 · 5/15)² = 2² 3² 5² / 15² = 900 / 225 = 4 .

जड़ों के साथ संचालन। नीचे दिए गए सभी सूत्रों में, प्रतीक साधन अंकगणितीय जड़(कट्टरपंथी अभिव्यक्ति सकारात्मक है)।

1. कई कारकों के उत्पाद की जड़ उत्पाद के बराबर है इन कारकों की जड़ें:

2. अनुपात की जड़ भाज्य और भाजक की जड़ों के अनुपात के बराबर है:

3. जब एक जड़ को एक शक्ति के रूप में ऊपर उठाया जाता है, तो यह इस शक्ति को बढ़ाने के लिए पर्याप्त होता है जड़ संख्या:

4. अगर हम जड़ की डिग्री में वृद्धि करते हैंएम एक बार और एक साथ बढ़ाएँएम वें घात एक मूल संख्या है, तो मूल का मान नहीं बदलेगा:

5. यदि हम जड़ की डिग्री को कम करते हैंएम जड़ को एक बार और एक ही समय में निकालेंएम करणी संख्या से th घात है, तो मूल का मान नहीं हैबदल जाएगा:

डिग्री की अवधारणा का विस्तार। अब तक, हमने केवल एक प्राकृतिक संकेतक के साथ डिग्री पर विचार किया है;लेकिन कार्रवाई डिग्री और जड़ें भी ले जा सकती हैं नकारात्मक, शून्यतथा आंशिकसंकेतक। इन सभी घातांकों को एक अतिरिक्त परिभाषा की आवश्यकता है।

एक नकारात्मक प्रतिपादक के साथ डिग्री। के साथ कुछ संख्या की शक्ति नकारात्मक (संपूर्ण) सूचक को एक इकाई द्वारा विभाजित के रूप में परिभाषित किया गया है निरपेक्ष मान के बराबर एक्सपोनेंट के साथ समान संख्या की शक्ति के लिएनकारात्मक संकेतक:

टीअब सूत्र पूर्वाह्न: एक= पूर्वाह्न - एन के लिए ही नहीं इस्तेमाल किया जा सकता हैएम, इससे अधिक एन, लेकिन यह भी एम, से कम एन .

उदाहरण एक 4 :एक 7 = ए 4 - 7 = ए - 3 .

अगर हम सूत्र चाहते हैंपूर्वाह्न : एक= पूर्वाह्न - एनपर उचित थाएम = एन, हमें डिग्री शून्य की परिभाषा चाहिए।

शून्य प्रतिपादक के साथ डिग्री। शून्य घातांक वाली किसी भी अशून्य संख्या की घात 1 होती है।

उदाहरण। 2 0 = 1, ( – 5) 0 = 1, (– 3 / 5) 0 = 1.

भिन्नात्मक प्रतिपादक के साथ एक डिग्री। वास्तविक संख्या बढ़ाने के लिएऔर शक्ति एम / एन के लिए , आपको जड़ निकालने की जरूरत है m में से nवीं शक्ति इस संख्या की वें शक्तिएक :

उन भावों के बारे में जिनका कोई मतलब नहीं है। ऐसे कई भाव हैं।कोई संख्या।

दरअसल, अगर हम मान लें कि यह व्यंजक किसी संख्या के बराबर है एक्स, तो हमारे पास डिवीजन ऑपरेशन की परिभाषा के अनुसार: 0 = 0 एक्स. लेकिन यह समानता कायम है कोई संख्या एक्सजिसे साबित करना था।

मामला 3

0 0 - कोई संख्या।

सचमुच,

समाधान तीन मुख्य मामलों पर विचार करें:

1) एक्स = 0 – यह मान इस समीकरण को संतुष्ट नहीं करता है

(क्यों?)।

2) कब एक्स> 0 हमें मिलता है: एक्स / एक्स = 1, यानी 1 = 1, जहां से आता है,

क्या एक्स- कोई संख्या; लेकिन इसे ध्यान में रखते हुए

हमारा मामला एक्स> 0, उत्तर हैएक्स > 0 ;

3) कब एक्स < 0 получаем: – एक्स / एक्स= 1, यानी ई . -1 = 1, इसलिए,

इस मामले में कोई समाधान नहीं है।

इस तरह, एक्स > 0.

पाठ की शुरुआत में, हम वर्गमूलों के मूल गुणों की समीक्षा करेंगे, और फिर हम वर्गमूलों को सरलीकृत करने वाले व्यंजकों के कुछ जटिल उदाहरणों को देखेंगे।

विषय:समारोह. वर्गमूल गुण

पाठ:जड़ों के साथ अधिक जटिल व्यंजकों को बदलना और सरल बनाना

1. वर्गमूल के गुणों की पुनरावृत्ति

आइए संक्षेप में सिद्धांत को दोहराएं और वर्गमूल के मुख्य गुणों को याद करें।

वर्गमूल के गुण:

1. इसलिए,;

3. ;

4. .

2. जड़ों के साथ भावों को सरल बनाने के उदाहरण

आइए इन गुणों का उपयोग करने के उदाहरणों पर चलते हैं।

उदाहरण 1: एक व्यंजक को सरल कीजिए .

समाधान। सरल बनाने के लिए, संख्या 120 को प्रमुख कारकों में विघटित किया जाना चाहिए:

हम संगत सूत्र के अनुसार योग का वर्ग खोलेंगे:

उदाहरण 2: एक व्यंजक को सरल कीजिए .

समाधान। हम इस बात को ध्यान में रखते हैं कि इस अभिव्यक्ति का चर के सभी संभावित मूल्यों के लिए कोई मतलब नहीं है, क्योंकि इस अभिव्यक्ति में वर्गमूल और अंश शामिल हैं, जो स्वीकार्य मूल्यों की सीमा के "संकुचन" की ओर जाता है। ओडीजेड: ().

हम अभिव्यक्ति को कोष्ठक में एक सामान्य भाजक में लाते हैं और अंतिम अंश के अंश को वर्गों के अंतर के रूप में लिखते हैं:

पर।

उत्तर। पर।

उदाहरण 3: एक व्यंजक को सरल कीजिए .

समाधान। यह देखा जा सकता है कि अंश के दूसरे कोष्ठक का एक अजीब रूप है और इसे सरल बनाने की आवश्यकता है, आइए समूहीकरण विधि का उपयोग करके इसे कारक बनाने का प्रयास करें।

उभयनिष्ठ गुणनखंड निकालने में सक्षम होने के लिए, हमने गुणनखण्ड करके जड़ों को सरल बनाया। परिणामी अभिव्यक्ति को मूल अंश में बदलें:

भिन्न को घटाने के बाद, हम वर्गों के अंतर का सूत्र लागू करते हैं।

3. तर्कहीनता से छुटकारा पाने का एक उदाहरण

उदाहरण 4. हर में तर्कहीनता (जड़ों) से छुटकारा पाएं: ए); बी) ।

समाधान। क) भाजक में अपरिमेयता से छुटकारा पाने के लिए, अंश के अंश और भाजक दोनों को संयुग्म कारक द्वारा भाजक से गुणा करने की मानक विधि का उपयोग किया जाता है (समान अभिव्यक्ति, लेकिन विपरीत चिह्न के साथ)। यह अंश के हर को वर्गों के अंतर के पूरक के लिए किया जाता है, जो आपको हर में जड़ों से छुटकारा पाने की अनुमति देता है। आइए इसे हमारे मामले में करें:

बी) समान क्रियाएं करें:

उत्तर।; .

4. उपपत्ति के लिए और जटिल मूलक में पूर्ण वर्ग के चयन के लिए एक उदाहरण

उदाहरण 5. समानता सिद्ध कीजिए .

सबूत। आइए वर्गमूल की परिभाषा का उपयोग करें, जिससे यह अनुसरण करता है कि सही अभिव्यक्ति का वर्ग मूल अभिव्यक्ति के बराबर होना चाहिए:

. आइए योग के वर्ग के सूत्र के अनुसार कोष्ठक खोलें:

, हमें सही समीकरण मिलता है।

सिद्ध किया हुआ।

उदाहरण 6. व्यंजक को सरल कीजिए।

समाधान। इस अभिव्यक्ति को आमतौर पर एक जटिल कट्टरपंथी (जड़ के नीचे जड़) कहा जाता है। इस उदाहरण में, आपको रेडिकल व्यंजक से पूर्ण वर्ग का चयन करने के लिए अनुमान लगाने की आवश्यकता है। ऐसा करने के लिए, हम ध्यान दें कि दो शब्दों में यह अंतर के वर्ग के सूत्र में एक दोहरे उत्पाद की भूमिका के लिए एक दावेदार है (अंतर, चूंकि एक ऋण है)। आइए इसे ऐसे उत्पाद के रूप में लिखते हैं: , फिर, पूर्ण वर्ग की शर्तों में से एक होने का दावा करता है, और 1 दूसरे की भूमिका निभाने के लिए।

आइए इस अभिव्यक्ति को जड़ के नीचे रखें।

जड़ों और शक्तियों के साथ अभिव्यक्तियों को परिवर्तित करने के लिए अक्सर जड़ों से शक्तियों तक और इसके विपरीत कूदने की आवश्यकता होती है। इस लेख में, हम विश्लेषण करेंगे कि इस तरह के बदलाव कैसे किए जाते हैं, उनके पीछे क्या है और किन बिंदुओं पर अक्सर त्रुटियां होती हैं। हम यह सब विशिष्ट उदाहरणों के साथ समाधानों के विस्तृत विश्लेषण के साथ प्रदान करेंगे।

पेज नेविगेशन।

भिन्नात्मक घातांक वाले घात से मूल की ओर संक्रमण

भिन्नात्मक घातांक वाली डिग्री से जड़ तक जाने की संभावना डिग्री की परिभाषा से तय होती है। याद करें कि यह कैसे निर्धारित किया जाता है: एक सकारात्मक संख्या की डिग्री एक आंशिक घातांक m / n के साथ होती है, जहाँ m एक पूर्णांक है, और n एक प्राकृतिक संख्या है, इसे m का n-वाँ मूल कहा जाता है, जहाँ a> 0, m∈Z, n∈ N. शून्य की भिन्नात्मक शक्ति को इसी तरह परिभाषित किया गया है , केवल अंतर के साथ कि इस मामले में m को पहले से ही पूर्णांक नहीं, बल्कि प्राकृतिक माना जाता है, ताकि शून्य से विभाजन न हो।

इस प्रकार, डिग्री को हमेशा जड़ से बदला जा सकता है। उदाहरण के लिए, आप से से तक जा सकते हैं, और डिग्री को रूट से बदला जा सकता है। लेकिन आपको अभिव्यक्ति से जड़ तक नहीं जाना चाहिए, क्योंकि शुरुआत में डिग्री का कोई मतलब नहीं है (ऋणात्मक संख्याओं की डिग्री परिभाषित नहीं है), इस तथ्य के बावजूद कि रूट समझ में आता है।

जैसा कि आप देख सकते हैं, संख्याओं की घात से मूल तक के परिवर्तन में कुछ भी मुश्किल नहीं है। इसी तरह, मनमाने भावों के आधार पर भिन्नात्मक घातांक वाली शक्तियों की जड़ों में परिवर्तन किया जाता है। ध्यान दें कि संकेतित संक्रमण मूल अभिव्यक्ति के चरों के ODZ पर किया जाता है। उदाहरण के लिए, अभिव्यक्ति इस अभिव्यक्ति के लिए संपूर्ण ODZ चर x पर रूट द्वारा प्रतिस्थापित किया जा सकता है . और डिग्री से जड़ में जाओ , मूल अभिव्यक्ति के लिए DPV से चर x , y और z के किसी भी सेट के लिए ऐसा प्रतिस्थापन होता है।

जड़ों को शक्तियों से बदलना

रिवर्स प्रतिस्थापन भी संभव है, अर्थात, भिन्नात्मक घातांक के साथ डिग्री द्वारा जड़ों का प्रतिस्थापन। यह समानता पर भी आधारित है, जो इस मामले में दाएं से बाएं, यानी रूप में उपयोग किया जाता है।

सकारात्मक a के लिए, यह संक्रमण स्पष्ट है। उदाहरण के लिए, आप डिग्री को बदल सकते हैं, और रूट से फॉर्म के भिन्नात्मक संकेतक के साथ डिग्री पर जा सकते हैं।

और ऋणात्मक a के लिए, समानता का कोई अर्थ नहीं है, लेकिन जड़ का अर्थ हो सकता है। उदाहरण के लिए, जड़ें समझ में आती हैं, लेकिन उन्हें शक्तियों द्वारा प्रतिस्थापित नहीं किया जा सकता। तो क्या उन्हें सत्ता के भावों में बदला जा सकता है? यह संभव है यदि हम प्रारंभिक परिवर्तन करते हैं, जिसमें उनके नीचे गैर-ऋणात्मक संख्याओं के साथ जड़ों में संक्रमण होता है, जिन्हें बाद में भिन्नात्मक घातांक के साथ डिग्री से बदल दिया जाता है। आइए देखें कि ये प्रारंभिक परिवर्तन क्या हैं और उन्हें कैसे पूरा किया जाए।

जड़ के मामले में, आप निम्नलिखित परिवर्तन कर सकते हैं: . और चूँकि 4 एक धनात्मक संख्या है, अंतिम मूल को एक घात से बदला जा सकता है। और दूसरे मामले में एक ऋणात्मक संख्या से एक विषम डिग्री की जड़ का निर्धारण-ए (इस मामले में, सकारात्मक है), जो समानता द्वारा व्यक्त किया गया है , मूल को एक व्यंजक द्वारा प्रतिस्थापित करने की अनुमति देता है जिसमें दो के घनमूल को पहले से ही एक डिग्री से प्रतिस्थापित किया जा सकता है, और यह रूप ले लेगा।

यह पता लगाना बाकी है कि जड़ें, जिसके तहत भाव स्थित हैं, को आधार पर इन भावों वाली डिग्री से कैसे बदला जाता है। यहां आपको प्रतिस्थापित करने में जल्दबाजी नहीं करनी चाहिए, हमने अक्षर A द्वारा कुछ अभिव्यक्ति को निरूपित किया है। आइए इसका अर्थ स्पष्ट करने के लिए एक उदाहरण लें। कोई समानता के आधार पर जड़ को एक डिग्री से बदलना चाहता है। लेकिन ऐसा प्रतिस्थापन तभी उपयुक्त है जब x−3≥0<0 ) она не подходит, так как формула не имеет смысла для отрицательных a . Если обратить внимание на ОДЗ, то несложно заметить ее сужение при переходе от выражения к выражению , а помните, что мы договорились не прибегать к преобразованиям, сужающим ОДЗ.

सूत्र के ऐसे गलत अनुप्रयोग के कारण, मूल से घात की ओर बढ़ते समय त्रुटियाँ अक्सर होती हैं। उदाहरण के लिए, पाठ्यपुस्तक में, अभिव्यक्ति को एक तर्कसंगत प्रतिपादक के साथ एक डिग्री के रूप में प्रस्तुत करने के लिए कार्य दिया जाता है, और उत्तर दिया जाता है, जो प्रश्न उठाता है, क्योंकि बाधा b>0 स्थिति में सेट नहीं है। और पाठ्यपुस्तक में अभिव्यक्ति से एक संक्रमण है , तर्कहीन अभिव्यक्ति के निम्नलिखित परिवर्तनों के माध्यम से सबसे अधिक संभावना है

अभिव्यक्ति के लिए। अंतिम संक्रमण भी सवाल उठाता है, क्योंकि यह ODZ को संकरा कर देता है।

एक तार्किक प्रश्न उठता है: "ODZ से चर के सभी मूल्यों के लिए जड़ से डिग्री की ओर बढ़ना कैसे सही है"? यह प्रतिस्थापन निम्नलिखित कथनों पर आधारित है:

रिकॉर्ड किए गए परिणामों की पुष्टि करने से पहले, हम जड़ों से घातों तक जाने के लिए उनके उपयोग के कई उदाहरण देते हैं। सबसे पहले, आइए अभिव्यक्ति पर वापस जाएं। इसे से नहीं, बल्कि द्वारा प्रतिस्थापित किया जाना था (इस मामले में, m=2 एक सम पूर्णांक है, n=3 एक प्राकृतिक संख्या है)। एक और उदाहरण: .

अब परिणामों की पुष्टि का वादा किया।

जब m एक विषम पूर्णांक होता है, और n एक धनात्मक पूर्णांक होता है, तब व्यंजक के DPV से चरों के किसी सेट के लिए, व्यंजक A का मान धनात्मक होता है (यदि m<0 ) или неотрицательно (если m>0). इसीलिए, ।

चलिए दूसरे परिणाम पर चलते हैं। मान लीजिए m एक धनात्मक विषम पूर्णांक है और n एक विषम प्राकृत संख्या है। ODZ से वेरिएबल्स के सभी मानों के लिए जिनके लिए एक्सप्रेशन A का मान नॉन-नेगेटिव है, , और जिसके लिए यह नकारात्मक है,

निम्नलिखित परिणाम नकारात्मक और विषम पूर्णांक m और प्राकृतिक विषम n के लिए समान रूप से सिद्ध होता है। ODZ से चर के सभी मूल्यों के लिए जिसके लिए अभिव्यक्ति A का मान धनात्मक है, , और जिसके लिए यह नकारात्मक है,

अंत में, अंतिम परिणाम। मान लीजिए m एक सम पूर्णांक है, n कोई भी प्राकृत संख्या है। ODZ से चर के सभी मूल्यों के लिए जिसके लिए अभिव्यक्ति A का मान धनात्मक है (यदि m<0 ) или неотрицательно (если m>0 ), . और जिसके लिए यह नेगेटिव है, . इस प्रकार, यदि m एक पूर्णांक है, n कोई भी प्राकृतिक संख्या है, तो अभिव्यक्ति के लिए DPV से चर के मानों के किसी भी सेट के लिए इसे प्रतिस्थापित किया जा सकता है।

ग्रंथ सूची।

1. बीजगणितऔर विश्लेषण की शुरुआत: प्रोक। 10-11 कोशिकाओं के लिए। सामान्य शिक्षा संस्थान / ए.एन. कोल्मोगोरोव, ए.एम. अब्रामोव, यू.पी. डुडनित्सिन और अन्य; ईडी। ए.एन. कोलमोगोरोवा.- 14वां संस्करण.- एम.: एनलाइटनमेंट, 2004.- 384 पी.: बीमार.- आईएसबीएन 5-09-013651-3.
2. बीजगणितऔर गणितीय विश्लेषण की शुरुआत। ग्रेड 11: पाठ्यपुस्तक। सामान्य शिक्षा के लिए संस्थान: बुनियादी और प्रोफ़ाइल। स्तर / [यू। एम. कोलयागिन, एम.वी. तकाचेवा, एन.ई. फेडोरोवा, एम.आई. शाबुनिन]; ईडी। ए बी झिझचेंको। - एम।: शिक्षा, 2009. - 336 पी।: बीमार। - आईएसबीएन 979-5-09-016551-8।

बधाई हो: आज हम जड़ों का विश्लेषण करेंगे - 8 वीं कक्षा के सबसे दिमाग उड़ाने वाले विषयों में से एक। :)

बहुत से लोग जड़ों के बारे में भ्रमित हो जाते हैं, इसलिए नहीं कि वे जटिल हैं (जो जटिल है - कुछ परिभाषाएँ और कुछ और गुण), बल्कि इसलिए कि अधिकांश स्कूल की पाठ्यपुस्तकों में जड़ों को ऐसे विलड्स के माध्यम से परिभाषित किया जाता है, जो केवल पाठ्यपुस्तकों के लेखक ही कर सकते हैं। इस स्क्रिबलिंग को समझें। और फिर भी केवल अच्छी व्हिस्की की बोतल के साथ। :)

इसलिए, अब मैं जड़ की सबसे सही और सबसे सक्षम परिभाषा दूंगा - केवल वही जिसे आपको वास्तव में याद रखने की आवश्यकता है। और उसके बाद ही मैं समझाऊंगा: यह सब क्यों आवश्यक है और इसे व्यवहार में कैसे लागू किया जाए।

लेकिन पहले, एक महत्वपूर्ण बिंदु याद रखें, जिसके बारे में पाठ्यपुस्तकों के कई संकलनकर्ता किसी कारण से "भूल जाते हैं":

जड़ें सम कोटि की हो सकती हैं (हमारे पसंदीदा $\sqrt(a)$, साथ ही कोई भी $\sqrt(a)$ और यहां तक ​​कि $\sqrt(a)$) और विषम डिग्री (कोई भी $\sqrt(a)$ , $\ sqrt(क)$ आदि). और विषम कोटि के मूल की परिभाषा सम से कुछ भिन्न है।

यहाँ इस कमबख्त में "कुछ अलग" छिपा है, शायद, जड़ों से जुड़ी सभी त्रुटियों और गलतफहमियों का 95%। तो आइए एक बार और सभी के लिए शब्दावली स्पष्ट करें:

परिभाषा। जड़ भी एनसंख्या $a$ से कोई भी है गैर नकारात्मकएक संख्या $b$ जैसे कि $((b)^(n))=a$। और एक ही संख्या से एक विषम डिग्री की जड़ आम तौर पर कोई भी संख्या $b$ होती है जिसके लिए समान समानता होती है: $((b)^(n))=a$।

किसी भी मामले में, जड़ को इस तरह निरूपित किया जाता है:

\(एक)\]

इस तरह के अंकन में $n$ को रूट एक्सपोनेंट कहा जाता है, और संख्या $a$ को रेडिकल एक्सप्रेशन कहा जाता है। विशेष रूप से, $n=2$ के लिए हमें अपना "पसंदीदा" वर्गमूल मिलता है (वैसे, यह एक समान डिग्री का रूट है), और $n=3$ के लिए हमें एक क्यूबिक रूट (एक विषम डिग्री) मिलता है। जो अक्सर समस्याओं और समीकरणों में भी पाया जाता है।

उदाहरण। वर्गमूल के क्लासिक उदाहरण:

\[\शुरू (संरेखित करें) और \sqrt(4)=2; \\ & \sqrt(81)=9; \\ & \sqrt(256)=16. \\ \end(संरेखित करें)\]

वैसे, $\sqrt(0)=0$ और $\sqrt(1)=1$। $((0)^(2))=0$ और $((1)^(2))=1$ के बाद से यह काफी तार्किक है।

घनमूल भी आम हैं - उनसे डरो मत:

\[\शुरू (संरेखित करें) और \sqrt(27)=3; \\ & \sqrt(-64)=-4; \\ & \sqrt(343)=7. \\ \end(संरेखित करें)\]

खैर, कुछ "विदेशी उदाहरण":

\[\शुरू (संरेखित करें) और \sqrt(81)=3; \\ & \sqrt(-32)=-2. \\ \end(संरेखित करें)\]

यदि आप सम और विषम डिग्री के बीच के अंतर को नहीं समझते हैं, तो परिभाषा को फिर से पढ़ें। बहुत जरुरी है!

इस बीच, हम जड़ों की एक अप्रिय विशेषता पर विचार करेंगे, जिसके कारण हमें सम और विषम घातांकों के लिए एक अलग परिभाषा प्रस्तुत करने की आवश्यकता थी।

हमें जड़ों की आवश्यकता क्यों है?

परिभाषा पढ़ने के बाद, कई छात्र पूछेंगे: "गणितज्ञों ने इसका आविष्कार करते समय क्या धूम्रपान किया था?" और वास्तव में: हमें इन सभी जड़ों की आवश्यकता क्यों है?

इस प्रश्न का उत्तर देने के लिए, आइए एक पल के लिए प्राथमिक विद्यालय में वापस जाएँ। याद रखें: उन दूर के समय में, जब पेड़ हरे थे और पकौड़ी स्वादिष्ट थे, हमारी मुख्य चिंता संख्याओं को सही ढंग से गुणा करना था। ठीक है, "पाँच बटा पाँच - पच्चीस" की भावना में कुछ, बस इतना ही। लेकिन आखिरकार, आप संख्याओं को जोड़े में नहीं, बल्कि तीन, चार और आम तौर पर पूरे सेट में गुणा कर सकते हैं:

\[\शुरू (संरेखित करें) और 5\cdot 5=25; \\ & 5\cdot 5\cdot 5=125; \\ & 5\cdot 5\cdot 5\cdot 5=625; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5=3125; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5=15\ 625. \end(संरेखित करें)\]

हालाँकि, यह बात नहीं है। तरकीब अलग है: गणितज्ञ आलसी लोग होते हैं, इसलिए उन्हें दस फाइव का गुणा इस तरह लिखना पड़ा:

इसलिए वे डिग्री लेकर आए। लंबी स्ट्रिंग के बजाय कारकों की संख्या को सुपरस्क्रिप्ट के रूप में क्यों नहीं लिखते? इस तरह:

यह बहुत सुविधाजनक है! सभी गणना कई बार कम हो जाती हैं, और आप कुछ 5 183 लिखने के लिए नोटबुक की चर्मपत्र शीट्स का एक गुच्छा खर्च नहीं कर सकते हैं। इस तरह की प्रविष्टि को संख्या की डिग्री कहा जाता था, इसमें गुणों का एक समूह पाया गया था, लेकिन खुशी अल्पकालिक थी।

डिग्री की "खोज" के बारे में आयोजित एक भव्य शराब के बाद, कुछ विशेष रूप से पत्थरबाज़ गणितज्ञों ने अचानक पूछा: "क्या होगा यदि हम किसी संख्या की डिग्री जानते हैं, लेकिन हम स्वयं संख्या नहीं जानते हैं?" दरअसल, अगर हम जानते हैं कि एक निश्चित संख्या $b$, उदाहरण के लिए, 243 को 5 वीं शक्ति देता है, तो हम कैसे अनुमान लगा सकते हैं कि संख्या $b$ खुद किसके बराबर है?

यह समस्या पहली नज़र में लगने की तुलना में कहीं अधिक वैश्विक निकली। क्योंकि यह पता चला है कि अधिकांश "तैयार-निर्मित" डिग्रियों के लिए ऐसी "प्रारंभिक" संख्याएँ नहीं हैं। अपने लिए जज करें:

\[\शुरू (संरेखित करें) और ((बी)^(3))=27\Rightarrow b=3\cdot 3\cdot 3\Rightarrow b=3; \\ & ((बी)^(3))=64\Rightarrow b=4\cdot 4\cdot 4\Rightarrow b=4. \\ \end(संरेखित करें)\]

क्या होगा यदि $((बी)^(3))=50$? यह पता चला है कि आपको एक निश्चित संख्या खोजने की जरूरत है, जो तीन बार खुद से गुणा करने पर हमें 50 देगा। लेकिन यह संख्या क्या है? यह स्पष्ट रूप से 3 से बड़ा है क्योंकि 3 3 = 27< 50. С тем же успехом оно меньше 4, поскольку 4 3 = 64 >50. यानी यह संख्या तीन और चार के बीच कहीं है, लेकिन यह किसके बराबर है - FIG आप समझ जाएंगे।

यही कारण है कि गणितज्ञ $n$-th जड़ों के साथ आए। यही कारण है कि रेडिकल आइकन $\sqrt(*)$ पेश किया गया था। उसी संख्या को निरूपित करने के लिए $b$, जो, निर्दिष्ट शक्ति के लिए, हमें पहले से ज्ञात मान देगा

\[\sqrt[n](a)=b\Rightarrow ((b)^(n))=a\]

मैं बहस नहीं करता: अक्सर इन जड़ों पर आसानी से विचार किया जाता है - हमने ऐसे कई उदाहरण ऊपर देखे हैं। लेकिन फिर भी, ज्यादातर मामलों में, यदि आप एक मनमाना संख्या के बारे में सोचते हैं, और फिर उसमें से एक मनमाना डिग्री की जड़ निकालने की कोशिश करते हैं, तो आप एक क्रूर बमर के लिए हैं।

वहां क्या है! यहां तक ​​​​कि सबसे सरल और सबसे परिचित $\sqrt(2)$ को हमारे सामान्य रूप में - पूर्णांक या अंश के रूप में प्रदर्शित नहीं किया जा सकता है। और अगर आप इस नंबर को कैलकुलेटर में चलाते हैं, तो आप इसे देखेंगे:

\[\sqrt(2)=1.414213562...\]

जैसा कि आप देख सकते हैं, दशमलव बिंदु के बाद संख्याओं का एक अंतहीन क्रम होता है जो किसी भी तर्क का पालन नहीं करता है। बेशक, आप अन्य नंबरों के साथ जल्दी से तुलना करने के लिए इस नंबर को गोल कर सकते हैं। उदाहरण के लिए:

\[\sqrt(2)=1.4142...\लगभग 1.4 \lt 1.5\]

या यहाँ एक और उदाहरण है:

\[\sqrt(3)=1.73205...\लगभग 1.7 \gt 1.5\]

लेकिन ये सभी गोलाई, सबसे पहले, बल्कि खुरदरी हैं; और दूसरी बात, आपको अनुमानित मूल्यों के साथ काम करने में सक्षम होने की भी आवश्यकता है, अन्यथा आप गैर-स्पष्ट त्रुटियों का एक गुच्छा पकड़ सकते हैं (वैसे, प्रोफ़ाइल परीक्षा में तुलना और गोलाई का कौशल आवश्यक रूप से जांचा जाता है)।

इसलिए, गंभीर गणित में, कोई भी जड़ों के बिना नहीं कर सकता - वे सभी वास्तविक संख्याओं के सेट के समान प्रतिनिधि हैं $\mathbb(R)$, जैसे अंश और पूर्णांक जिन्हें हम लंबे समय से जानते हैं।

मूल को $\frac(p)(q)$ के रूप में भिन्न के रूप में निरूपित करने की असंभवता का अर्थ है कि यह मूल एक परिमेय संख्या नहीं है। इस तरह की संख्याओं को अपरिमेय कहा जाता है, और उन्हें एक कट्टरपंथी, या विशेष रूप से इसके लिए डिज़ाइन किए गए अन्य निर्माणों (लघुगणक, डिग्री, सीमा, आदि) की सहायता के अलावा सटीक रूप से प्रदर्शित नहीं किया जा सकता है। लेकिन उस पर फिर कभी।

कुछ उदाहरणों पर विचार करें, जहां सभी गणनाओं के बाद भी अपरिमेय संख्याएं उत्तर में बनी रहेंगी।

\[\शुरू (संरेखित) और \sqrt(2+\sqrt(27))=\sqrt(2+3)=\sqrt(5)\लगभग 2,236... \\ & \sqrt(-32 ))=\sqrt(-2)\approx -1,2599... \\ \end(संरेखित करें)\]

स्वाभाविक रूप से, जड़ की उपस्थिति से, यह अनुमान लगाना लगभग असंभव है कि दशमलव बिंदु के बाद कौन सी संख्याएँ आएंगी। हालांकि, कैलकुलेटर पर गणना करना संभव है, लेकिन यहां तक ​​कि सबसे उन्नत तिथि कैलकुलेटर भी हमें एक अपरिमेय संख्या के पहले कुछ अंक ही देता है। इसलिए, उत्तरों को $\sqrt(5)$ और $\sqrt(-2)$ के रूप में लिखना अधिक सही है।

यही उनके लिए आविष्कार किया गया था। उत्तर लिखना आसान बनाने के लिए।

दो परिभाषाओं की आवश्यकता क्यों है?

चौकस पाठक शायद पहले ही देख चुके हैं कि उदाहरणों में दिए गए सभी वर्गमूल धनात्मक संख्याओं से लिए गए हैं। ठीक है, कम से कम शून्य से। लेकिन घन जड़ों को पूरी तरह से किसी भी संख्या से निकाला जाता है - सकारात्मक भी, नकारात्मक भी।

ये क्यों हो रहा है? फ़ंक्शन $y=((x)^(2))$ के ग्राफ़ पर एक नज़र डालें:

द्विघात फलन का ग्राफ दो मूल देता है: धनात्मक और ऋणात्मक

आइए इस ग्राफ का उपयोग करके $\sqrt(4)$ की गणना करने का प्रयास करें। ऐसा करने के लिए, एक क्षैतिज रेखा $y=4$ (लाल रंग में चिह्नित) ग्राफ पर खींची जाती है, जो पैराबोला को दो बिंदुओं पर काटती है: $((x)_(1))=2$ और $((x) _(2)) = -2$। यह काफी तार्किक है, चूंकि

पहली संख्या के साथ सब कुछ स्पष्ट है - यह धनात्मक है, इसलिए यह मूल है:

लेकिन फिर दूसरे बिंदु का क्या करें? क्या 4 की एक साथ दो जड़ें हैं? आखिरकार, यदि हम संख्या -2 का वर्ग करते हैं, तो हमें भी 4 प्राप्त होता है। फिर $\sqrt(4)=-2$ क्यों नहीं लिखते? और शिक्षक ऐसे अभिलेखों को क्यों देखते हैं जैसे कि वे आपको खाना चाहते हैं? :)

परेशानी यह है कि यदि कोई अतिरिक्त शर्तें नहीं लगाई जाती हैं, तो चारों के दो वर्गमूल होंगे - धनात्मक और ऋणात्मक। और किसी भी धनात्मक संख्या में भी उनमें से दो होंगे। लेकिन ऋणात्मक संख्याओं की जड़ें बिल्कुल नहीं होंगी - यह उसी ग्राफ से देखा जा सकता है, क्योंकि परवलय कभी भी अक्ष के नीचे नहीं आता है वाई, अर्थात। नकारात्मक मान नहीं लेता है।

समान घातांक वाली सभी जड़ों के लिए समान समस्या होती है:

1. सख्ती से बोलते हुए, प्रत्येक सकारात्मक संख्या में दो जड़ें एक समान एक्सपोनेंट $n$ के साथ होंगी;
2. ऋणात्मक संख्याओं से, $n$ वाला मूल बिल्कुल भी नहीं निकाला जाता है।

यही कारण है कि एक सम मूल $n$ की परिभाषा विशेष रूप से निर्धारित करती है कि उत्तर एक गैर-ऋणात्मक संख्या होनी चाहिए। इस तरह हम अस्पष्टता से छुटकारा पा लेते हैं।

लेकिन विषम $n$ के लिए ऐसी कोई समस्या नहीं है। इसे देखने के लिए, आइए फ़ंक्शन $y=((x)^(3))$ के ग्राफ़ पर एक नज़र डालें:

घन परवलय किसी भी मान को ग्रहण करता है, इसलिए घनमूल को किसी भी संख्या से लिया जा सकता है

इस ग्राफ से दो निष्कर्ष निकाले जा सकते हैं:

1. एक घन परवलय की शाखाएँ, सामान्य के विपरीत, दोनों दिशाओं में अनंत तक जाती हैं - ऊपर और नीचे दोनों। इसलिए, हम जिस भी ऊँचाई पर एक क्षैतिज रेखा खींचते हैं, यह रेखा निश्चित रूप से हमारे ग्राफ के साथ प्रतिच्छेद करेगी। इसलिए, घनमूल हमेशा किसी भी संख्या से लिया जा सकता है;
2. इसके अलावा, ऐसा चौराहा हमेशा अद्वितीय होगा, इसलिए आपको यह सोचने की ज़रूरत नहीं है कि किस नंबर को "सही" रूट पर विचार करना है, और कौन सा स्कोर करना है। यही कारण है कि एक विषम डिग्री के लिए जड़ों की परिभाषा एक सम की तुलना में सरल है (कोई गैर-नकारात्मक आवश्यकता नहीं है)।

यह अफ़सोस की बात है कि अधिकांश पाठ्य पुस्तकों में इन सरल बातों को नहीं समझाया गया है। इसके बजाय, हमारा दिमाग सभी प्रकार की अंकगणितीय जड़ों और उनके गुणों से ऊपर उठने लगता है।

हां, मैं बहस नहीं करता: अंकगणितीय जड़ क्या है - आपको भी जानने की जरूरत है। और मैं इसके बारे में एक अलग पाठ में विस्तार से बात करूंगा। आज हम इसके बारे में भी बात करेंगे, क्योंकि इसके बिना $n$-th बहुलता की जड़ों पर सभी विचार अधूरे होंगे।

लेकिन पहले आपको ऊपर दी गई परिभाषा को स्पष्ट रूप से समझने की आवश्यकता है। अन्यथा शब्दों की अधिकता के कारण आपके दिमाग में ऐसी गड़बड़ी शुरू हो जाएगी कि अंत में आप कुछ भी नहीं समझ पाएंगे।

और आपको केवल सम और विषम संख्याओं के बीच का अंतर समझने की आवश्यकता है। इसलिए, एक बार फिर हम सब कुछ एकत्र करेंगे जो आपको वास्तव में जड़ों के बारे में जानने की जरूरत है:

1. एक सम मूल केवल एक गैर-ऋणात्मक संख्या से ही अस्तित्व में आता है और स्वयं हमेशा एक गैर-ऋणात्मक संख्या होती है। ऋणात्मक संख्याओं के लिए, ऐसी जड़ अपरिभाषित होती है।
2. लेकिन एक विषम डिग्री की जड़ किसी भी संख्या से मौजूद होती है और स्वयं कोई भी संख्या हो सकती है: सकारात्मक संख्याओं के लिए यह सकारात्मक है, और ऋणात्मक संख्याओं के लिए, कैप संकेत के रूप में, यह नकारात्मक है।

क्या यह मुश्किल है? नहीं, यह मुश्किल नहीं है। साफ़? हाँ, यह स्पष्ट है! इसलिए, अब हम गणनाओं के साथ थोड़ा अभ्यास करेंगे।

बुनियादी गुण और सीमाएं

जड़ों में बहुत सारे अजीब गुण और प्रतिबंध हैं - यह एक अलग सबक होगा। इसलिए, अब हम केवल सबसे महत्वपूर्ण "चिप" पर विचार करेंगे, जो केवल समान घातांक वाली जड़ों पर लागू होता है। हम इस गुण को सूत्र के रूप में लिखते हैं:

\[\sqrt((((x)^(2n)))=\बाएं| एक्स\दाएं|\]

दूसरे शब्दों में, यदि हम किसी संख्या को एक सम घात तक बढ़ाते हैं, और फिर उसमें से समान कोटि का मूल निकालते हैं, तो हमें मूल संख्या नहीं, बल्कि उसका मापांक प्राप्त होगा। यह एक सरल प्रमेय है जिसे साबित करना आसान है (यह अलग से गैर-नकारात्मक $x$ पर विचार करने के लिए पर्याप्त है, और फिर अलग से नकारात्मक पर विचार करें)। शिक्षक लगातार इसके बारे में बात करते हैं, यह हर स्कूल की पाठ्यपुस्तक में दिया जाता है। लेकिन जैसे ही अपरिमेय समीकरणों (अर्थात करणी के चिह्न वाले समीकरण) को हल करने की बात आती है तो छात्र इस सूत्र को एक साथ भूल जाते हैं।

इस मुद्दे को विस्तार से समझने के लिए, आइए एक मिनट के लिए सभी सूत्रों को भूल जाएं और दो संख्याओं को आगे गिनने का प्रयास करें:

\[\sqrt((((3)^(4)))=?\चौथा \sqrt(((\बाएं(-3 \दाएं))^(4)))=?\]

ये बहुत ही साधारण उदाहरण हैं। पहला उदाहरण अधिकांश लोगों द्वारा हल किया जाएगा, लेकिन दूसरे पर, बहुत से लोग टिके रहते हैं। ऐसी किसी भी बकवास को बिना किसी समस्या के हल करने के लिए, हमेशा प्रक्रिया पर विचार करें:

1. सबसे पहले, संख्या को चौथी शक्ति तक बढ़ाया जाता है। खैर, यह आसान है। एक नई संख्या प्राप्त होगी, जिसे गुणन सारणी में भी पाया जा सकता है;
2. और अब इस नई संख्या से चौथी डिग्री का मूल निकालना आवश्यक है। वे। जड़ों और डिग्री की कोई "कमी" नहीं है - ये क्रमिक क्रियाएं हैं।

आइए पहली अभिव्यक्ति से निपटें: $\sqrt(((3)^(4)))$। जाहिर है, आपको पहले रूट के तहत अभिव्यक्ति की गणना करने की आवश्यकता है:

\[(((3)^(4))=3\cdot 3\cdot 3\cdot 3=81\]

फिर हम संख्या 81 का चौथा मूल निकालते हैं:

अब दूसरी अभिव्यक्ति के साथ भी ऐसा ही करते हैं। सबसे पहले, हम संख्या -3 को चौथी शक्ति तक बढ़ाते हैं, जिसके लिए हमें इसे 4 बार गुणा करने की आवश्यकता होती है:

\[((\बाएं(-3 \दाएं))^(4))=\बाएं(-3 \दाएं)\cdot \बाएं(-3 \दाएं)\cdot \बाएं(-3 \दाएं)\cdot \ बायां (-3 \ दायां) = 81 \]

हमें एक सकारात्मक संख्या मिली, क्योंकि उत्पाद में कुल नुकसान की संख्या 4 टुकड़े हैं, और वे सभी एक दूसरे को रद्द कर देंगे (आखिरकार, एक ऋण से एक ऋण एक प्लस देता है)। अगला, जड़ को फिर से निकालें:

सिद्धांत रूप में, यह पंक्ति नहीं लिखी जा सकती थी, क्योंकि इसमें कोई दिमाग नहीं है कि उत्तर समान होगा। वे। एक ही सम शक्ति की एक समान जड़ "माइनस" को "जल" देती है, और इस अर्थ में परिणाम सामान्य मॉड्यूल से अप्रभेद्य है:

\[\शुरू(संरेखित करें) और \sqrt(((3)^(4)))=\बाएं| 3\दाएं|=3; \\ & \sqrt(((\बाएं(-3 \दाएं))^(4))=\बाएं| -3 \दाहिना|=3. \\ \end(संरेखित करें)\]

ये परिकलन सम कोटि के मूल की परिभाषा के साथ अच्छे समझौते में हैं: परिणाम हमेशा गैर-ऋणात्मक होता है, और करणी चिह्न भी हमेशा एक गैर-ऋणात्मक संख्या होती है। अन्यथा, रूट परिभाषित नहीं है।

संचालन के क्रम पर ध्यान दें

1. संकेतन $\sqrt(((a)^(2)))$ का अर्थ है कि हम पहले संख्या $a$ का वर्ग करते हैं, और फिर परिणामी मूल्य का वर्गमूल लेते हैं। इसलिए, हम यह सुनिश्चित कर सकते हैं कि एक गैर-ऋणात्मक संख्या हमेशा मूल चिह्न के नीचे बैठती है, क्योंकि $((a)^(2))\ge 0$ वैसे भी;
2. लेकिन नोटेशन $((\बाएं(\sqrt(a) \right))^(2))$, इसके विपरीत, इसका मतलब है कि हम पहले एक निश्चित संख्या $a$ से रूट निकालते हैं और उसके बाद ही परिणाम को स्क्वायर करते हैं। इसलिए, संख्या $a$ किसी भी स्थिति में ऋणात्मक नहीं हो सकती - यह परिभाषा में अंतर्निहित एक अनिवार्य आवश्यकता है।

इस प्रकार, किसी भी मामले में जड़ों और डिग्री को विचारपूर्वक कम नहीं करना चाहिए, जिससे मूल अभिव्यक्ति को "सरल" माना जाता है। क्योंकि यदि मूल के नीचे कोई ऋणात्मक संख्या हो और उसका घातांक सम हो, तो हमें बहुत समस्याएँ आएंगी।

हालाँकि, ये सभी समस्याएं केवल संकेतकों के लिए भी प्रासंगिक हैं।

मूल चिह्न के नीचे से ऋण चिह्न हटाना

स्वाभाविक रूप से, विषम घातांक वाली जड़ों की भी अपनी विशेषता होती है, जो सिद्धांत रूप में, यहां तक ​​\u200b\u200bकि मौजूद नहीं है। अर्थात्:

\[\sqrt(-a)=-\sqrt(ए)\]

संक्षेप में, आप एक विषम डिग्री की जड़ों के चिह्न के नीचे से ऋण निकाल सकते हैं। यह एक बहुत ही उपयोगी संपत्ति है जो आपको सभी नुकसानों को "फेंकने" की अनुमति देती है:

\[\शुरू (संरेखित) और \sqrt(-8)=-\sqrt(8)=-2; \\ & \sqrt(-27)\cdot \sqrt(-32)=-\sqrt(27)\cdot \बाएं (-\sqrt(32) \दाएं)= \\ & =\sqrt(27)\cdot \sqrt(32)= \\ & =3\cdot 2=6. \ अंत (संरेखित करें) \]

यह सरल संपत्ति कई गणनाओं को बहुत सरल करती है। अब आपको चिंता करने की ज़रूरत नहीं है: क्या होगा अगर एक नकारात्मक अभिव्यक्ति जड़ के नीचे हो जाती है, और जड़ की डिग्री भी निकल जाती है? यह जड़ों के बाहर के सभी नुकसानों को "फेंकने" के लिए पर्याप्त है, जिसके बाद उन्हें एक दूसरे से गुणा किया जा सकता है, विभाजित किया जा सकता है और आम तौर पर कई संदिग्ध चीजें की जा सकती हैं, जो "क्लासिक" जड़ों के मामले में हमें एक त्रुटि की ओर ले जाने की गारंटी है। .

और यहाँ एक और परिभाषा सामने आती है - वही जिसके साथ अधिकांश स्कूल तर्कहीन अभिव्यक्तियों का अध्ययन शुरू करते हैं। और जिसके बिना हमारी रीज़निंग अधूरी होगी। मिलना!

अंकगणितीय जड़

आइए एक पल के लिए मान लें कि केवल धनात्मक संख्याएं या चरम मामलों में, शून्य मूल चिह्न के अंतर्गत हो सकता है। आइए सम / विषम संकेतकों पर स्कोर करें, ऊपर दी गई सभी परिभाषाओं पर स्कोर करें - हम केवल गैर-ऋणात्मक संख्याओं के साथ काम करेंगे। फिर क्या?

और फिर हमें अंकगणितीय जड़ मिलती है - यह आंशिक रूप से हमारी "मानक" परिभाषाओं के साथ प्रतिच्छेद करती है, लेकिन फिर भी उनसे भिन्न होती है।

परिभाषा। एक गैर-ऋणात्मक संख्या $a$ की $n$th डिग्री का एक अंकगणितीय मूल एक गैर-ऋणात्मक संख्या $b$ है जैसे कि $((b)^(n))=a$।

जैसा कि आप देख सकते हैं, हमें अब समानता में कोई दिलचस्पी नहीं है। इसके बजाय, एक नया प्रतिबंध सामने आया: कट्टरपंथी अभिव्यक्ति अब हमेशा गैर-नकारात्मक है, और जड़ भी गैर-नकारात्मक है।

यह समझने के लिए कि अंकगणितीय जड़ सामान्य से कैसे भिन्न होती है, पहले से परिचित वर्ग और घन परवलय के रेखांकन पर एक नज़र डालें:

मूल खोज क्षेत्र - गैर-ऋणात्मक संख्याएँ

जैसा कि आप देख सकते हैं, अब से, हम केवल ग्राफ़ के उन टुकड़ों में रुचि रखते हैं जो पहले समन्वय तिमाही में स्थित हैं - जहां निर्देशांक $x$ और $y$ सकारात्मक हैं (या कम से कम शून्य)। आपको यह समझने के लिए संकेतक को देखने की आवश्यकता नहीं है कि क्या हमें ऋणात्मक संख्या को रूट करने का अधिकार है या नहीं। क्योंकि नकारात्मक संख्याओं को अब सिद्धांत रूप में नहीं माना जाता है।

आप पूछ सकते हैं: "ठीक है, हमें इस तरह की परिभाषा की आवश्यकता क्यों है?" या: "हम ऊपर दी गई मानक परिभाषा से क्यों नहीं चल सकते?"

खैर, मैं सिर्फ एक संपत्ति दूंगा, जिसके कारण नई परिभाषा उपयुक्त हो जाती है। उदाहरण के लिए, घातांक नियम:

\[\sqrt[n](ए)=\sqrt(((ए)^(के)))\]

कृपया ध्यान दें: हम मूल अभिव्यक्ति को किसी भी शक्ति तक बढ़ा सकते हैं और उसी समय रूट एक्सपोनेंट को उसी शक्ति से गुणा कर सकते हैं - और परिणाम एक ही संख्या होगी! यहाँ कुछ उदाहरण हैं:

\[\शुरू (संरेखित करें) और \sqrt(5)=\sqrt((((5)^(2)))=\sqrt(25) \\ & \sqrt(2)=\sqrt(((2)^) (4)))=\sqrt(16) \\ \end(संरेखित करें)\]

अच्छा, इसमें गलत क्या है? हम इसे पहले क्यों नहीं कर सके? यहाँ पर क्यों। एक साधारण अभिव्यक्ति पर विचार करें: $\sqrt(-2)$ एक संख्या है जो हमारे शास्त्रीय अर्थों में काफी सामान्य है, लेकिन अंकगणितीय रूट के दृष्टिकोण से बिल्कुल अस्वीकार्य है। आइए इसे रूपांतरित करने का प्रयास करें:

$\शुरू (संरेखित) और \sqrt(-2)=-\sqrt(2)=-\sqrt(((2)^(2)))=-\sqrt(4) \lt 0; \\ & \sqrt(-2)=\sqrt(((\बाएं(-2 \दाएं))^(2))=\sqrt(4) \gt 0. \\ \end(संरेखित करें)$

जैसा कि आप देख सकते हैं, पहले मामले में, हमने माइनस को रेडिकल के नीचे से निकाला (हमारे पास हर अधिकार है, क्योंकि सूचक विषम है), और दूसरे में, हमने उपरोक्त सूत्र का उपयोग किया। वे। गणित की दृष्टि से सब कुछ नियमों के अनुसार होता है।

डब्ल्यूटीएफ ?! एक ही संख्या धनात्मक और ऋणात्मक दोनों कैसे हो सकती है? बिल्कुल नहीं। यह सिर्फ इतना है कि घातांक सूत्र, जो धनात्मक संख्याओं और शून्य के लिए बहुत अच्छा काम करता है, ऋणात्मक संख्याओं के मामले में पूर्ण विधर्म देना शुरू कर देता है।

यहाँ, इस तरह की अस्पष्टता से छुटकारा पाने के लिए, वे अंकगणितीय जड़ों के साथ आए। एक अलग बड़ा पाठ उनके लिए समर्पित है, जहाँ हम उनके सभी गुणों पर विस्तार से विचार करते हैं। इसलिए अब हम उन पर ध्यान नहीं देंगे - वैसे भी पाठ बहुत लंबा हो गया।

बीजगणितीय जड़: उनके लिए जो अधिक जानना चाहते हैं

मैंने लंबे समय तक सोचा: इस विषय को एक अलग पैराग्राफ में बनाया जाए या नहीं। अंत में मैंने यहां से जाने का फैसला किया। यह सामग्री उन लोगों के लिए अभिप्रेत है जो जड़ों को और भी बेहतर समझना चाहते हैं - अब औसत "स्कूल" स्तर पर नहीं, बल्कि ओलंपियाड के करीब के स्तर पर।

तो: एक संख्या से $n$-th डिग्री की जड़ की "शास्त्रीय" परिभाषा और सम और विषम संकेतकों में संबद्ध विभाजन के अलावा, एक और "वयस्क" परिभाषा है, जो समता पर निर्भर नहीं करती है और अन्य सूक्ष्मताएं बिल्कुल। इसे बीजगणितीय मूल कहते हैं।

परिभाषा। एक बीजगणित $n$-th किसी भी $a$ की जड़ सभी संख्याओं का सेट है $b$ ऐसा है कि $((b)^(n))=a$। ऐसी जड़ों के लिए कोई अच्छी तरह से स्थापित पदनाम नहीं है, इसलिए बस शीर्ष पर डैश लगाएं:

\[\overline(\sqrt[n](a))=\left\( b\left| b\in \mathbb(R);((b)^(n))=a \right. \right\) \]

पाठ की शुरुआत में दी गई मानक परिभाषा से मूलभूत अंतर यह है कि बीजगणितीय जड़ एक विशिष्ट संख्या नहीं है, बल्कि एक सेट है। और चूँकि हम वास्तविक संख्याओं के साथ कार्य कर रहे हैं, यह समुच्चय केवल तीन प्रकार का है:

1. खाली सेट। तब होता है जब एक ऋणात्मक संख्या से सम डिग्री का बीजगणितीय मूल ज्ञात करना आवश्यक होता है;
2. एक एकल तत्व से मिलकर एक सेट। विषम शक्तियों की सभी जड़ें, साथ ही शून्य से भी शक्तियों की जड़ें इस श्रेणी में आती हैं;
3. अंत में, सेट में दो नंबर शामिल हो सकते हैं - वही $((x)_(1))$ और $((x)_(2))=-((x)_(1))$ जो हमने चार्ट द्विघात समारोह। तदनुसार, ऐसा संरेखण तभी संभव है जब किसी धनात्मक संख्या से सम अंश का मूल निकाला जाए।

अंतिम मामला अधिक विस्तृत विचार के योग्य है। आइए अंतर को समझने के लिए कुछ उदाहरण गिनें।

उदाहरण। गणना भाव:

\[\overline(\sqrt(4));\quad \overline(\sqrt(-27));\quad \overline(\sqrt(-16)).\]

समाधान। पहली अभिव्यक्ति सरल है:

\[\overline(\sqrt(4))=\बाएं\( 2;-2 \दाएं\)\]

यह दो नंबर हैं जो सेट का हिस्सा हैं। क्योंकि उनमें से प्रत्येक का वर्ग एक चौका देता है।

\[\overline(\sqrt(-27))=\बाएं\( -3 \दाएं\)\]

यहां हम एक सेट देखते हैं जिसमें केवल एक संख्या होती है। यह काफी तार्किक है, क्योंकि जड़ का प्रतिपादक विषम है।

अंत में, अंतिम अभिव्यक्ति:

\[\overline(\sqrt(-16))=\varnothing \]

हमें एक खाली सेट मिला। क्योंकि एक भी वास्तविक संख्या नहीं है, जिसे जब चौथे (अर्थात, सम!) घात तक बढ़ाया जाए, तो हमें एक ऋणात्मक संख्या -16 मिलेगी।

अंतिम नोट। कृपया ध्यान दें: यह संयोग से नहीं था कि मैंने हर जगह नोट किया कि हम वास्तविक संख्याओं के साथ काम कर रहे हैं। क्योंकि वहाँ भी जटिल संख्याएँ हैं - $\sqrt(-16)$ और वहाँ कई अन्य अजीब चीजों की गणना करना काफी संभव है।

हालांकि, गणित के आधुनिक स्कूली पाठ्यक्रम में जटिल संख्याएं लगभग कभी नहीं पाई जाती हैं। उन्हें अधिकांश पाठ्य पुस्तकों से हटा दिया गया है क्योंकि हमारे अधिकारी इस विषय को "समझने में बहुत कठिन" मानते हैं।

बस इतना ही। अगले पाठ में, हम जड़ों के सभी प्रमुख गुणों को देखेंगे और अंत में अपरिमेय व्यंजकों को सरल बनाना सीखेंगे। :)