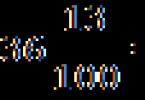Topic: Decimal fractions. Adding and subtracting decimals
Lesson: Decimal notation of fractional numbers
The denominator of a fraction can be expressed by any natural number. Fractional numbers in which the denominator is expressed as 10; 100; 1000;…, where n, we agreed to write it without a denominator. Any fractional number whose denominator is 10; 100; 1000, etc. (that is, a one followed by several zeros) can be represented in decimal notation (as a decimal). First write the whole part, then the numerator of the fractional part, and the whole part is separated from the fraction by a comma.
For example,
![]()
If an entire part is missing, i.e. If the fraction is proper, then the whole part is written as 0.
To write a decimal correctly, the numerator of the fraction must have as many digits as there are zeros in the fraction.
![]()
1. Write as a decimal.
![]()
2. Represent a decimal as a fraction or mixed number.
3. Read the decimals.
12.4 - 12 point 4;
0.3 - 0 point 3;
1.14 - 1 point 14 hundredths;
2.07 - 2 point 7 hundredths;
0.06 - 0 point 6 hundredths;
0.25 - 0 point 25;
1.234 - 1 point 234 thousandths;
1.230 - 1 point 230 thousandths;
1.034 - 1 point 34 thousandths;
1.004 - 1 point 4 thousandths;
1.030 - 1 point 30 thousandths;
0.010101 - 0 point 10101 millionths.
4. Move the comma in each digit 1 place to the left and read the numbers.
34,1; 310,2; 11,01; 10,507; 2,7; 3,41; 31,02; 1,101; 1,0507; 0,27.
5. Move the comma in each number 1 place to the right and read the resulting number.
1,37; 0,1401; 3,017; 1,7; 350,4; 13,7; 1,401; 30,17; 17; 3504.
6. Express in meters and centimeters.
3.28 m = 3 m + .
7. Express in tons and kilograms.
24.030 t = 24 t.
8. Write the quotient as a decimal fraction.
1710: 100 = ![]() ;
;
64: 10000 = ![]()
803: 100 = ![]()
407: 10 = ![]()
9. Express in dm.
5 dm 6 cm = 5 dm + ![]() ;
;
9 mm = ![]()
fractional number.
Decimal notation of a fractional number is a set of two or more digits from $0$ to $9$, between which there is a so-called \textit (decimal point).
Example 1
For example, $35.02$; $100.7$; $123\456.5$; $54.89$.
The leftmost digit in the decimal notation of a number cannot be zero, the only exception being when the decimal point is immediately after the first digit $0$.
Example 2
For example, $0.357$; $0.064$.
Often the decimal point is replaced with a decimal point. For example, $35.02$; $100.7$; $123\456.5$; $54.89$.
Decimal definition
Definition 1
Decimals-- these are fractional numbers that are represented in decimal notation.
For example, $121.05; $67.9$; $345.6700$.
Decimals are used to more compactly write proper fractions, the denominators of which are the numbers $10$, $100$, $1\000$, etc. and mixed numbers, the denominators of the fractional part of which are the numbers $10$, $100$, $1\000$, etc.
For example, the common fraction $\frac(8)(10)$ can be written as a decimal $0.8$, and the mixed number $405\frac(8)(100)$ can be written as a decimal $405.08$.
Reading Decimals
Decimals, which correspond to regular fractions, are read in the same way as ordinary fractions, only the phrase “zero integers” is added in front. For example, the common fraction $\frac(25)(100)$ (read “twenty-five hundredths”) corresponds to the decimal fraction $0.25$ (read “zero point twenty-five hundredths”).
Decimal fractions that correspond to mixed numbers are read the same way as mixed numbers. For example, the mixed number $43\frac(15)(1000)$ corresponds to the decimal fraction $43.015$ (read “forty-three point fifteen thousandths”).
Places in decimals
In writing a decimal fraction, the meaning of each digit depends on its position. Those. in decimal fractions the concept also applies category.
Places in decimal fractions up to the decimal point are called the same as places in natural numbers. The decimal places after the decimal point are listed in the table:
Picture 1.
Example 3
For example, in the decimal fraction $56.328$, the digit $5$ is in the tens place, $6$ is in the units place, $3$ is in the tenths place, $2$ is in the hundredths place, $8$ is in the thousandths place.
Places in decimal fractions are distinguished by precedence. When reading a decimal fraction, move from left to right - from senior rank to younger.
Example 4
For example, in the decimal fraction $56.328$, the most significant (highest) place is the tens place, and the low (lowest) place is the thousandths place.
A decimal fraction can be expanded into digits similar to the digit decomposition of a natural number.
Example 5
For example, let's break down the decimal fraction $37.851$ into digits:
$37,851=30+7+0,8+0,05+0,001$
Ending decimals
Definition 2
Ending decimals are called decimal fractions, the records of which contain a finite number of characters (digits).
For example, $0.138$; $5.34$; $56.123456$; $350,972.54.
Any finite decimal fraction can be converted to a fraction or a mixed number.
Example 6
For example, the final decimal fraction $7.39$ corresponds to the fractional number $7\frac(39)(100)$, and the final decimal fraction $0.5$ corresponds to the proper common fraction $\frac(5)(10)$ (or any fraction which is equal to it, for example, $\frac(1)(2)$ or $\frac(10)(20)$.
Converting a fraction to a decimal
Converting fractions with denominators $10, 100, \dots$ to decimals
Before converting some proper fractions to decimals, they must first be “prepared.” The result of such preparation should be the same number of digits in the numerator and the same number of zeros in the denominator.
The essence of “preliminary preparation” of proper ordinary fractions for conversion to decimal fractions is adding such a number of zeros to the left in the numerator that the total number of digits becomes equal to the number of zeros in the denominator.
Example 7
For example, let's prepare the fraction $\frac(43)(1000)$ for conversion to a decimal and get $\frac(043)(1000)$. And the ordinary fraction $\frac(83)(100)$ does not need any preparation.
Let's formulate rule for converting a proper common fraction with a denominator of $10$, or $100$, or $1\000$, $\dots$ into a decimal fraction:
write $0$;
after it put a decimal point;
write down the number from the numerator (along with added zeros after preparation, if necessary).
Example 8
Convert the proper fraction $\frac(23)(100)$ to a decimal.
Solution.
The denominator contains the number $100$, which contains $2$ and two zeros. The numerator contains the number $23$, which is written with $2$.digits. This means that there is no need to prepare this fraction for conversion to a decimal.
Let's write $0$, put a decimal point and write down the number $23$ from the numerator. We get the decimal fraction $0.23$.
Answer: $0,23$.
Example 9
Write the proper fraction $\frac(351)(100000)$ as a decimal.
Solution.
The numerator of this fraction contains $3$ digits, and the number of zeros in the denominator is $5$, so this ordinary fraction must be prepared for conversion to a decimal. To do this, you need to add $5-3=2$ zeros to the left in the numerator: $\frac(00351)(100000)$.
Now we can form the desired decimal fraction. To do this, write down $0$, then add a comma and write down the number from the numerator. We get the decimal fraction $0.00351$.
Answer: $0,00351$.
Let's formulate rule for converting improper fractions with denominators $10$, $100$, $\dots$ into decimal fractions:
write down the number from the numerator;
Use a decimal point to separate as many digits on the right as there are zeros in the denominator of the original fraction.
Example 10
Convert the improper fraction $\frac(12756)(100)$ to a decimal.
Solution.
Let's write down the number from the numerator $12756$, then separate the $2$ digits on the right with a decimal point, because the denominator of the original fraction $2$ is zero. We get the decimal fraction $127.56$.
In this article we will understand what a decimal fraction is, what features and properties it has. Go! 🙂
A decimal fraction is a special case of ordinary fractions (where the denominator is a multiple of 10).
Definition
Decimals are fractions whose denominators are numbers consisting of one and a number of zeros following it. That is, these are fractions with a denominator of 10, 100, 1000, etc. Otherwise, a decimal fraction can be characterized as a fraction with a denominator of 10 or one of the powers of ten.
Examples of fractions:
, ,
Decimal fractions are written differently than ordinary fractions. Operations with these fractions are also different from operations with ordinary ones. The rules for operations with them are largely similar to the rules for operations with integers. This, in particular, explains their demand for solving practical problems.
Representation of fractions in decimal notation
The decimal fraction does not have a denominator; it displays the number of the numerator. In general, a decimal fraction is written according to the following scheme:
where X is the integer part of the fraction, Y is its fractional part, “,” is the decimal point.
To correctly represent a fraction as a decimal, it requires that it be a regular fraction, that is, with the integer part highlighted (if possible) and a numerator that is less than the denominator. Then in decimal notation the integer part is written before the decimal point (X), and the numerator of the common fraction is written after the decimal point (Y).
If the numerator contains a number with fewer digits than the number of zeros in the denominator, then in part Y the missing number of digits in the decimal notation is filled with zeros ahead of the numerator digits.
Example: ![]()
If a common fraction is less than 1, i.e. does not have an integer part, then for X in decimal form write 0.
In the fractional part (Y), after the last significant (non-zero) digit, an arbitrary number of zeros can be entered. This does not affect the value of the fraction. Conversely, all zeros at the end of the fractional part of the decimal can be omitted.
Reading Decimals
Part X is generally read as follows: “X integers.”
The Y part is read according to the number in the denominator. For denominator 10 you should read: “Y tenths”, for denominator 100: “Y hundredths”, for denominator 1000: “Y thousandths” and so on... 😉
Another approach to reading, based on counting the number of digits of the fractional part, is considered more correct. To do this, you need to understand that the fractional digits are located in a mirror image with respect to the digits of the whole part of the fraction.
The names for correct reading are given in the table:

Based on this, reading should be based on compliance with the name of the digit of the last digit of the fractional part.
- 3.5 is read as "three point five"
- 0.016 reads "zero point sixteen thousandths"
Converting an arbitrary fraction to a decimal
If the denominator of a common fraction is 10 or some power of ten, then the conversion of the fraction is performed as described above. In other situations, additional transformations are required.
There are 2 translation methods.
First transfer method
The numerator and denominator must be multiplied by such an integer that the denominator produces the number 10 or one of the powers of ten. And then the fraction is represented in decimal notation.
This method is applicable for fractions whose denominator can only be expanded into 2 and 5. So, in the previous example ![]() . If the expansion contains other prime factors (for example, ), then you will have to resort to the 2nd method.
. If the expansion contains other prime factors (for example, ), then you will have to resort to the 2nd method.
Second translation method
The 2nd method is to divide the numerator by the denominator in a column or on a calculator. The whole part, if any, does not participate in the transformation.
The rule for long division that results in a decimal fraction is described below (see Division of decimals).
Converting a decimal fraction to a common fraction
To do this, you should write down its fractional part (to the right of the decimal point) as the numerator, and the result of reading the fractional part as the corresponding number in the denominator. Next, if possible, you need to reduce the resulting fraction.
![]()
Finite and infinite decimal fraction
A decimal fraction is called a final fraction, the fractional part of which consists of a finite number of digits.
All the examples above contain final decimal fractions. However, not every ordinary fraction can be represented as a final decimal. If the 1st conversion method is not applicable for a given fraction, and the 2nd method demonstrates that the division cannot be completed, then only an infinite decimal fraction can be obtained.
It is impossible to write an infinite fraction in its complete form. In incomplete form, such fractions can be represented:
- as a result of reduction to the desired number of decimal places;
- as a periodic fraction.
A fraction is called periodic if after the decimal point it is possible to distinguish an endlessly repeating sequence of digits.
The remaining fractions are called non-periodic. For non-periodic fractions, only the 1st method of representation (rounding) is allowed.
An example of a periodic fraction: 0.8888888... Here there is a repeating number 8, which, obviously, will be repeated ad infinitum, since there is no reason to assume otherwise. This figure is called period of the fraction.
Periodic fractions can be pure or mixed. A pure decimal fraction is one whose period begins immediately after the decimal point. A mixed fraction has 1 or more digits before the decimal point.
54.33333… – periodic pure decimal fraction
2.5621212121… – periodic mixed fraction
Examples of writing infinite decimal fractions:
The 2nd example shows how to correctly format a period in writing a periodic fraction.
Converting periodic decimal fractions to ordinary fractions
To convert a pure periodic fraction into an ordinary period, write it into the numerator, and write a number consisting of nines in an amount equal to the number of digits in the period into the denominator.
![]()
The mixed periodic decimal fraction is translated as follows:
- you need to form a number consisting of the number after the decimal point before the period and the first period;
- From the resulting number, subtract the number after the decimal point before the period. The result will be the numerator of the common fraction;
- in the denominator you need to enter a number consisting of a number of nines equal to the number of digits of the period, followed by zeros, the number of which is equal to the number of digits of the number after the decimal point before the 1st period.
![]()
![]()
Comparison of decimals
Decimal fractions are compared initially by their whole parts. The fraction whose whole part is larger is greater.
If the integer parts are the same, then compare the digits of the corresponding digits of the fractional part, starting from the first (from the tenths). The same principle applies here: the larger fraction is the one with more tenths; if the tenths digits are equal, the hundredths digits are compared, and so on.
Because the
![]() , since with equal whole parts and equal tenths in the fractional part, the 2nd fraction has a larger hundredths figure.
, since with equal whole parts and equal tenths in the fractional part, the 2nd fraction has a larger hundredths figure.
Adding and subtracting decimals
Decimals are added and subtracted in the same way as whole numbers by writing the corresponding digits below each other. To do this, you need to have decimal points below each other. Then the units (tens, etc.) of the integer part, as well as the tenths (hundredths, etc.) of the fractional part, will be in accordance. The missing digits of the fractional part are filled with zeros. Directly The process of addition and subtraction is carried out in the same way as for integers.
Multiplying Decimals
To multiply decimals, you need to write them one below the other, aligned with the last digit and not paying attention to the location of the decimal points. Then you need to multiply the numbers in the same way as when multiplying whole numbers. After receiving the result, you should recalculate the number of digits after the decimal point in both fractions and separate the total number of fractional digits in the resulting number with a comma. If there are not enough digits, they are replaced with zeros.

Multiplying and dividing decimals by 10n
These actions are simple and boil down to moving the decimal point. P When multiplying, the decimal point is moved to the right (the fraction is increased) by a number of digits equal to the number of zeros in 10n, where n is an arbitrary integer power. That is, a certain number of digits are transferred from the fractional part to the whole part. When dividing, accordingly, the comma is moved to the left (the number decreases), and some of the digits are transferred from the integer part to the fractional part. If there are not enough numbers to transfer, then the missing bits are filled with zeros.
This article is about decimals. Here we will understand the decimal notation of fractional numbers, introduce the concept of a decimal fraction and give examples of decimal fractions. Next we’ll talk about the digits of decimal fractions and give the names of the digits. After this, we will focus on infinite decimal fractions, let's talk about periodic and non-periodic fractions. Next we list the basic operations with decimal fractions. In conclusion, let us establish the position of decimal fractions on the coordinate beam.
Page navigation.
Decimal notation of a fractional number
Reading Decimals
Let's say a few words about the rules for reading decimal fractions.
Decimal fractions, which correspond to proper ordinary fractions, are read in the same way as these ordinary fractions, only “zero integer” is first added. For example, the decimal fraction 0.12 corresponds to the common fraction 12/100 (read “twelve hundredths”), therefore, 0.12 is read as “zero point twelve hundredths”.
Decimal fractions that correspond to mixed numbers are read exactly the same as these mixed numbers. For example, the decimal fraction 56.002 corresponds to a mixed number, so the decimal fraction 56.002 is read as “fifty-six point two thousandths.”
Places in decimals
In writing decimal fractions, as well as in writing natural numbers, the meaning of each digit depends on its position. Indeed, the number 3 in the decimal fraction 0.3 means three tenths, in the decimal fraction 0.0003 - three ten thousandths, and in the decimal fraction 30,000.152 - three tens of thousands. So we can talk about decimal places, as well as about the digits in natural numbers.
The names of the digits in the decimal fraction up to the decimal point completely coincide with the names of the digits in natural numbers. And the names of the decimal places after the decimal point can be seen from the following table.

For example, in the decimal fraction 37.051, the digit 3 is in the tens place, 7 is in the units place, 0 is in the tenths place, 5 is in the hundredths place, and 1 is in the thousandths place.
Places in decimal fractions also differ in precedence. If in writing a decimal fraction we move from digit to digit from left to right, then we will move from seniors To junior ranks. For example, the hundreds place is older than the tenths place, and the millions place is lower than the hundredths place. In a given final decimal fraction, we can talk about the major and minor digits. For example, in decimal fraction 604.9387 senior (highest) the place is the hundreds place, and junior (lowest)- ten-thousandths digit.
For decimal fractions, expansion into digits takes place. It is similar to expansion into digits of natural numbers. For example, the expansion into decimal places of 45.6072 is as follows: 45.6072=40+5+0.6+0.007+0.0002. And the properties of addition from the decomposition of a decimal fraction into digits allow you to move on to other representations of this decimal fraction, for example, 45.6072=45+0.6072, or 45.6072=40.6+5.007+0.0002, or 45.6072= 45.0072+0.6.
Ending decimals
Up to this point, we have only talked about decimal fractions, in the notation of which there is a finite number of digits after the decimal point. Such fractions are called finite decimals.
Definition.
Ending decimals- These are decimal fractions, the records of which contain a finite number of characters (digits).
Here are some examples of final decimal fractions: 0.317, 3.5, 51.1020304958, 230,032.45.
However, not every fraction can be represented as a final decimal. For example, the fraction 5/13 cannot be replaced by an equal fraction with one of the denominators 10, 100, ..., therefore, cannot be converted into a final decimal fraction. We will talk more about this in the theory section, converting ordinary fractions to decimals.
Infinite Decimals: Periodic Fractions and Non-Periodic Fractions
In writing a decimal fraction after the decimal point, you can assume the possibility of an infinite number of digits. In this case, we will come to consider the so-called infinite decimal fractions.
Definition.
Infinite decimals- These are decimal fractions, which contain an infinite number of digits.
It is clear that we cannot write down infinite decimal fractions in full form, so in their recording we limit ourselves to only a certain finite number of digits after the decimal point and put an ellipsis indicating an infinitely continuing sequence of digits. Here are some examples of infinite decimal fractions: 0.143940932…, 3.1415935432…, 153.02003004005…, 2.111111111…, 69.74152152152….
If you look closely at the last two infinite decimal fractions, then in the fraction 2.111111111... the endlessly repeating number 1 is clearly visible, and in the fraction 69.74152152152..., starting from the third decimal place, a repeating group of numbers 1, 5 and 2 is clearly visible. Such infinite decimal fractions are called periodic.
Definition.
Periodic decimals(or simply periodic fractions) are endless decimal fractions, in the recording of which, starting from a certain decimal place, some number or group of numbers is endlessly repeated, which is called period of the fraction.
For example, the period of the periodic fraction 2.111111111... is the digit 1, and the period of the fraction 69.74152152152... is a group of digits of the form 152.
For infinite periodic decimal fractions, a special form of notation is adopted. For brevity, we agreed to write down the period once, enclosing it in parentheses. For example, the periodic fraction 2.111111111... is written as 2,(1) , and the periodic fraction 69.74152152152... is written as 69.74(152) .
It is worth noting that different periods can be specified for the same periodic decimal fraction. For example, the periodic decimal fraction 0.73333... can be considered as a fraction 0.7(3) with a period of 3, and also as a fraction 0.7(33) with a period of 33, and so on 0.7(333), 0.7 (3333), ... You can also look at the periodic fraction 0.73333 ... like this: 0.733(3), or like this 0.73(333), etc. Here, in order to avoid ambiguity and discrepancies, we agree to consider as the period of a decimal fraction the shortest of all possible sequences of repeating digits, and starting from the closest position to the decimal point. That is, the period of the decimal fraction 0.73333... will be considered a sequence of one digit 3, and the periodicity starts from the second position after the decimal point, that is, 0.73333...=0.7(3). Another example: the periodic fraction 4.7412121212... has a period of 12, the periodicity starts from the third digit after the decimal point, that is, 4.7412121212...=4.74(12).
Infinite decimal periodic fractions are obtained by converting into decimal fractions ordinary fractions whose denominators contain prime factors other than 2 and 5.
Here it is worth mentioning periodic fractions with a period of 9. Let us give examples of such fractions: 6.43(9) , 27,(9) . These fractions are another notation for periodic fractions with period 0, and they are usually replaced by periodic fractions with period 0. To do this, period 9 is replaced by period 0, and the value of the next highest digit is increased by one. For example, a fraction with period 9 of the form 7.24(9) is replaced by a periodic fraction with period 0 of the form 7.25(0) or an equal final decimal fraction 7.25. Another example: 4,(9)=5,(0)=5. The equality of a fraction with period 9 and its corresponding fraction with period 0 is easily established after replacing these decimal fractions with equal ordinary fractions.
Finally, let's take a closer look at infinite decimal fractions, which do not contain an endlessly repeating sequence of digits. They are called non-periodic.
Definition.
Non-recurring decimals(or simply non-periodic fractions) are infinite decimal fractions that have no period.
Sometimes non-periodic fractions have a form similar to that of periodic fractions, for example, 8.02002000200002... is a non-periodic fraction. In these cases, you should be especially careful to notice the difference.
Note that non-periodic fractions do not convert to ordinary fractions; infinite non-periodic decimal fractions represent irrational numbers.
Operations with decimals
One of the operations with decimal fractions is comparison, and the four basic arithmetic functions are also defined operations with decimals: addition, subtraction, multiplication and division. Let's consider separately each of the actions with decimal fractions.
Comparison of decimals essentially based on comparison of ordinary fractions corresponding to the decimal fractions being compared. However, converting decimal fractions into ordinary fractions is a rather labor-intensive process, and infinite non-periodic fractions cannot be represented as an ordinary fraction, so it is convenient to use a place-wise comparison of decimal fractions. Place-wise comparison of decimal fractions is similar to comparison of natural numbers. For more detailed information, we recommend studying the article: comparison of decimal fractions, rules, examples, solutions.
Let's move on to the next step - multiplying decimals. Multiplication of finite decimal fractions is carried out similarly to subtraction of decimal fractions, rules, examples, solutions to multiplication by a column of natural numbers. In the case of periodic fractions, multiplication can be reduced to multiplication of ordinary fractions. In turn, the multiplication of infinite non-periodic decimal fractions after their rounding is reduced to the multiplication of finite decimal fractions. We recommend for further study the material in the article: multiplication of decimal fractions, rules, examples, solutions.
Decimals on a coordinate ray
There is a one-to-one correspondence between points and decimals.
Let's figure out how points on the coordinate ray are constructed that correspond to a given decimal fraction.
We can replace finite decimal fractions and infinite periodic decimal fractions with equal ordinary fractions, and then construct the corresponding ordinary fractions on the coordinate ray. For example, the decimal fraction 1.4 corresponds to the common fraction 14/10, so the point with coordinate 1.4 is removed from the origin in the positive direction by 14 segments equal to a tenth of a unit segment.

Decimal fractions can be marked on a coordinate ray, starting from the decomposition of a given decimal fraction into digits. For example, let us need to build a point with coordinate 16.3007, since 16.3007=16+0.3+0.0007, then we can get to this point by sequentially laying 16 unit segments from the origin of coordinates, 3 segments whose length equal to a tenth of a unit, and 7 segments, the length of which is equal to a ten-thousandth of a unit segment.
This method of constructing decimal numbers on a coordinate ray allows you to get as close as you like to the point corresponding to an infinite decimal fraction.
Sometimes it is possible to accurately plot the point corresponding to an infinite decimal fraction. For example, ![]() , then this infinite decimal fraction 1.41421... corresponds to a point on the coordinate ray, distant from the origin of coordinates by the length of the diagonal of a square with a side of 1 unit segment.
, then this infinite decimal fraction 1.41421... corresponds to a point on the coordinate ray, distant from the origin of coordinates by the length of the diagonal of a square with a side of 1 unit segment.
The reverse process of obtaining the decimal fraction corresponding to a given point on a coordinate ray is the so-called decimal measurement of a segment. Let's figure out how it is done.
Let our task be to get from the origin to a given point on the coordinate line (or to infinitely approach it if we can’t get to it). With the decimal measurement of a segment, we can sequentially lay off from the origin any number of unit segments, then segments whose length is equal to a tenth of a unit, then segments whose length is equal to a hundredth of a unit, etc. By recording the number of segments of each length laid aside, we obtain the decimal fraction corresponding to a given point on the coordinate ray.
For example, to get to point M in the above figure, you need to set aside 1 unit segment and 4 segments, the length of which is equal to a tenth of a unit. Thus, point M corresponds to the decimal fraction 1.4.
It is clear that the points of the coordinate ray, which cannot be reached in the process of decimal measurement, correspond to infinite decimal fractions.
Bibliography.
- Mathematics: textbook for 5th grade. general education institutions / N. Ya. Vilenkin, V. I. Zhokhov, A. S. Chesnokov, S. I. Shvartsburd. - 21st ed., erased. - M.: Mnemosyne, 2007. - 280 pp.: ill. ISBN 5-346-00699-0.
- Mathematics. 6th grade: educational. for general education institutions / [N. Ya. Vilenkin and others]. - 22nd ed., rev. - M.: Mnemosyne, 2008. - 288 p.: ill. ISBN 978-5-346-00897-2.
- Algebra: textbook for 8th grade. general education institutions / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; edited by S. A. Telyakovsky. - 16th ed. - M.: Education, 2008. - 271 p. : ill. - ISBN 978-5-09-019243-9.
- Gusev V. A., Mordkovich A. G. Mathematics (a manual for those entering technical schools): Proc. allowance.- M.; Higher school, 1984.-351 p., ill.
Fractions
Attention!
There are additional
materials in Special Section 555.
For those who are very "not very..."
And for those who “very much…”)
Fractions are not much of a nuisance in high school. For the time being. Until you come across powers with rational exponents and logarithms. And there... You press and press the calculator, and it shows a full display of some numbers. You have to think with your head like in the third grade.
Let's finally figure out fractions! Well, how much can you get confused in them!? Moreover, it’s all simple and logical. So, what are the types of fractions?
Types of fractions. Transformations.
There are three types of fractions.
1. Common fractions , For example:
Sometimes instead of a horizontal line they put a slash: 1/2, 3/4, 19/5, well, and so on. Here we will often use this spelling. The top number is called numerator, lower - denominator. If you constantly confuse these names (it happens...), say to yourself the phrase: " Zzzzz remember! Zzzzz denominator - look zzzzz uh!" Look, everything will be zzzz remembered.)
The dash, either horizontal or inclined, means division the top number (numerator) to the bottom (denominator). That's all! Instead of a dash, it is quite possible to put a division sign - two dots.
When complete division is possible, this must be done. So, instead of the fraction “32/8” it is much more pleasant to write the number “4”. Those. 32 is simply divided by 8.
32/8 = 32: 8 = 4
I'm not even talking about the fraction "4/1". Which is also just "4". And if it’s not completely divisible, we leave it as a fraction. Sometimes you have to do the opposite operation. Convert a whole number into a fraction. But more on that later.
2. Decimals , For example:
It is in this form that you will need to write down the answers to tasks “B”.
3. Mixed numbers , For example:
Mixed numbers are practically not used in high school. In order to work with them, they must be converted into ordinary fractions. But you definitely need to be able to do this! Otherwise you will come across such a number in a problem and freeze... Out of nowhere. But we will remember this procedure! A little lower.
Most versatile common fractions. Let's start with them. By the way, if a fraction contains all sorts of logarithms, sines and other letters, this does not change anything. In the sense that everything actions with fractional expressions are no different from actions with ordinary fractions!
The main property of a fraction.
So, let's go! To begin with, I will surprise you. The whole variety of fraction transformations is provided by one single property! That's what it's called main property of a fraction. Remember: If the numerator and denominator of a fraction are multiplied (divided) by the same number, the fraction does not change. Those:
It is clear that you can continue to write until you are blue in the face. Don’t let sines and logarithms confuse you, we’ll deal with them further. The main thing is to understand that all these various expressions are the same fraction . 2/3.
Do we need it, all these transformations? And how! Now you will see for yourself. To begin with, let's use the basic property of a fraction for reducing fractions. It would seem like an elementary thing. Divide the numerator and denominator by the same number and that's it! It's impossible to make a mistake! But... man is a creative being. You can make a mistake anywhere! Especially if you have to reduce not a fraction like 5/10, but a fractional expression with all sorts of letters.
How to correctly and quickly reduce fractions without doing extra work can be read in the special Section 555.
A normal student doesn't bother dividing the numerator and denominator by the same number (or expression)! He simply crosses out everything that is the same above and below! This is where a typical mistake, a blunder, if you will, lurks.
For example, you need to simplify the expression:
There’s nothing to think about here, cross out the letter “a” on top and the two on the bottom! We get:
Everything is correct. But really you divided all numerator and all the denominator is "a". If you are used to just crossing out, then in a hurry you can cross out the “a” in the expression
and get it again
Which would be categorically untrue. Because here all the numerator on "a" is already not shared! This fraction cannot be reduced. By the way, such a reduction is, um... a serious challenge for the teacher. This is not forgiven! Do you remember? When reducing, you need to divide all numerator and all denominator!
Reducing fractions makes life a lot easier. You will get a fraction somewhere, for example 375/1000. How can I continue to work with her now? Without a calculator? Multiply, say, add, square!? And if you’re not too lazy, and carefully cut it down by five, and by another five, and even... while it’s being shortened, in short. Let's get 3/8! Much nicer, right?
The main property of a fraction allows you to convert ordinary fractions to decimals and vice versa without a calculator! This is important for the Unified State Exam, right?
How to convert fractions from one type to another.
With decimal fractions everything is simple. As it is heard, so it is written! Let's say 0.25. This is zero point twenty five hundredths. So we write: 25/100. We reduce (we divide the numerator and denominator by 25), we get the usual fraction: 1/4. All. It happens, and nothing is reduced. Like 0.3. This is three tenths, i.e. 3/10.
What if the integers are not zero? It's OK. We write down the whole fraction without any commas in the numerator, and in the denominator - what is heard. For example: 3.17. This is three point seventeen hundredths. We write 317 in the numerator and 100 in the denominator. We get 317/100. Nothing is reduced, that means everything. This is the answer. Elementary Watson! From all that has been said, a useful conclusion: any decimal fraction can be converted to a common fraction .
But some people cannot do the reverse conversion from ordinary to decimal without a calculator. And it is necessary! How will you write down the answer on the Unified State Exam!? Read carefully and master this process.
What is the characteristic of a decimal fraction? Her denominator is Always costs 10, or 100, or 1000, or 10000 and so on. If your common fraction has a denominator like this, there's no problem. For example, 4/10 = 0.4. Or 7/100 = 0.07. Or 12/10 = 1.2. What if the answer to the task in section “B” turned out to be 1/2? What will we write in response? Decimals are required...
Let's remember main property of a fraction ! Mathematics favorably allows you to multiply the numerator and denominator by the same number. Anything, by the way! Except zero, of course. So let’s use this property to our advantage! What can the denominator be multiplied by, i.e. 2 so that it becomes 10, or 100, or 1000 (smaller is better, of course...)? At 5, obviously. Feel free to multiply the denominator (this is us necessary) by 5. But then the numerator must also be multiplied by 5. This is already mathematics demands! We get 1/2 = 1x5/2x5 = 5/10 = 0.5. That's all.
However, all sorts of denominators come across. You will come across, for example, the fraction 3/16. Try and figure out what to multiply 16 by to make 100, or 1000... Doesn’t it work? Then you can simply divide 3 by 16. In the absence of a calculator, you will have to divide with a corner, on a piece of paper, as they taught in elementary school. We get 0.1875.
And there are also very bad denominators. For example, there is no way to turn the fraction 1/3 into a good decimal. Both on the calculator and on a piece of paper, we get 0.3333333... This means that 1/3 is an exact decimal fraction does not translate. Same as 1/7, 5/6 and so on. There are many of them, untranslatable. This brings us to another useful conclusion. Not every fraction can be converted to a decimal !
By the way, this is useful information for self-testing. In section "B" you must write down a decimal fraction in your answer. And you got, for example, 4/3. This fraction does not convert to a decimal. This means you made a mistake somewhere along the way! Go back and check the solution.
So, we figured out ordinary and decimal fractions. All that remains is to deal with mixed numbers. To work with them, they must be converted into ordinary fractions. How to do it? You can catch a sixth grader and ask him. But a sixth grader won’t always be at hand... You’ll have to do it yourself. It is not difficult. You need to multiply the denominator of the fractional part by the whole part and add the numerator of the fractional part. This will be the numerator of the common fraction. What about the denominator? The denominator will remain the same. It sounds complicated, but in reality everything is simple. Let's look at an example.
Suppose you were horrified to see the number in the problem:
Calmly, without panic, we think. The whole part is 1. Unit. The fractional part is 3/7. Therefore, the denominator of the fractional part is 7. This denominator will be the denominator of the ordinary fraction. We count the numerator. We multiply 7 by 1 (the integer part) and add 3 (the numerator of the fractional part). We get 10. This will be the numerator of a common fraction. That's all. It looks even simpler in mathematical notation:

Is it clear? Then secure your success! Convert to ordinary fractions. You should get 10/7, 7/2, 23/10 and 21/4.
The reverse operation - converting an improper fraction to a mixed number - is rarely required in high school. Well, if so... And if you are not in high school, you can look into the special Section 555. By the way, you will also learn about improper fractions there.
Well, that's practically all. You remembered the types of fractions and understood How transfer them from one type to another. The question remains: For what do it? Where and when to apply this deep knowledge?
I answer. Any example itself suggests the necessary actions. If in the example ordinary fractions, decimals, and even mixed numbers are mixed together, we convert everything into ordinary fractions. It can always be done. Well, if it says something like 0.8 + 0.3, then we count it that way, without any translation. Why do we need extra work? We choose the solution that is convenient us !
If the task is all decimal fractions, but um... some kind of evil ones, go to ordinary ones, try it! Look, everything will work out. For example, you will have to square the number 0.125. It’s not so easy if you haven’t gotten used to using a calculator! Not only do you have to multiply numbers in a column, you also have to think about where to insert the comma! It definitely won’t work in your head! What if we move on to an ordinary fraction?
0.125 = 125/1000. We reduce it by 5 (this is for starters). We get 25/200. Once again by 5. We get 5/40. Oh, it's still shrinking! Back to 5! We get 1/8. We easily square it (in our minds!) and get 1/64. All!
Let's summarize this lesson.
1. There are three types of fractions. Common, decimal and mixed numbers.
2. Decimals and mixed numbers Always can be converted to ordinary fractions. Reverse transfer not always available.
3. The choice of the type of fractions to work with a task depends on the task itself. If there are different types of fractions in one task, the most reliable thing is to switch to ordinary fractions.
Now you can practice. First, convert these decimal fractions to ordinary fractions:
3,8; 0,75; 0,15; 1,4; 0,725; 0,012
You should get answers like this (in a mess!):
Let's wrap this up. In this lesson we refreshed our memory on key points about fractions. It happens, however, that there is nothing special to refresh...) If someone has completely forgotten, or has not yet mastered it... Then you can go to a special Section 555. All the basics are covered in detail there. Many suddenly understand everything are starting. And they solve fractions on the fly).
If you like this site...
By the way, I have a couple more interesting sites for you.)
You can practice solving examples and find out your level. Testing with instant verification. Let's learn - with interest!)
You can get acquainted with functions and derivatives.