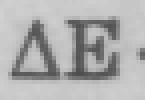Definition and properties. Definition and properties of Expressions using complex numbers

Real logarithm

Logarithm of a real number log a b makes sense with style="max-width: 98%; height: auto; width: auto;" src="/pictures/wiki/files/55/7cd1159e49fee8eff61027c9cde84a53.png" border="0">.

The most widely used types of logarithms are:

If we consider the logarithmic number as a variable, we get logarithmic function, For example: . This function is defined on the right side of the number line: x> 0, is continuous and differentiable there (see Fig. 1).

Properties

Natural logarithms

When the equality is true

(1)

In particular,

This series converges faster, and in addition, the left side of the formula can now express the logarithm of any positive number.

Relationship with the decimal logarithm: .

Decimal logarithms

Rice. 2. Logarithmic scale

Logarithms to base 10 (symbol: lg a) before the invention of calculators were widely used for calculations. The uneven scale of decimal logarithms is usually marked on slide rules as well. A similar scale is widely used in various fields of science, for example:

Chemistry - activity of hydrogen ions ().
Music theory - note scale, in relation to the frequencies of musical notes.

The logarithmic scale is also widely used to identify the exponent in power relations and the coefficient in the exponent. In this case, a graph constructed on a logarithmic scale along one or two axes takes the form of a straight line, which is easier to study.

Complex logarithm

Multivalued function

Riemann surface

A complex logarithmic function is an example of a Riemann surface; its imaginary part (Fig. 3) consists of an infinite number of branches, twisted like a spiral. This surface is simply connected; its only zero (of first order) is obtained at z= 1, singular points: z= 0 and (branch points of infinite order).

The Riemann surface of the logarithm is the universal covering for the complex plane without the point 0.

Historical sketch

Real logarithm

The need for complex calculations grew rapidly in the 16th century, and much of the difficulty involved multiplying and dividing multi-digit numbers. At the end of the century, several mathematicians, almost simultaneously, came up with the idea: to replace labor-intensive multiplication with simple addition, using special tables to compare the geometric and arithmetic progressions, with the geometric one being the original one. Then division is automatically replaced by the immeasurably simpler and more reliable subtraction. He was the first to publish this idea in his book “ Arithmetica integra"Michael Stiefel, who, however, did not make serious efforts to implement his idea.

In the 1620s, Edmund Wingate and William Oughtred invented the first slide rule, before the advent of pocket calculators—an indispensable engineer's tool.

A close to modern understanding of logarithmation - as the inverse operation of raising to a power - first appeared with Wallis and Johann Bernoulli, and was finally legitimized by Euler in the 18th century. In the book “Introduction to the Analysis of Infinite” (), Euler gave modern definitions of both exponential and logarithmic functions, expanded them into power series, and especially noted the role of the natural logarithm.

Euler is also credited with extending the logarithmic function to the complex domain.

Complex logarithm

Although the dispute continued (D'Alembert defended his point of view and argued it in detail in an article in his Encyclopedia and in other works), Euler's point of view quickly gained universal recognition.

Logarithmic tables

From the properties of the logarithm it follows that instead of labor-intensive multiplication of multi-digit numbers, it is enough to find (from tables) and add their logarithms, and then, using the same tables, perform potentiation, that is, find the value of the result from its logarithm. Doing division differs only in that logarithms are subtracted. Laplace said that the invention of logarithms “extended the life of astronomers” by greatly speeding up the process of calculations.

When moving the decimal point in a number to n digits, the value of the decimal logarithm of this number changes to n. For example, log8314.63 = log8.31463 + 3. It follows that it is enough to compile a table of decimal logarithms for numbers in the range from 1 to 10.

The first tables of logarithms were published by John Napier (), and they contained only logarithms of trigonometric functions, and with errors. Independently of him, Joost Bürgi, a friend of Kepler (), published his tables. In 1617, Oxford mathematics professor Henry Briggs published tables that already included decimal logarithms of the numbers themselves, from 1 to 1000, with 8 (later 14) digits. But there were also errors in Briggs’ tables. The first error-free edition based on the Vega tables () appeared only in 1857 in Berlin (Bremiwer tables).

In Russia, the first tables of logarithms were published in 1703 with the participation of L. F. Magnitsky. Several collections of logarithm tables were published in the USSR.

Bradis V. M. Four-digit math tables. 44th edition, M., 1973.

The exponential function of a real variable (with a positive base) is determined in several steps. First, for natural values - as a product of equal factors. The definition then extends to negative integers and non-zero values for by the rules. Next, we consider fractional exponents, in which the value of the exponential function is determined using roots: . For irrational values, the definition is already connected with the basic concept of mathematical analysis - with the passage to the limit, for reasons of continuity. All these considerations are in no way applicable to attempts to extend the exponential function to complex values of the indicator, and what it is, for example, is completely unclear.

For the first time, a power with a complex exponent with a natural base was introduced by Euler based on an analysis of a number of constructions of integral calculus. Sometimes very similar algebraic expressions, when integrated, give completely different answers:

At the same time, here the second integral is formally obtained from the first when replaced by

From this we can conclude that with the proper definition of an exponential function with a complex exponent, inverse trigonometric functions are related to logarithms and thus the exponential function is related to trigonometric ones.

Euler had the courage and imagination to give a reasonable definition for an exponential function with a base, namely,

This is a definition, and therefore this formula cannot be proven; one can only look for arguments in favor of the reasonableness and expediency of such a definition. Mathematical analysis provides many arguments of this kind. We will limit ourselves to just one.

It is known that for real there is a limiting relation: . On the right side there is a polynomial that also makes sense for complex values for . The limit of a sequence of complex numbers is determined naturally. A sequence is considered convergent if the sequences of real and imaginary parts converge and is accepted

Let's find it. To do this, let's turn to the trigonometric form and for the argument we will select values from the interval. With this choice it is clear that for . Further,

To go to the limit, you need to verify the existence of limits for and and find these limits. It is clear that

So, in the expression

the real part tends to , the imaginary part tends to so

This simple reasoning provides one of the arguments in favor of Euler's definition of the exponential function.

Let us now establish that when multiplying the values of an exponential function, the exponents add up. Really:

2. Euler's formulas.

Let us put in the definition of the exponential function . We get:

Replacing b with -b, we get

By adding and subtracting these equalities term by term, we find the formulas

called Euler's formulas. They establish a connection between trigonometric functions and exponential functions with imaginary exponents.

3. Natural logarithm of a complex number.

A complex number given in trigonometric form can be written in the form. This form of writing a complex number is called exponential. It retains all the good properties of trigonometric form, but is even more concise. Further, Therefore, it is natural to assume that the real part of the logarithm of a complex number is the logarithm of its modulus, and the imaginary part is its argument. This to some extent explains the “logarithmic” property of the argument - the argument of the product is equal to the sum of the arguments of the factors.

At the same time, here the second integral is formally obtained from the first when replaced by

Euler had the courage and imagination to give a reasonable definition for an exponential function with a base, namely,

Let's find it. To do this, let's turn to the trigonometric form and for the argument we will select values from the interval. With this choice it is clear that for . Further,

To go to the limit, you need to verify the existence of limits for and and find these limits. It is clear that

So, in the expression

the real part tends to , the imaginary part tends to so

This simple reasoning provides one of the arguments in favor of Euler's definition of the exponential function.

Let us now establish that when multiplying the values of an exponential function, the exponents add up. Really:

2. Euler's formulas.

Let us put in the definition of the exponential function . We get:

Replacing b with -b, we get

By adding and subtracting these equalities term by term, we find the formulas

called Euler's formulas. They establish a connection between trigonometric functions and exponential functions with imaginary exponents.

3. Natural logarithm of a complex number.

Plan:

1 Real logarithm
- 1.1 Properties
- 1.2 Logarithmic function
- 1.3 Natural logarithms
- 1.4 Decimal logarithms
2 Complex logarithm
- 2.1 Definition and properties
- 2.2 Examples
- 2.3 Analytical continuation
- 2.4 Riemann surface
3 Historical sketch
- 3.1 Real logarithm
- 3.2 Complex logarithm
4 Logarithmic tables
5 Applications

Introduction

Rice. 1. Graphs of logarithmic functions

Logarithm of a number b based on a (from Greek λόγος - “word”, “attitude” and ἀριθμός - “number”) is defined as an indicator of the power to which the base must be raised a to get the number b. Designation: . From the definition it follows that the records and are equivalent.

For example, because.

1. Real logarithm

Logarithm of a real number log a b makes sense when . As is known, the exponential function y = a x is monotonic and each value takes only once, and the range of its values contains all positive real numbers. It follows that the value of the real logarithm of a positive number always exists and is uniquely determined.

The most widely used types of logarithms are:

1.1. Properties

Proof

Let's prove that .

(since by condition bc > 0). ■

Proof

Let's prove that

(since by condition ■

Proof

We use the identity to prove it. Let's logarithm both sides of the identity to base c. We get:

Proof

Let's prove that .

(because b p> 0 by condition). ■

Proof

Let's prove that

Proof

Logarithm the left and right sides to the base c :

Left side: Right side:

The equality of expressions is obvious. Since logarithms are equal, then, due to the monotonicity of the logarithmic function, the expressions themselves are equal. ■

1.2. Logarithmic function

If we consider the logarithmic number as a variable, we get logarithmic function y=log a x (see Fig. 1). It is defined at . Range of values: .

The function is strictly increasing at a> 1 and strictly decreasing at 0< a < 1 . График любой логарифмической функции проходит через точку (1;0) . Функция непрерывна и неограниченно дифференцируема всюду в своей области определения.

Straight x= 0 is a left vertical asymptote, since at a> 1 and at 0< a < 1 .

The derivative of the logarithmic function is equal to:

Proof

I. Let us prove that

Let's write down the identity e ln x = x and differentiate its left and right sides

We get that, from which it follows that

II. Let's prove that

The logarithmic function carries out an isomorphism between the multiplicative group of positive real numbers and the additive group of all real numbers.

1.3. Natural logarithms

Relationship with the decimal logarithm: .

As stated above, the derivative of the natural logarithm has a simple formula:

For this reason, natural logarithms are predominantly used in mathematical research. They often appear when solving differential equations, studying statistical dependencies (for example, the distribution of prime numbers), etc.

The indefinite integral of the natural logarithm can be easily found by integration by parts:

The Taylor series expansion can be represented as follows:
when the equality is true

(1)

In particular,

This series converges faster, and in addition, the left side of the formula can now express the logarithm of any positive number.

1.4. Decimal logarithms

Rice. 2a. Logarithmic scale

Rice. 2b. Logarithmic scale with symbols

Logarithms to base 10 (symbol: lg a) before the invention of calculators were widely used for calculations. The uneven scale of decimal logarithms is usually applied to slide rules. A similar scale is used in many fields of science, for example:

Physics - sound intensity (decibels).
Astronomy - star brightness scale.
Chemistry - hydrogen ion activity (pH).
Seismology - Richter scale.
Music theory - note scale, in relation to the frequencies of musical notes.
History is a logarithmic time scale.

2. Complex logarithm

2.1. Definition and properties

For complex numbers, the logarithm is defined in the same way as a real one. In practice, the natural complex logarithm is used almost exclusively, which we denote and define as the set of all complex numbers z such that e z = w . The complex logarithm exists for any , and its real part is determined uniquely, while the imaginary part has an infinite number of values. For this reason, it is called a multi-valued function. If you imagine w in demonstrative form:

then the logarithm is found by the formula:

Here is the real logarithm, r = | w | , k- arbitrary integer. The value obtained when k= 0, called main importance complex natural logarithm; it is customary to take the value of the argument in it in the interval (− π,π]. The corresponding (already single-valued) function is called main branch logarithm and is denoted by . Sometimes through also denotes a logarithm value that does not lie on the main branch.

From the formula it follows:

The real part of the logarithm is determined by the formula:

The logarithm of a negative number is found by the formula:

Since complex trigonometric functions are related to the exponent (Euler's formula), the complex logarithm, as the inverse function of the exponential, is related to the inverse trigonometric functions. An example of such a connection:

2.2. Examples

Let's give the main value of the logarithm for some arguments:

You should be careful when converting complex logarithms, taking into account that they are multi-valued, and therefore the equality of the logarithms of any expressions does not imply the equality of these expressions. Example of flawed reasoning:

iπ = ln(− 1) = ln((− i) 2) = 2ln(− i) = 2(− iπ / 2) = − iπ - sheer absurdity.

Note that on the left is the main value of the logarithm, and on the right is the value from the underlying branch ( k= − 1 ). The cause of the error is the careless use of the property, which, generally speaking, implies in the complex case the entire infinite set of logarithm values, and not just the main value.

2.3. Analytical continuation

Rice. 3. Complex logarithm (imaginary part)

The logarithm of a complex number can also be defined as the analytic extension of the real logarithm to the entire complex plane. Let the curve Γ begin at unity, not pass through zero, and not intersect the negative part of the real axis. Then the principal value of the logarithm at the end point w curve Γ can be determined by the formula:

If Γ is a simple curve (without self-intersections), then for the numbers lying on it, logarithmic identities can be applied without fear, for example

If the curve Γ is allowed to intersect the negative part of the real axis, then the first such intersection transfers the result from the principal value branch to the adjacent branch, and each subsequent intersection causes a similar shift along the branches of the logarithmic function (see figure).

From the analytic continuation formula it follows that on any branch of the logarithm

For any circle S, covering point 0:

The integral is taken in the positive direction (counterclockwise). This identity underlies the theory of residues.

You can also define the analytical continuation of the complex logarithm using the above series (1), generalized to the case of a complex argument. However, from the type of expansion it follows that at unity it is equal to zero, that is, the series relates only to the main branch of the multivalued function of the complex logarithm.

2.4. Riemann surface

A complex logarithmic function is an example of a Riemann surface; its imaginary part (Fig. 3) consists of an infinite number of branches twisted in the form of a spiral. This surface is simply connected; its only zero (of first order) is obtained at z= 1, singular points: z= 0 and (branch points of infinite order).

The Riemann surface of the logarithm is the universal covering for the complex plane without the point 0.

3. Historical sketch

3.1. Real logarithm

The need for complex calculations grew rapidly in the 16th century, and much of the difficulty involved multiplying and dividing multi-digit numbers and taking roots. At the end of the century, several mathematicians, almost simultaneously, came up with the idea: to replace labor-intensive multiplication with simple addition, using special tables to compare the geometric and arithmetic progressions, with the geometric one being the original one. Then division is automatically replaced by the immeasurably simpler and more reliable subtraction, and extracting the root of the degree n comes down to dividing the logarithm of the radical expression by n. He was the first to publish this idea in his book “ Arithmetica integra"Michael Stiefel, who, however, did not make any serious efforts to implement his idea.

In 1614, the Scottish amateur mathematician John Napier published an essay in Latin entitled " Description of the amazing table of logarithms"(lat. Mirifici Logarithmorum Canonis Descriptio ). It contained a brief description of logarithms and their properties, as well as 8-digit tables of logarithms of sines, cosines and tangents, with a step of 1". Term logarithm, proposed by Napier, has established itself in science. Napier outlined the theory of logarithms in his other book “ Building an Amazing Logarithm Table"(lat. Mirifici Logarithmorum Canonis Constructio ), published posthumously in 1619 by his son.

The concept of function did not yet exist, and Napier defined the logarithm kinematically, comparing uniform and logarithmically slow motion; for example, he defined the logarithm of sine as follows:

The logarithm of a given sine is a number that always increased arithmetically at the same rate at which the total sine began to decrease geometrically.

In modern notation, Napier’s kinematic model can be represented by the differential equation: dx/x = -dy/M, where M is a scale factor introduced to ensure that the value turns out to be an integer with the required number of digits (decimal fractions were not yet widely used). Napier took M = 10000000.

Strictly speaking, Napier tabulated the wrong function, which is now called the logarithm. If we denote its function LogNap(x), then it is related to the natural logarithm as follows:

Obviously, LogNap(M) = 0, that is, the logarithm of the “full sine” is zero - this is what Napier achieved with his definition. .

The main property of the Napier logarithm: if quantities form a geometric progression, then their logarithms form an arithmetic progression. However, the logarithm rules for the neper function differed from the rules for the modern logarithm.

For example, LogNap(ab) = LogNap(a) + LogNap(b) - LogNap(1).

Unfortunately, all the values in Napier's table contained a computational error after the sixth digit. However, this did not prevent the new calculation method from gaining wide popularity, and many European mathematicians, including Kepler, began compiling logarithmic tables. Just 5 years later, in 1619, London mathematics teacher John Spidell ( John Speidell) reissued Napier's tables, transformed so that they effectively became tables of natural logarithms (although Spidell retained the scaling to integers). The term "natural logarithm" was proposed by the Italian mathematician Pietro Mengoli ( Pietro Mengoli)) in the middle of the 16th century.

In the 1620s, Edmund Wingate and William Oughtred invented the first slide rule, before the advent of pocket calculators - an indispensable engineer's tool.

A close to modern understanding of logarithmization - as the inverse operation of raising to a power - first appeared with Wallis and Johann Bernoulli, and was finally legitimized by Euler in the 18th century. In the book “Introduction to the Analysis of Infinites” (1748), Euler gave modern definitions of both exponential and logarithmic functions, expanded them into power series, and especially noted the role of the natural logarithm.

Euler is also credited with extending the logarithmic function to the complex domain.

3.2. Complex logarithm

4. Logarithmic tables

Logarithmic tables

The first tables of logarithms were published by John Napier (1614), and they contained only logarithms of trigonometric functions, and with errors. Independently of him, Joost Burgi, a friend of Kepler, published his tables (1620). In 1617, Oxford mathematics professor Henry Briggs published tables that already included decimal logarithms of the numbers themselves, from 1 to 1000, with 8 (later 14) digits. But there were also errors in Briggs’ tables. The first error-free edition based on the Vega tables (1783) appeared only in 1857 in Berlin (Bremiwer tables).

In Russia, the first tables of logarithms were published in 1703 with the participation of L. F. Magnitsky. Several collections of logarithm tables were published in the USSR.

Bradis V. M. Four-digit math tables. 44th edition, M., 1973.

Bradis tables (1921) were used in educational institutions and in engineering calculations that did not require great accuracy. They contained mantissas of decimal logarithms of numbers and trigonometric functions, natural logarithms, and some other useful calculation tools.

Vega G. Tables of seven-digit logarithms, 4th edition, M., 1971.

Professional collection for precise calculations.

Five-digit tables of natural values of trigonometric quantities, their logarithms and logarithms of numbers, 6th ed., M.: Nauka, 1972.
Tables of natural logarithms, 2nd edition, in 2 volumes, M.: Nauka, 1971.

Nowadays, with the spread of calculators, the need to use tables of logarithms has disappeared.

M, Feature (complex analysis).

Definition and properties

Complex zero has no logarithm because the complex exponent does not take the value zero. Non-zero texvc can be represented in demonstrative form:

Unable to parse expression (Executable file texvc not found; See math/README - help with setup.): z=r \cdot e^(i (\varphi + 2 \pi k))\;\;, Where Unable to parse expression (Executable file texvc not found; See math/README for setup help.): k- arbitrary integer

Then Unable to parse expression (Executable file texvc not found; See math/README for setup help.): \mathrm(Ln)\,z is found by the formula:

Unable to parse expression (Executable file texvc not found; See math/README - help with setup.): \mathrm(Ln)\,z = \ln r + i \left(\varphi + 2 \pi k \right)

Here Unable to parse expression (Executable file texvc not found; See math/README for setup help.): \ln\,r= \ln\,|z|- real logarithm. It follows from this:

It is clear from the formula that one and only one of the values has an imaginary part in the interval Unable to parse expression (Executable file texvc . This value is called main importance complex natural logarithm. The corresponding (already unambiguous) function is called main branch logarithm and is denoted Unable to parse expression (Executable file texvc not found; See math/README for setup help.): \ln\,z. Sometimes through Unable to parse expression (Executable file texvc not found; See math/README for setup help.): \ln\, z also denote the value of the logarithm that does not lie on the main branch. If Unable to parse expression (Executable file texvc not found; See math/README for setup help.): z is a real number, then the principal value of its logarithm coincides with the ordinary real logarithm.

It also follows from the above formula that the real part of the logarithm is determined as follows through the components of the argument:

Unable to parse expression (Executable file texvc not found; See math/README for help with setup.): \operatorname(Re)(\ln(x+iy)) = \frac(1)(2) \ln(x^2+y^2)

The figure shows that the real part as a function of the components is centrally symmetric and depends only on the distance to the origin. It is obtained by rotating the graph of the real logarithm around the vertical axis. As it approaches zero, the function tends to Unable to parse expression (Executable file texvc not found; See math/README - help with setup.): -\infty.

The logarithm of a negative number is found by the formula:

Unable to parse expression (Executable file texvc not found; See math/README for setup help.): \mathrm(Ln) (-x) = \ln x + i \pi (2 k + 1) \qquad (x>0,\ k = 0, \pm 1 ,\pm 2\dots)

Examples of complex logarithm values

Let us present the main value of the logarithm ( Unable to parse expression (Executable file texvc not found; See math/README for setup help.): \ln) and its general expression ( Unable to parse expression (Executable file texvc not found; See math/README for setup help.): \mathrm(Ln)) for some arguments:

Unable to parse expression (Executable file texvc not found; See math/README for setup help.): \ln (1) = 0;\; \mathrm(Ln) (1) = 2k\pi i Unable to parse expression (Executable file texvc not found; See math/README for setup help.): \ln (-1) = i \pi;\; \mathrm(Ln) (-1) = (2k+1)i \pi Unable to parse expression (Executable file texvc not found; See math/README - help with setup.): \ln (i) = i \frac(\pi) (2);\; \mathrm(Ln) (i) = i \frac(4k+1)(2) \pi

Unable to parse expression (Executable file texvc not found; See math/README - help with setup.): i\pi = \ln(-1) = \ln((-i)^2) = 2\ln(-i) = 2(-i\pi/2 ) = -i\pi- an obvious mistake.

Note that on the left is the main value of the logarithm, and on the right is the value from the underlying branch ( Unable to parse expression (Executable file texvc not found; See math/README - help with setup.): k=-1). The cause of the error is careless use of the property Unable to parse expression (Executable file texvc not found; See math/README for setup help.): \log_a((b^p)) = p~\log_a b, which, generally speaking, implies in the complex case the entire infinite set of values of the logarithm, and not just the main value.

Complex logarithmic function and Riemann surface

Due to its simply connectedness, the Riemann surface of the logarithm is a universal covering for the complex plane without a point Unable to parse expression (Executable file texvc .

Analytical continuation

The logarithm of a complex number can also be defined as the analytic continuation of the real logarithm to the entire complex plane. Let the curve Unable to parse expression (Executable file texvc starts at one, does not go through zero and does not cross the negative part of the real axis. Then the principal value of the logarithm at the end point Unable to parse expression (Executable file texvc not found; See math/README for setup help.): w crooked Unable to parse expression (Executable file texvc not found; See math/README for setup help.): \Gamma can be determined by the formula:

Unable to parse expression (Executable file texvc not found; See math/README for help with setting up.): \ln z = \int\limits_\Gamma (du \over u)

If Unable to parse expression (Executable file texvc not found; See math/README for setup help.): \Gamma- a simple curve (without self-intersections), then for numbers lying on it, logarithmic identities can be used without fear, for example:

Unable to parse expression (Executable file texvc not found; See math/README for help with setup.): \ln (wz) = \ln w + \ln z, ~\forall z,w\in\Gamma\colon zw\in \Gamma

The main branch of the logarithmic function is continuous and differentiable on the entire complex plane, except for the negative part of the real axis, on which the imaginary part changes abruptly to Unable to parse expression (Executable file texvc not found; See math/README - help with setup.): 2\pi. But this fact is a consequence of the artificial limitation of the imaginary part of the main value by the interval Unable to parse expression (Executable file texvc not found; See math/README for setup help.): (-\pi, \pi]. If we consider all branches of the function, then continuity occurs at all points except zero, where the function is not defined. If you resolve the curve Unable to parse expression (Executable file texvc not found; See math/README for setup help.): \Gamma cross the negative part of the real axis, then the first such intersection transfers the result from the main value branch to the adjacent branch, and each subsequent intersection causes a similar shift along the branches of the logarithmic function (see figure).

From the analytic continuation formula it follows that on any branch of the logarithm:

Unable to parse expression (Executable file texvc not found; See math/README for setup help.): \frac(d)(dz) \ln z = (1\over z)

For any circle Unable to parse expression (Executable file texvc not found; See math/README for setup help.): S, covering the point Unable to parse expression (Executable file texvc not found; See math/README for setup help.): 0 :

Unable to parse expression (Executable file texvc not found; See math/README for help with setting up.): \oint\limits_S (dz \over z) = 2\pi i

The integral is taken in the positive direction (counterclockwise). This identity underlies the theory of residues.

One can also define the analytic continuation of the complex logarithm using series known for the real case:

However, from the form of these series it follows that at one the sum of the series is equal to zero, that is, the series relates only to the main branch of the multivalued function of the complex logarithm. The radius of convergence of both series is 1.

Connection with inverse trigonometric and hyperbolic functions

Unable to parse expression (Executable file texvc not found; See math/README for setup help.): \operatorname(Arcsin) z = -i \operatorname(Ln) (i z + \sqrt(1-z^2)) Unable to parse expression (Executable file texvc not found; See math/README for setup help.): \operatorname(Arccos) z = -i \operatorname(Ln) (z + i\sqrt(1-z^2)) Unable to parse expression (Executable file texvc not found; See math/README - help with setup.): \operatorname(Arctg) z = -\frac(i)(2) \ln \frac(1+z i)(1-z i) + k \pi \; (z \ne \pm i) Unable to parse expression (Executable file texvc not found; See math/README - help with setup.): \operatorname(Arcctg) z = -\frac(i)(2) \ln \frac(z i-1)(z i+1) + k \pi \; (z \ne \pm i) Unable to parse expression (Executable file texvc not found; See math/README for setup help.): \operatorname(Arsh)z = \operatorname(Ln)(z+\sqrt(z^2+1))- inverse hyperbolic sine Unable to parse expression (Executable file texvc not found; See math/README - help with setup.): \operatorname(Arch)z=\operatorname(Ln) \left(z+\sqrt(z^(2)-1) \right)- inverse hyperbolic cosine Unable to parse expression (Executable file texvc not found; See math/README for setup help.): \operatorname(Arth)z=\frac(1)(2)\operatorname(Ln)\left(\frac(1+z)(1-z)\right)- inverse hyperbolic tangent Unable to parse expression (Executable file texvc not found; See math/README for setup help.): \operatorname(Arcth)z=\frac(1)(2)\operatorname(Ln)\left(\frac(z+1)(z-1)\right)- inverse hyperbolic cotangent

Historical sketch

The first attempts to extend logarithms to complex numbers were made at the turn of the 17th-18th centuries by Leibniz and Johann Bernoulli, but they failed to create a holistic theory, primarily because the very concept of logarithm was not yet clearly defined. The discussion on this issue took place first between Leibniz and Bernoulli, and in the middle of the 18th century between D’Alembert and Euler. Bernoulli and D'Alembert believed that it should be determined Unable to parse expression (Executable file texvc not found; See math/README for setup help.): \log(-x) = \log(x), while Leibniz proved that the logarithm of a negative number is an imaginary number. The complete theory of logarithms of negative and complex numbers was published by Euler in 1747-1751 and is essentially no different from the modern one. Although the debate continued (D'Alembert defended his point of view and argued it in detail in an article in his Encyclopedia and in other works), Euler's approach received universal recognition by the end of the 18th century.

Write a review about the article "Complex logarithm"

Literature

Theory of logarithms

Korn G., Korn T.. - M.: Nauka, 1973. - 720 p.
Sveshnikov A. G., Tikhonov A. N. Theory of functions of a complex variable. - M.: Nauka, 1967. - 304 p.
Fikhtengolts G. M. Course of differential and integral calculus. - ed. 6th. - M.: Nauka, 1966. - 680 p.

History of logarithms

Mathematics of the 18th century // / Edited by A. P. Yushkevich, in three volumes. - M.: Science, 1972. - T. III.
Kolmogorov A. N., Yushkevich A. P. (eds.). Mathematics of the 19th century. Geometry. Theory of analytic functions. - M.: Science, 1981. - T. II.

Notes

Logarithmic function. // . - M.: Soviet Encyclopedia, 1982. - T. 3.
, Volume II, pp. 520-522..
, With. 623..
, With. 92-94..
, With. 45-46, 99-100..
Boltyansky V. G., Efremovich V. A.. - M.: Nauka, 1982. - P. 112. - (Kvant Library, issue 21).
, Volume II, pp. 522-526..
, With. 624..
, With. 325-328..
Rybnikov K. A. History of mathematics. In two volumes. - M.: Publishing house. Moscow State University, 1963. - T. II. - P. 27, 230-231..
, With. 122-123..
Klein F.. - M.: Science, 1987. - T. II. Geometry. - pp. 159-161. - 416 s.

An excerpt characterizing the Complex logarithm

From the wild horror that gripped us, we rushed like bullets across a wide valley, not even thinking that we could quickly go to another “floor”... We simply did not have time to think about it - we were too scared.
The creature flew right above us, loudly clicking its gaping toothy beak, and we rushed as fast as we could, splashing vile slimy splashes to the sides, and mentally praying that something else would suddenly interest this creepy “miracle bird”... It was felt. that she was much faster and we simply had no chance to break away from her. As luck would have it, not a single tree grew nearby, there were no bushes, or even stones behind which one could hide, only an ominous black rock could be seen in the distance.
- There! – Stella shouted, pointing her finger at the same rock.
But suddenly, unexpectedly, right in front of us, a creature appeared from somewhere, the sight of which literally froze our blood in our veins... It appeared as if “straight out of thin air” and was truly terrifying... The huge black carcass was completely covered long, coarse hair, making him look like a pot-bellied bear, only this “bear” was as tall as a three-story house... The monster’s lumpy head was “crowned” with two huge curved horns, and the eerie mouth was decorated with a pair of incredibly long fangs, sharp as knives, just by looking to which, with fright, our legs gave way... And then, incredibly surprising us, the monster easily jumped up and... picked up the flying “muck” on one of its huge fangs... We froze in shock.
- Let's run!!! – Stella squealed. – Let’s run while he’s “busy”!..
And we were ready to rush again without looking back, when suddenly a thin voice sounded behind our backs:
- Girls, wait!!! No need to run away!.. Dean saved you, he is not an enemy!
We turned around sharply - a tiny, very beautiful black-eyed girl was standing behind us... and was calmly stroking the monster that had approached her!.. Our eyes widened in surprise... It was incredible! Certainly - it was a day of surprises!.. The girl, looking at us, smiled welcomingly, not at all afraid of the furry monster standing next to us.
- Please don't be afraid of him. He is very kind. We saw that Ovara was chasing you and decided to help. Dean was great, he made it on time. Really, my dear?
“Good” purred, which sounded like a slight earthquake, and, bending his head, licked the girl’s face.
– Who is Owara, and why did she attack us? – I asked.
“She attacks everyone, she’s a predator.” And very dangerous,” the girl answered calmly. – May I ask what you are doing here? You're not from here, girls?
- No, not from here. We were just walking. But the same question for you - what are you doing here?
“I’m going to see my mother...” the little girl became sad. “We died together, but for some reason she ended up here.” And now I live here, but I don’t tell her this, because she will never agree with it. She thinks I'm just coming...
– Isn’t it better to just come? It’s so terrible here!.. – Stella shrugged her shoulders.
“I can’t leave her here alone, I’m watching her so that nothing happens to her.” And here Dean is with me... He helps me.
I just couldn’t believe it... This little brave girl voluntarily left her beautiful and kind “floor” to live in this cold, terrible and alien world, protecting her mother, who was very “guilty” in some way! I don’t think there would be many people so brave and selfless (even adults!) who would dare to undertake such a feat... And I immediately thought - maybe she just didn’t understand what she was going to doom herself to?!
– How long have you been here, girl, if it’s not a secret?
“Recently...” the black-eyed baby answered sadly, tugging at a black lock of her curly hair with her fingers. – I found myself in such a beautiful world when I died!.. He was so kind and bright!.. And then I saw that my mother was not with me and rushed to look for her. It was so scary at first! For some reason she was nowhere to be found... And then I fell into this terrible world... And then I found her. I was so scared here... So lonely... Mom told me to leave, she even scolded me. But I can’t leave her... Now I have a friend, my good Dean, and I can already somehow exist here.
Her “good friend” growled again, which gave Stella and me huge “lower astral” goosebumps... Having collected myself, I tried to calm down a little and began to take a closer look at this furry miracle... And he, immediately feeling that he was noticed, he terribly bared his fanged mouth... I jumped back.
- Oh, don't be afraid, please! “He’s smiling at you,” the girl “reassured.”
Yeah... You'll learn to run fast from such a smile... - I thought to myself.
- How did it happen that you became friends with him? – Stella asked.
– When I first came here, I was very scared, especially when such monsters as you were attacking today. And then one day, when I almost died, Dean saved me from a whole bunch of creepy flying “birds”. I was also scared of him at first, but then I realized what a heart of gold he has... He is the best friend! I never had anything like this, even when I lived on Earth.
- How did you get used to it so quickly? His appearance is not quite, let’s say, familiar...
– And here I understood one very simple truth, which for some reason I did not notice on Earth - appearance does not matter if a person or creature has a good heart... My mother was very beautiful, but at times she was very angry too. And then all her beauty disappeared somewhere... And Dean, although scary, is always very kind, and always protects me, I feel his kindness and am not afraid of anything. But you can get used to the appearance...
– Do you know that you will be here for a very long time, much longer than people live on Earth? Do you really want to stay here?..
“My mother is here, so I have to help her.” And when she “leaves” to live on Earth again, I will also leave... To where there is more goodness. In this terrible world, people are very strange - as if they don’t live at all. Why is that? Do you know anything about this?
– Who told you that your mother would leave to live again? – Stella became interested.
- Dean, of course. He knows a lot, he’s lived here for a very long time. He also said that when we (my mother and I) live again, our families will be different. And then I won’t have this mother anymore... That’s why I want to be with her now.
- How do you talk to him, your Dean? – Stella asked. - And why don’t you want to tell us your name?
But it’s true – we still didn’t know her name! And they didn’t know where she came from either...
– My name was Maria... But does that really matter here?
- Surely! – Stella laughed. - How can I communicate with you? When you leave, they will give you a new name, but while you are here, you will have to live with the old one. Did you talk to anyone else here, girl Maria? – Stella asked, jumping from topic to topic out of habit.
“Yes, I talked...” the little girl said hesitantly. “But they are so strange here.” And so unhappy... Why are they so unhappy?
– Is what you see here conducive to happiness? – I was surprised by her question. – Even the local “reality” itself kills any hopes in advance!.. How can you be happy here?
- Don't know. When I’m with my mother, it seems to me that I could be happy here too... True, it’s very scary here, and she really doesn’t like it here... When I said that I agreed to stay with her, she yelled at me and said that I’m her “brainless misfortune”... But I’m not offended... I know that she’s just scared. Just like me...
– Perhaps she just wanted to protect you from your “extreme” decision, and only wanted you to go back to your “floor”? – Stella asked carefully, so as not to offend.
– No, of course... But thank you for the good words. Mom often called me not very good names, even on Earth... But I know that this was not out of anger. She was simply unhappy that I was born, and often told me that I ruined her life. But it wasn't my fault, was it? I always tried to make her happy, but for some reason I wasn’t very successful... And I never had a dad. – Maria was very sad, and her voice was trembling, as if she was about to cry.
Stella and I looked at each other, and I was almost sure that similar thoughts visited her... I already really didn’t like this spoiled, selfish “mother”, who, instead of worrying about her child herself, did not care about his heroic sacrifice at all I understood and, in addition, I also hurt her painfully.
“But Dean says that I’m good, and that I make him very happy!” – the little girl babbled more cheerfully. “And he wants to be friends with me.” And others I've met here are very cold and indifferent, and sometimes even evil... Especially those who have monsters attached...
“Monsters—what?..” we didn’t understand.
- Well, they have terrible monsters sitting on their backs and telling them what they must do. And if they don’t listen, the monsters mock them terribly... I tried to talk to them, but these monsters won’t allow me.
We understood absolutely nothing from this “explanation,” but the very fact that some astral beings were torturing people could not remain “explored” by us, so we immediately asked her how we could see this amazing phenomenon.
- Oh, yes everywhere! Especially at the “black mountain”. There he is, behind the trees. Do you want us to go with you too?
- Of course, we will be only too happy! – the delighted Stella immediately answered.
To be honest, I also didn’t really smile at the prospect of dating someone else, “creepy and incomprehensible,” especially alone. But interest overcame fear, and we, of course, would have gone, despite the fact that we were a little afraid... But when such a defender as Dean walked with us, it immediately became more fun...
And then, after a short moment, real Hell unfolded before our eyes, wide open with amazement... The vision was reminiscent of the paintings of Bosch (or Bosc, depending on what language you translate it into), a “crazy” artist who once shocked the whole world with his art world... He, of course, was not crazy, but was simply a seer who for some reason could only see the lower Astral. But we must give him credit - he portrayed him superbly... I saw his paintings in a book that was in my dad’s library, and I still remembered the eerie feeling that most of his paintings carried...
“What a horror!..” whispered the shocked Stella.
One could probably say that we have already seen a lot here, on the “floors”... But even we were not able to imagine this in our most terrible nightmare!.. Behind the “black rock” something completely opened up unthinkable... It looked like a huge, flat “cauldron” carved into the rock, at the bottom of which crimson “lava” was bubbling... The hot air “burst” everywhere with strange flashing reddish bubbles, from which scalding steam burst out and fell in large drops to the ground, or to the people who fell under it at that moment... Heartbreaking screams were heard, but immediately fell silent, as the most disgusting creatures sat on the backs of the same people, who with a contented look “controlled” their victims, not paying the slightest attention to their suffering... Under the naked feet of people, hot stones turned red, the crimson earth, bursting with heat, bubbled and “melted”... Splashes of hot steam burst through huge cracks and, burning the feet of human beings sobbing in pain, were carried into the heights, evaporating with a light smoke ... And in the very middle of the “pit” flowed a bright red, wide fiery river, into which, from time to time, the same disgusting monsters unexpectedly threw one or another tormented entity, which, falling, caused only a short splash of orange sparks, and then but, turning for a moment into a fluffy white cloud, it disappeared... forever... It was real Hell, and Stella and I wanted to “disappear” from there as soon as possible...
“What are we going to do?” Stella whispered in quiet horror. - Do you want to go down there? Is there anything we can do to help them? Look how many there are!..
We stood on a black-brown, heat-dried cliff, observing the horror-filled “mash” of pain, hopelessness, and violence stretching below, and we felt so childishly powerless that even my warlike Stella this time categorically folded her ruffled “wings.” “and was ready at the first call to rush off to her own, so dear and reliable, upper “floor”...

Real logarithm

Properties

Natural logarithms

Decimal logarithms

Complex logarithm

Multivalued function

Riemann surface

Historical sketch

Real logarithm

Complex logarithm

Logarithmic tables

2. Euler's formulas.

3. Natural logarithm of a complex number.

2. Euler's formulas.

3. Natural logarithm of a complex number.

Plan:

Introduction

1. Real logarithm

1.1. Properties

1.2. Logarithmic function

1.3. Natural logarithms

1.4. Decimal logarithms

2. Complex logarithm

2.1. Definition and properties

2.2. Examples

2.3. Analytical continuation

2.4. Riemann surface

3. Historical sketch

3.1. Real logarithm

3.2. Complex logarithm

4. Logarithmic tables

Definition and properties

Examples of complex logarithm values

Complex logarithmic function and Riemann surface

Analytical continuation

Connection with inverse trigonometric and hyperbolic functions

Historical sketch

Write a review about the article "Complex logarithm"

Literature

Notes

An excerpt characterizing the Complex logarithm

Read also