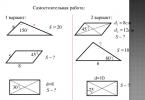
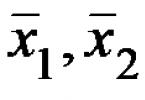Independent work:

Option 2:

Option 1:

Check the answers:

Option 2:

Option 1:

Cosine theorem:

The square of a side of a triangle is equal to the sum of the squares of the other two sides minus twice the product of these sides and the cosine of the angle between them

• The most ancient proof for the theorem of sines on a plane is described in the book by Nasir ad-Din At-Tusi, “Treatise on the Complete Quadrilateral,” written in the 13th century. The sine theorem for a spherical triangle was proven by mathematicians of the medieval East back in the 10th century. In the 11th century work of Al-Jayani, “The Book of the Unknown Arcs of the Sphere,” a general proof of the theorem of sines on the sphere was given

Nasir ad-Din At-Tusi

Theorem of sines :

The sides of a triangle are proportional to the sines of the opposite angles

• Comment: It can be proven that the ratio of the side of a triangle to the sine of the opposite angle is equal to the diameter of the circumscribed circle. Therefore, for any triangle ABC with sides AB=c, BC=a, CA=b the following equalities hold:
• Where R is the radius of the circumscribed circle.

1) Write down the sine theorem for this triangle:

2) Write down the cosine theorem to calculate the side of the MC:

Find angle B.

Find the length of side BC.

Find the length of side AB.

Find MN.

Write down the formula for calculation:

• http://ppt4web.ru/geometrija/teoremy-sinusov-i-kosinusov0.html
• http://nsportal.ru/shkola/geometriya/library/2014/10/15/teorema-sinusov-i-kosinusov
• https://upload.wikimedia.org/wikipedia/commons/thumb/1/14/Johannes_Regiomontanus2.jpg/500px-Johannes_Regiomontanus2.jpg
• http://img1.liveinternet.ru/images/attach/c/10/110/217/110217775_Nesreddi_tusi.jpg
• http://www.biografguru.ru/about/evklid/?q=3117

Theorems of sines and cosines in problems with practical content

are true?

Exercise 1

the products of these parties to sin angle between them.

The square of any side of the trolley is equal to the sum

squares of the other two sides without

the products of these parties to cos angle between them.

The square of any side of the trolley is equal to the sum

squares of the other two sides without double

the products of these parties to cos angle between them.

In a right triangle

the square of a leg is equal to the difference of squares

hypotenuse and other leg.

Which of the following statements are true?

Task 2

sines of opposite angles.

The sides of the triangle are proportional

cosines of opposite angles.

The sides of the triangle are proportional

sines of adjacent angles.

The sides of the triangle are proportional

opposite angles.

Which of the following statements are true?

Task 3

area and perimeter.

Solving a triangle means measuring everything

its elements.

Solving a triangle means finding it

unknown elements from three known ones.

Solving a triangle means finding it

equal triangle.

Wrong!

Wrong!

Wrong!

Match?

Task 4

A) theorem of sines

B) Heron's formula

B) Pythagorean theorem

D) cosine theorem

A 1.7 m tall man stands at a distance

8 steps from the pole on which the lantern hangs.

A person's shadow is equal to four steps. On what

height (in meters) is the lantern located?

Task 5

8 steps

4 steps

Hint (2)

Consider similar triangles

Δ ABC

Δ AKM

The Hedgehog has the soccer ball, which is located at distances of 23 m and 24 m from the goal posts. The width of the goal is 7 m. Find the angle at which the ball hits the goal?

Task 6

Task 7

Algorithm for solving practical problems

• Execute drawing
• Solve a geometric problem

Task 7

Find the distance to an inaccessible object

Algorithm for finding the distance to an inaccessible object

• Mark 2 points, the distance between which can be measured
• Take angle measurements
• Build a mathematical model (drawing)
• Solve a geometric problem using the sine theorem

Using the data given in the figure, find the width AB of the lake. Please indicate the whole number of meters in your answer.

Decide for yourself 1 option To determine the width of the river (AC), 2 points C and B were marked at a distance of 50m from each other. We measured the angles ACB and ABC, where A is a tree standing on the other side of the river at the water's edge. (<АCВ=550, <АВС=650) Option 2 To determine the width of the river (AC), 2 points B and C were marked at a distance of 40m from each other. We measured the angles ACB and ABC, where A is a tree standing on the other side of the river at the water's edge. (<АCВ=600, <АВС=700) Проверьте друг друга <А=1800-600-700= 50 0 AВ = 49 м

Subject « Cosine theorem"

Lesson type : a lesson in learning new knowledge

Lesson location – the first lesson on this topic

Learning Objective of the Lesson :

students’ knowledge of the formulation of the cosine theorem;

skill:

find the length of the third side from the known two others and the angle

between them;

determine the angle (cosine of the angle) of a triangle using three known

to the parties;

determine the type of triangle based on three known sides.

Personal development tasks:

organize situations for:

self-determination of students on the predicted result

cognitive activity;

development of reflexive abilities;

create conditions for:

development of students' communication abilities;

development of students’ thinking, ability to argue and prove.

Equipment and materials: multimedia installation, screen, board, chalk.

Brief Lesson Plan

1. Organizing time.

2. Updating leading knowledge and methods of action.

3. Motivation and goal setting.

4. Main part. Proof of the cosine theorem. Performance

examples of the application of the cosine theorem in solving problems.

Independent application of knowledge. (Mini test).

5. Reflection. Summing up the lesson.

During the classes

Stage 1 Organizational. I greet students and check the readiness of the schoolchildren’s workplace for the training session. I create the mood for work, I announce to students that during the lesson they evaluate themselves by putting marks on the work card.

Stage 2Updating students' knowledge, putting forward a hypothesis.

To begin with, I suggest a warm-up (test) using the formulas “Reduction formulas”, “Values ​​of sine, cosine and tangent for angles from 0⁰ to 180⁰”.

Write down the formula for finding the distance between points using their coordinates.

Stage 3 Creating a problem situation and resolving it.Motivation and goal setting.

A problematic task increases students’ motivation for further cognitive activity. A situation is organized to set the goal of the lesson and predict the results of the lesson, for example, it is necessary to find out a universal way to find the length of the third side of a triangle based on the known lengths of the other two sides and the angle between them.

Group work.

The solution of the problem . Task. Using the formula for the distance between points, find the length of side BC▲ ABC, if A(0;0), B(c;0), C(bcosA ; bsinA ).

Conclusion: Let us give a verbal formulation of the resulting equality. We obtain a theorem called cosine theorem:

The square of a side of a triangle is equal to the sum of the squares of the other two sides minus twice the product of these sides and the cosine of the angle between them.

One of the most beautiful and simple proofs of the cosine theorem is its proof in the coordinate plane.

Can we say that the Pythagorean theorem is a special case of the cosine theorem? Yes, because cos 90 o =0.

Stage 4 Fizminutka.

Stage 6 Statement of the problem: how many elements must be known for the problem to be solved? Build a model, determine the type of problem, explore the relationships and connections between the elements of the triangle .

Question for discussion Denia. What problem can be solved using the cosine theorem?

Knowing that has the form a 2 =b 2 +c 2 - 2bc×cosγ, transform this expression so that the desired value becomes the angle γ: b 2 +c 2 =2bc×cosγ+a 2 .
Then provide what is shown equation to a slightly different form: b 2 +c 2- a 2 =2bc×cosγ. This expression then follows in the one below:

cosγ=√b 2 +c 2 -a2/2bc.
Question for discussion Denia. What can you find using this formula?

The value of the cosine of an angle in a triangle.

Students are asked to calculate the cosine of the largest angle in a triangle with known lengths of three sides and determine the type of this triangle.

Calculate the cosine of the larger angle in a triangle if its sides are equal:

Option No. 1

Option No. 2

Option #3

c = 6, b = 8, a = 9

c = 6, b = 8, a = 10

c = 6, b = 8, a = 11

cos 19/96

cos 0

cos 0

79 0

90 0

103 0

The calculation results of each group are entered into a table, discussed, and conclusions are drawn:

To determine the type of triangle (acute, rectangular, obtuse)

necessary:

Calculate the cosine of the angle opposite the larger side;

If cos 0, acute triangle;

If cos 0, right triangle;

If cos 0, the triangle is obtuse.

Question for discussion Denia.How can you answer this question without calculating the cosine of the largest angle? I recall the theorem about the relationship between the sides and angles of a triangle. (In a triangle, the larger angle lies opposite the larger side and, conversely, the larger side lies opposite the larger angle).

CONCLUSION.

Let c be the largest side
- If With 2 < a 2 + b 2, then the triangle is acute;
- If With 2 = a 2 + b 2, then the triangle is right-angled;
- If With 2 >a 2 + b 2, then the triangle is obtuse.

Check the output on completed tasks (at home).

Stage 7. Building a long-term plan for further work.

- teacher question : Question for discussion. What problems can be solved using the cosine theorem?

-students' answers

find the length of the third side from the known two others and the angle between them;

determine the angle (cosine of the angle) of a triangle based on three known sides

determine the type of triangle based on three known sides

Stage 5 Consolidation. Mini-tes

Mini test

Condition

Answer options

In a triangle with sides m , n , p against the party

p lies the angle α . Then the following is true

formula:

A) m 2 n 2 p 2 2 n.p. cosα

B) m n 2 p 2 2 n.p. cos α

IN) p 2 m 2 n 2 mn cos α ;

G) p m 2 n 2 mn cos α ;

If the cosine of the larger angle of a triangle

is negative, then this triangle:

A) acute-angled; B) rectangular;

IN) obtuse.

The lengths of two sides of a triangle are equal and 3, and the angle

there are 45 0 between them. Then the length of the third side is:

A) 2; B) 3; B) √ 5; G) 5

In a triangle, the lengths of the sides are √3; 4; √7. Determine the type of triangle

A) acute-angled; B) rectangular;

IN) obtuse.

Examination.

Answer options

1

IN) p 2 m 2 n 2 mn cosα ;

2

IN) obtuse.

3

B)√ 5

4

IN) obtuse

What else needs to be done to complete the lesson?

Students: “Assign homework.”

Teacher: “If you were a teacher, what homework would you assign?”

Stage 8 Homework. P.98, No. 1025(d).

I propose to put a final mark on the work cards and conduct reflection on filling out the table.

Discussion of filling out the table. Ratings

Applications No. 1. Warm-up. Test

“Reduction formulas”, “Values ​​of sine, cosine and tangent for angles from 0⁰ to 180⁰”

1. sin (90 ⁰ - α ) =

2. cos (90 ⁰ - α ) =

3. sin (180 ⁰ - α ) = 1. cosα 2. sinα 3. - cosα 4. - sinα

4. cos (180 ⁰ - α ) 1) cosα 2) sinα 3) - cosα 4) - sinα

5. cos 60 ⁰ = 1) 2) 3)

6. cos 30 ⁰ = 1) 2) 3)

To use presentation previews, create a Google account and log in to it: https://accounts.google.com

Slide captions:

Theorem of sines

Theorem 12.2 (theorem of sines) The sides of a triangle are proportional to the sines of the opposite angles.

C В A a sinA b sinB = = c sinC a b c The sides of the triangle are proportional to the sines of the opposite angles.

M O X MO sinX MX sinO = = OX sinC The sides of a triangle are proportional to the sines of the opposite angles.

C D E CD sinE EC sinD = = DE sinC The sides of a triangle are proportional to the sines of the opposite angles.

Corollary from the theorem of sines where R is the radius of a circle circumscribed about ∆ ABC

Problem Find the radius of a circle circumscribed about ∆ ABC, if AC = 2 cm, ABC = 45° A C B 45 0 2 By consequence of the theorem of sines R = R = 2: (2 ·) R =

Trigonometric table No. 1 No. 2 No. 3 No. 4 No. 5

AB sinC AC sinB = C A B 75 0 60 0 60 0 4 4 ? 45 0 45 0 Find AB Problem No. 1 Table

AB sinC BC sinA = C A B 60 0 60 0 ? 2 3 3 2 Problem No. 2 Table

2 AB sinC AC sinB = C A B ? 2 2 2 2 2 13 5 0 13 5 0 Find angle A Problem No. 3 Table

120 0 AC sinD AD sinC = AB C D is a parallelogram. Find AC. D A B C 30 0 30 0 6 0 0 5 5 ? 120 0 30 0 Problem No. 4 Table

45 0 2 45 0 BC sinA AB sinC = AB C D is a parallelogram. Find BC. D A B C 30 0 30 0 2 ? 105 0 30 0 Problem No. 5 Table

Homework Page 162-163, paragraph 110; prove Theorem 12.2; according to workbook No. 99 – 104

On the topic: methodological developments, presentations and notes

An interactive test that contains 5 tasks with the choice of one correct answer out of four proposed, taking into account the time spent on passing the test; The test was created in PowerPoint-2007 with...

Lesson - Solving problems in geometry 9th grade. "Area of ​​a triangle. Theorem of sines. Theorem of cosines."

Problem solving involves the ability to apply knowledge under standard conditions or with slight deviations from them. Also considered are tasks that require the ability to apply knowledge in complex...