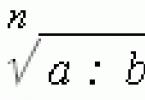
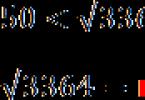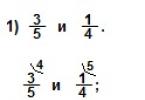Gana dažnai spręsdami problemas susiduriame su dideliais skaičiais, iš kurių reikia išgauti Kvadratinė šaknis. Daugelis mokinių nusprendžia, kad tai klaida, ir pradeda spręsti visą pavyzdį. Jokiu būdu tai neturėtų būti daroma! Tam yra dvi priežastys:

1. Didelio skaičiaus šaknys atsiranda problemose. Ypač tekste;
2. Yra algoritmas, pagal kurį šios šaknys laikomos beveik žodžiu.

Šiandien mes apsvarstysime šį algoritmą. Galbūt kai kurie dalykai jums atrodys nesuprantami. Bet jei atkreipsite dėmesį į šią pamoką, gausite galingiausią ginklą prieš kvadratinės šaknys.

Taigi algoritmas:

1. Apribokite norimą šaknį aukščiau ir žemiau iki 10 kartotinių. Taigi paieškos diapazoną sumažinsime iki 10 skaičių;
2. Iš šių 10 skaičių išrinkite tuos, kurie tikrai negali būti šaknys. Dėl to išliks 1-2 skaičiai;
3. Padėkite šiuos 1–2 skaičius kvadratu. Ta iš jų, kurios kvadratas lygus pradiniam skaičiui, bus šaknis.

Prieš taikydami šį algoritmą praktiškai, pažvelkime į kiekvieną atskirą žingsnį.

Šaknų apribojimas

Visų pirma, turime išsiaiškinti, tarp kurių skaičių yra mūsų šaknis. Labai pageidautina, kad skaičiai būtų dešimties kartotiniai:

10 2 = 100;
20 2 = 400;
30 2 = 900;
40 2 = 1600;
...
90 2 = 8100;
100 2 = 10 000.

Gauname skaičių seką:

100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.

Ką mums duoda šie skaičiai? Tai paprasta: mes nustatome ribas. Paimkime, pavyzdžiui, skaičių 1296. Jis yra tarp 900 ir 1600. Todėl jo šaknis negali būti mažesnė nei 30 ir didesnė nei 40:

[Paveikslo antraštė]

Tas pats pasakytina apie bet kurį kitą skaičių, iš kurio galite rasti kvadratinę šaknį. Pavyzdžiui, 3364:

[Paveikslo antraštė]

Taigi vietoj nesuprantamo skaičiaus gauname labai konkretų diapazoną, kuriame yra pradinė šaknis. Norėdami dar labiau susiaurinti paieškos apimtį, pereikite prie antro veiksmo.

Akivaizdžiai nereikalingų skaičių pašalinimas

Taigi, turime 10 skaičių – kandidatų į šaknį. Juos gavome labai greitai, be kompleksinio mąstymo ir dauginimo stulpelyje. Laikas judėti į priekį.

Tikėkite ar ne, dabar kandidatų skaičių sumažinsime iki dviejų – ir vėl be jokių sudėtingų skaičiavimų! Pakanka žinoti specialią taisyklę. Štai jis:

Paskutinis kvadrato skaitmuo priklauso tik nuo paskutinio skaitmens originalus numeris.

Kitaip tariant, užtenka pažvelgti į paskutinį kvadrato skaitmenį – ir iš karto suprasime, kur baigiasi pradinis skaičius.

Yra tik 10 skaitmenų, kurie gali būti paskutinėje vietoje. Pabandykime išsiaiškinti, kuo jie virsta kvadratu. Pažvelkite į lentelę:

1	2	3	4	5	6	7	8	9	0
1	4	9	6	5	6	9	4	1	0

Ši lentelė yra dar vienas žingsnis apskaičiuojant šaknį. Kaip matote, antroje eilutėje esantys skaičiai buvo simetriški penkių atžvilgiu. Pavyzdžiui:

2 2 = 4;
8 2 = 64 → 4.

Kaip matote, paskutinis skaitmuo abiem atvejais yra vienodas. O tai reiškia, kad, pavyzdžiui, 3364 šaknis būtinai baigiasi 2 arba 8. Kita vertus, prisimename ankstesnės pastraipos apribojimą. Mes gauname:

[Paveikslo antraštė]

Raudoni kvadratai rodo, kad mes dar nežinome šio skaičiaus. Bet juk šaknis yra tarp 50 ir 60, ant kurių yra tik du skaičiai, kurie baigiasi 2 ir 8:

[Paveikslo antraštė]

Tai viskas! Iš visų galimų šaknų palikome tik dvi galimybes! Ir tai sunkiausiu atveju, nes paskutinis skaitmuo gali būti 5 arba 0. Ir tada liks vienintelis kandidatas į šaknis!

Galutiniai skaičiavimai

Taigi, mums liko 2 kandidatų numeriai. Kaip žinoti, kuris iš jų yra šaknis? Atsakymas akivaizdus: abu skaičius kvadratu. Kvadratas duos pradinį skaičių ir bus šaknis.

Pavyzdžiui, skaičiui 3364 radome du kandidatų skaičius: 52 ir 58. Padėkime juos kvadratu:

52 2 \u003d (50 +2) 2 \u003d 2500 + 2 50 2 + 4 = 2704;
58 2 \u003d (60 - 2) 2 \u003d 3600 - 2 60 2 + 4 \u003d 3364.

Tai viskas! Paaiškėjo, kad šaknis yra 58! Tuo pačiu, siekdamas supaprastinti skaičiavimus, panaudojau sumos ir skirtumo kvadratų formulę. Dėl to jums net nereikėjo dauginti skaičių stulpelyje! Tai dar vienas skaičiavimų optimizavimo lygis, bet, žinoma, visiškai neprivalomas :)

Šakninio skaičiavimo pavyzdžiai

Teorija, žinoma, gera. Bet išbandykime tai praktiškai.

[Paveikslo antraštė]

Pirmiausia išsiaiškinkime, tarp kurių skaičių yra skaičius 576:

400 < 576 < 900
20 2 < 576 < 30 2

Dabar pažiūrėkime į paskutinį skaičių. Jis lygus 6. Kada tai atsitinka? Tik jei šaknis baigiasi 4 arba 6. Gauname du skaičius:

Belieka kiekvieną skaičių pakelti kvadratu ir palyginti su originalu:

24 2 = (20 + 4) 2 = 576

Puiku! Pirmasis kvadratas pasirodė lygus pradiniam skaičiui. Taigi tai yra šaknis.

Užduotis. Apskaičiuokite kvadratinę šaknį:

[Paveikslo antraštė]

900 < 1369 < 1600;
30 2 < 1369 < 40 2;

Pažiūrėkime į paskutinį skaičių:

1369 → 9;
33; 37.

Padėkime kvadratu:

33 2 = (30 + 3) 2 = 900 + 2 30 3 + 9 \u003d 1089 ≠ 1369;
37 2 \u003d (40 - 3) 2 \u003d 1600 - 2 40 3 + 9 = 1369.

Štai atsakymas: 37.

Užduotis. Apskaičiuokite kvadratinę šaknį:

[Paveikslo antraštė]

Apribojame skaičių:

2500 < 2704 < 3600;
50 2 < 2704 < 60 2;

Pažiūrėkime į paskutinį skaičių:

2704 → 4;
52; 58.

Padėkime kvadratu:

52 2 = (50 + 2) 2 = 2500 + 2 50 2 + 4 = 2704;

Gavome atsakymą: 52. Antrojo skaičiaus kvadratuoti nebereikės.

Užduotis. Apskaičiuokite kvadratinę šaknį:

[Paveikslo antraštė]

Apribojame skaičių:

3600 < 4225 < 4900;
60 2 < 4225 < 70 2;

Pažiūrėkime į paskutinį skaičių:

4225 → 5;
65.

Kaip matote, po antro žingsnio lieka tik viena parinktis: 65. Tai norima šaknis. Bet vis tiek išlyginkime ir patikrinkime:

65 2 = (60 + 5) 2 = 3600 + 2 60 5 + 25 = 4225;

Viskas teisinga. Užrašome atsakymą.

Išvada

Deja, ne geriau. Pažvelkime į priežastis. Yra du iš jų:

• Draudžiama naudoti skaičiuokles per bet kokį įprastą matematikos egzaminą, nesvarbu, ar tai būtų GIA, ar vieningas valstybinis egzaminas. O jei į klasę nešiojasi skaičiuotuvą, jie gali būti lengvai išmesti iš egzamino.
• Nebūk kaip kvaili amerikiečiai. Kurie nėra kaip šaknys – negali pridėti dviejų pirminių skaičių. Ir matydami trupmenas jie paprastai apima isteriją.

Operacijos su galiomis ir šaknimis. Laipsnis su neigiamu ,

nulis ir trupmena indikatorius. Apie posakius, kurie neturi prasmės.

Operacijos su laipsniais.

1. Dauginant laipsnius su ta pačia baze, pridedami jų rodikliai:

esu · a n = a m + n .

2. Dalijant laipsnius su tuo pačiu pagrindu, jų rodikliai atimta .

3. Dviejų ar daugiau veiksnių sandaugos laipsnis yra lygus šių veiksnių laipsnių sandaugai.

(abc… ) n = a n· b n · c n…

4. Santykio laipsnis (trupmena) lygus dividendo (skaitiklio) ir daliklio (vardiklio) laipsnių santykiui:

(a/b ) n = a n / b n .

5. Didinant laipsnį iki laipsnio, jų rodikliai dauginami:

(esu ) n = a m n .

Visos aukščiau pateiktos formulės skaitomos ir vykdomos abiem kryptimis iš kairės į dešinę ir atvirkščiai.

PAVYZDYS (2 · 3 · 5/15)² = 2² 3² 5² / 15² = 900 / 225 = 4 .

Operacijos su šaknimis. Visose toliau pateiktose formulėse simbolis reiškia aritmetinė šaknis(radikali išraiška yra teigiama).

1. Kelių veiksnių sandaugos šaknis yra lygi sandaugai šių veiksnių šaknys:

2. Santykio šaknis yra lygi dividendo ir daliklio šaknų santykiui:

3. Keliant šaknį į galią, pakanka pakelti iki šios galios šakninis numeris:

4. Jei padidinsime šaknies laipsnį m vieną kartą ir vienu metu pakelti į m laipsnis yra šakninis skaičius, tada šaknies reikšmė nepasikeis:

5. Jei sumažinsime šaknies laipsnį m ištraukite šaknį vieną kartą ir tuo pačiu metu m laipsnis nuo radikalaus skaičiaus, tada šaknies reikšmė nėra pasikeis:

Laipsnio sąvokos išplėtimas. Iki šiol laipsnius vertinome tik su natūraliu rodikliu; bet veiksmai laipsniai ir šaknys taip pat gali sukelti neigiamas, nulis ir trupmeninis rodikliai. Visiems šiems rodikliams reikia papildomo apibrėžimo.

Laipsnis su neigiamu rodikliu. Kai kurių skaičių galia su neigiamas (visas) rodiklis apibrėžiamas kaip vienetas, padalintas iš iki to paties skaičiaus laipsnio, kurio rodiklis lygus absoliučiajai reikšmeineigiamas rodiklis:

T dabar formulė esu: a n= esu - n gali būti naudojamas ne tikm, daugiau nei n, bet ir adresu m, mažiau nei n .

PAVYZDYS a 4 :a 7 = a 4 - 7 = a - 3 .

Jei norime formulėsesu : a n= esu - nbuvo sąžiningasm = n, mums reikia nulinio laipsnio apibrėžimo.

Laipsnis su nuliniu rodikliu. Bet kurio nulinio skaičiaus, kurio rodiklis nulinis, laipsnis yra 1.

PAVYZDŽIAI. 2 0 = 1, ( – 5) 0 = 1, (– 3 / 5) 0 = 1.

Laipsnis su trupmeniniu rodikliu. Norėdami padidinti tikrąjį skaičių ir galiai m / n , reikia išgauti šaknį n-oji galia iš m šio skaičiaus laipsnį a :

Apie posakius, kurie neturi prasmės. Yra keletas tokių posakių. bet koks skaičius.

Iš tiesų, jei manysime, kad ši išraiška yra lygi tam tikram skaičiui x, tada pagal padalijimo operacijos apibrėžimą turime: 0 = 0 x. Tačiau ši lygybė galioja bet koks skaičius x, kas turėjo būti įrodyta.

3 atvejis

0 0 - bet koks skaičius.

tikrai,

Sprendimas. Apsvarstykite tris pagrindinius atvejus:

1) x = 0 – ši reikšmė šios lygties netenkina

(Kodėl?).

2) kada x> 0 gauname: x/x = 1, t.y. 1 = 1, iš kur seka,

ką x- bet koks skaičius; bet atsižvelgiant į tai

Mūsų atvejis x> 0, atsakymas yrax > 0 ;

3) kada x < 0 получаем: – x/x= 1, t.y. e . –1 = 1, todėl

Šiuo atveju sprendimo nėra.

Šiuo būdu, x > 0.

Pamokos pradžioje apžvelgsime pagrindines kvadratinių šaknų savybes, o tada pažvelgsime į keletą sudėtingų kvadratinių šaknų turinčių išraiškų supaprastinimo pavyzdžių.

Tema:Funkcija. Kvadratinės šaknies savybės

Pamoka:Sudėtingesnių išraiškų su šaknimis konvertavimas ir supaprastinimas

1. Kvadratinių šaknų savybių kartojimas

Trumpai pakartokime teoriją ir prisiminkime pagrindines kvadratinių šaknų savybes.

Kvadratinių šaknų savybės:

1. , vadinasi, ;

3. ;

4. .

2. Posakių su šaknimis supaprastinimo pavyzdžiai

Pereikime prie šių savybių naudojimo pavyzdžių.

1 pavyzdys: supaprastinkite išraišką .

Sprendimas. Kad būtų paprasčiau, skaičius 120 turi būti išskaidytas į pirminius veiksnius:

Sumos kvadratą atidarysime pagal atitinkamą formulę:

2 pavyzdys: supaprastinkite išraišką .

Sprendimas. Atsižvelgiame į tai, kad ši išraiška neturi prasmės visoms galimoms kintamojo reikšmėms, nes šioje išraiškoje yra kvadratinių šaknų ir trupmenų, o tai lemia priimtinų verčių diapazono „susiaurėjimą“. ODZ: ().

Išraišką skliausteliuose perkeliame į bendrą vardiklį ir paskutinės trupmenos skaitiklį įrašome kaip kvadratų skirtumą:

At.

Atsakymas. adresu.

3 pavyzdys: supaprastinkite išraišką .

Sprendimas. Matyti, kad antrasis skaitiklio skliaustas yra nepatogios formos ir jį reikia supaprastinti, pabandykime jį suskaidyti grupavimo metodu.

Kad galėtume išskirti bendrą veiksnį, supaprastinome šaknis, jas įvertindami. Pakeiskite gautą išraišką pradine trupmena:

Sumažinus trupmeną taikome kvadratų skirtumo formulę.

3. Iracionalumo atsikratymo pavyzdys

4 pavyzdys. Atsikratykite iracionalumo (šaknų) vardiklyje: a) ; b) .

Sprendimas. a) Siekiant atsikratyti neracionalumo vardiklyje, naudojamas standartinis trupmenos skaitiklio ir vardiklio dauginimo iš konjuguoto koeficiento su vardikliu metodas (ta pati išraiška, bet su priešingu ženklu). Tai daroma siekiant papildyti trupmenos vardiklį prie kvadratų skirtumo, o tai leidžia atsikratyti vardiklio šaknų. Padarykime tai mūsų atveju:

b) atlikti panašius veiksmus:

Atsakymas.; .

4. Pavyzdys, kaip įrodyti ir atrinkti pilną kvadratą kompleksiniame radikale

5 pavyzdys. Įrodykite lygybę .

Įrodymas. Naudokime kvadratinės šaknies apibrėžimą, iš kurio išplaukia, kad teisingos išraiškos kvadratas turi būti lygus šaknies išraiškai:

. Atverkime skliaustus pagal sumos kvadrato formulę:

, gauname teisingą lygtį.

Įrodyta.

6 pavyzdys. Supaprastinkite išraišką.

Sprendimas. Ši išraiška paprastai vadinama kompleksiniu radikalu (šaknis po šaknimi). Šiame pavyzdyje turite atspėti, kad pasirinktumėte visą kvadratą iš radikalios išraiškos. Norėdami tai padaryti, pažymime, kad iš šių dviejų terminų jis pretenduoja į dvigubo sandaugos vaidmenį skirtumo kvadrato formulėje (skirtumas, nes yra minusas). Parašykime jį tokio sandaugos forma: , tada , pretenduoja į vieną iš viso kvadrato sąlygų, o 1 atlieka antrojo vaidmenį.

Pakeiskime šią išraišką šaknimi.

Konvertuojant posakius su šaknimis ir galiomis, dažnai reikia pereiti nuo šaknų prie galių ir atvirkščiai. Šiame straipsnyje mes analizuosime, kaip tokie perėjimai atliekami, kas yra jų pagrindas ir kuriuose taškuose dažniausiai pasitaiko klaidų. Visa tai pateiksime būdingais pavyzdžiais su detalia sprendimų analize.

Puslapio naršymas.

Perėjimas nuo laipsnių su trupmeniniais rodikliais prie šaknų

Galimybę pereiti nuo laipsnio su trupmeniniu rodikliu į šaknį lemia pats laipsnio apibrėžimas. Prisiminkite, kaip jis nustatomas: teigiamo skaičiaus a laipsnis su trupmeniniu rodikliu m / n, kur m yra sveikas skaičius, o n yra natūralusis skaičius, vadinamas n-ąja m šaknimi, tai yra, kur a> 0, m∈Z, n∈ N. Panašiai apibrėžiama ir nulio trupmeninė galia , su vieninteliu skirtumu, kad šiuo atveju m jau laikomas ne sveikuoju skaičiumi, o natūraliu, todėl dalijimas iš nulio neįvyksta.

Taigi laipsnį visada galima pakeisti šaknimi. Pavyzdžiui, galite pereiti nuo iki , o laipsnį galima pakeisti šaknimi. Tačiau neturėtumėte pereiti nuo išraiškos prie šaknies, nes laipsnis iš pradžių neturi prasmės (neigiamų skaičių laipsnis nėra apibrėžtas), nepaisant to, kad šaknis turi prasmę.

Kaip matote, pereinant nuo skaičių galių prie šaknų nėra nieko sudėtingo. Panašiai atliekamas perėjimas prie laipsnių šaknų su trupmeniniais rodikliais, pagrįstas savavališkomis išraiškomis. Atkreipkite dėmesį, kad nurodytas perėjimas atliekamas naudojant pradinės išraiškos kintamųjų ODZ. Pavyzdžiui, išraiška visame ODZ kintamąjį x šiai išraiškai galima pakeisti šaknimi . Ir nuo laipsnio eiti į šaknį , toks pakeitimas vyksta bet kuriam kintamųjų x , y ir z rinkiniui iš pradinės išraiškos DPV.

Šaknų pakeitimas galiomis

Galimas ir atvirkštinis pakeitimas, tai yra, šaknų pakeitimas laipsniais trupmeniniais eksponentais. Jis taip pat pagrįstas lygybe, kuri šiuo atveju naudojama iš dešinės į kairę, tai yra, forma.

Kalbant apie teigiamą a, šis perėjimas yra akivaizdus. Pavyzdžiui, laipsnį galite pakeisti ir nuo šaknies pereiti prie laipsnio formos trupmeniniu rodikliu.

O neigiamam a lygybė neturi prasmės, bet šaknis gali turėti prasmės. Pavyzdžiui, šaknys turi prasmę, bet jų negalima pakeisti galiomis. Taigi ar jas apskritai galima paversti galios išraiškomis? Tai įmanoma, jei atliksime išankstines transformacijas, kurias sudaro perėjimas prie šaknų su neneigiamais skaičiais po jais, kurie vėliau pakeičiami laipsniais su trupmeniniais rodikliais. Parodykime, kas yra šios preliminarios transformacijos ir kaip jas atlikti.

Šaknies atveju galite atlikti šias transformacijas: . Ir kadangi 4 yra teigiamas skaičius, paskutinę šaknį galima pakeisti laipsniu. Ir antruoju atveju nustatant nelyginio laipsnio šaknį iš neigiamo skaičiaus−a (šiuo atveju a yra teigiama), kuri išreiškiama lygybe , leidžia šaknį pakeisti išraiška, kurioje dviejų kubinę šaknį jau galima pakeisti laipsniu, ir ji įgis formą .

Belieka išsiaiškinti, kaip šaknys, po kuriomis yra išsidėstę posakiai, pakeičiamos laipsniais, kurių pagrindu yra šios išraiškos. Čia neturėtumėte skubėti pakeisti tam tikra išraiška, kurią pažymėjome raide A. Paimkime pavyzdį, kad paaiškintume, ką tai reiškia. Šaknį norima pakeisti laipsniu, paremtu lygybe. Bet toks pakeitimas tinkamas tik tada, kai x−3≥0<0 ) она не подходит, так как формула не имеет смысла для отрицательных a . Если обратить внимание на ОДЗ, то несложно заметить ее сужение при переходе от выражения к выражению , а помните, что мы договорились не прибегать к преобразованиям, сужающим ОДЗ.

Dėl tokio netikslaus formulės taikymo dažnai atsiranda klaidų pereinant nuo šaknų prie galių. Pavyzdžiui, vadovėlyje duodama užduotis pateikti išraišką kaip laipsnį su racionaliuoju rodikliu ir pateikiamas atsakymas, kuris kelia klausimų, nes sąlygoje apribojimas b>0 nenustatytas. Ir vadovėlyje yra perėjimas nuo išraiškos , greičiausiai dėl šių neracionalios išraiškos transformacijų

į išraišką. Paskutinis perėjimas taip pat kelia klausimų, nes susiaurina ODZ.

Kyla logiškas klausimas: „Kaip teisinga pereiti nuo šaknies prie laipsnio visoms kintamųjų reikšmėms iš ODZ“? Šis pakeitimas pagrįstas šiais teiginiais:

Prieš pagrįsdami užfiksuotus rezultatus, pateikiame kelis jų panaudojimo pavyzdžius pereinant nuo šaknų prie galių. Pirmiausia grįžkime prie išraiškos. Jį reikėjo pakeisti ne , o (šiuo atveju m=2 yra lyginis sveikas skaičius, n=3 yra natūralusis skaičius). Kitas pavyzdys: .

Dabar žadėtas rezultatų pagrindimas.

Kai m yra nelyginis sveikasis skaičius, o n yra teigiamas sveikasis skaičius, tada bet kurios kintamųjų rinkinio DPV, skirto išraiškai, išraiškos A reikšmė yra teigiama (jei m<0 ) или неотрицательно (если m>0). Štai kodėl, .

Pereikime prie antrojo rezultato. Tegu m yra teigiamas nelyginis sveikasis skaičius, o n – nelyginis natūralusis skaičius. Visoms kintamųjų reikšmėms iš ODZ, kurių išraiškos A reikšmė nėra neigiama, , ir kuriai jis yra neigiamas,

Šis rezultatas panašiai įrodomas neigiamiems ir nelyginiams sveikiesiems skaičiams m ir natūraliems nelyginiams n . Visoms kintamųjų reikšmėms iš ODZ, kurių išraiškos A reikšmė yra teigiama, , ir kuriai jis yra neigiamas,

Pagaliau paskutinis rezultatas. Tegu m lyginis sveikasis skaičius, n bet koks natūralusis skaičius. Visoms kintamųjų reikšmėms iš ODZ, kurių išraiškos A reikšmė yra teigiama (jei m<0 ) или неотрицательно (если m>0 ), . Ir kuriai tai yra neigiama, . Taigi, jei m yra lyginis sveikasis skaičius, n yra bet koks natūralusis skaičius, tai bet kuriai DPV kintamųjų verčių rinkiniui išraiškai jis gali būti pakeistas .

Bibliografija.

1. Algebra ir analizės pradžia: Proc. 10-11 ląstelių. bendrojo išsilavinimo institucijos / A. N. Kolmogorovas, A. M. Abramovas, Yu. P. Dudnicynas ir kt.; Red. A. N. Kolmogorova.- 14 leid.- M.: Švietimas, 2004.- 384 p.: iliustr.- ISBN 5-09-013651-3.
2. Algebra ir matematinės analizės pradžia. 11 klasė: vadovėlis. bendrajam lavinimui institucijos: pagrindinės ir profilio. lygiai / [Yu. M. Koliaginas, M. V. Tkačiova, N. E. Fedorova, M. I. Šabuninas]; red. A. B. Žižčenka. - M .: Švietimas, 2009. - 336 p.: Ill. - ISBN 979-5-09-016551-8.

Sveikiname: šiandien analizuosime šaknis – vieną labiausiai jaudinančių 8 klasės temų. :)

Daugelis žmonių susipainioja dėl šaknų ne dėl to, kad jos yra sudėtingos (o tai sudėtinga – pora apibrėžimų ir dar pora savybių), o todėl, kad daugumoje mokyklinių vadovėlių šaknys apibrėžiamos tokiais laukiniais simboliais, kuriuos gali tik patys vadovėlių autoriai. suprask šį rašymą. Ir net tada tik su buteliu gero viskio. :)

Todėl dabar pateiksiu teisingiausią ir kompetentingiausią šaknies apibrėžimą - vienintelį, kurį tikrai reikia atsiminti. Ir tik tada paaiškinsiu: kodėl viso to reikia ir kaip tai pritaikyti praktikoje.

Tačiau pirmiausia atsiminkite vieną svarbų dalyką, kurį dėl kokių nors priežasčių daugelis vadovėlių rengėjų „pamiršta“:

Šaknys gali būti lyginio laipsnio (mūsų mėgstamiausias $\sqrt(a)$, taip pat bet koks $\sqrt(a)$ ir net $\sqrt(a)$) ir nelyginio laipsnio (bet koks $\sqrt(a)$ , $\ sqrt(a)$ ir tt). Ir nelyginio laipsnio šaknies apibrėžimas šiek tiek skiriasi nuo lyginio.

Čia, šitame sušiktame „kiek kitaip“, slepiasi, ko gero, 95% visų klaidų ir nesusipratimų, susijusių su šaknimis. Taigi kartą ir visiems laikams išsiaiškinkime terminiją:

Apibrėžimas. Net šaknis n nuo skaičiaus $a$ yra bet koks ne neigiamas toks skaičius $b$, kad $((b)^(n))=a$. O nelyginio laipsnio šaknis iš to paties skaičiaus $a$ paprastai yra bet koks skaičius $b$, kuriam galioja ta pati lygybė: $((b)^(n))=a$.

Bet kokiu atveju šaknis žymima taip:

\(a)\]

Skaičius $n$ tokiame žymėjime vadinamas šaknies eksponentu, o skaičius $a$ – radikaliąja išraiška. Konkrečiai, už $n=2$ gauname „mėgstamiausią“ kvadratinę šaknį (beje, tai lyginio laipsnio šaknis), o už $n=3$ gauname kubinę šaknį (nelyginį laipsnį), kuri taip pat dažnai randama uždaviniuose ir lygtyse.

Pavyzdžiai. Klasikiniai kvadratinių šaknų pavyzdžiai:

\[\begin(lygiuoti) & \sqrt(4)=2; \\ & \sqrt(81)=9; \\ & \sqrt(256)=16. \\ \end(lygiuoti)\]

Beje, $\sqrt(0)=0$ ir $\sqrt(1)=1$. Tai gana logiška, nes $((0)^(2))=0$ ir $((1)^(2))=1$.

Kubinės šaknys taip pat dažnos - nebijokite jų:

\[\begin(lygiuoti) & \sqrt(27)=3; \\ & \sqrt(-64)=-4; \\ & \sqrt(343)=7. \\ \end(lygiuoti)\]

Na, pora „egzotiškų pavyzdžių“:

\[\begin(lygiuoti) & \sqrt(81)=3; \\ & \sqrt(-32)=-2. \\ \end(lygiuoti)\]

Jei nesuprantate, kuo skiriasi lyginis ir nelyginis laipsnis, dar kartą perskaitykite apibrėžimą. Tai labai svarbu!

Tuo tarpu mes apsvarstysime vieną nemalonią šaknų savybę, dėl kurios reikėjo įvesti atskirą lyginių ir nelyginių eksponentų apibrėžimą.

Kam mums apskritai reikalingos šaknys?

Perskaitę apibrėžimą, daugelis mokinių paklaus: „Ką rūkė matematikai, kai tai sugalvojo? Ir iš tikrųjų: kam mums reikalingos visos šios šaknys?

Norėdami atsakyti į šį klausimą, trumpam grįžkime į pradinę mokyklą. Prisiminkite: tais tolimais laikais, kai medžiai buvo žalesni, o koldūnai skanesni, mūsų pagrindinis rūpestis buvo teisingai padauginti skaičius. Na, kažkas tokio „penki iš penkių – dvidešimt penki“, tai ir viskas. Bet juk skaičius galima padauginti ne poromis, o trynukais, keturiais ir apskritai ištisomis aibėmis:

\[\begin(lygiuoti) & 5\cdot 5=25; \\ & 5\cdot 5\cdot 5=125; \\ & 5\cdot 5\cdot 5\cdot 5 = 625; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5=3125; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5=15\ 625. \end (lygiuoti)\]

Tačiau tai ne esmė. Gudrybė kitokia: matematikai yra tinginiai, todėl dešimties penketukų dauginimą jie turėjo užrašyti taip:

Taigi jie sugalvojo laipsnius. Kodėl faktorių skaičiaus neįrašius kaip viršutinį indeksą, o ne kaip ilgą eilutę? Kaip šis:

Tai labai patogu! Visi skaičiavimai sumažinami kelis kartus, ir jūs negalite išleisti krūvos pergamentinių sąsiuvinių lapų, kad užsirašytumėte 5 183 . Toks įrašas buvo vadinamas skaičiaus laipsniu, jame buvo rasta krūva savybių, tačiau laimė pasirodė trumpalaikė.

Po grandiozinio išgertuvės, kuri buvo surengta kaip tik dėl laipsnių „atradimo“, kažkoks ypač akmenuotas matematikas staiga paklausė: „O jeigu žinome skaičiaus laipsnį, bet nežinome paties skaičiaus? Iš tiesų, jei žinome, kad, pavyzdžiui, tam tikras skaičius $b$ duoda 243 iki 5 laipsnio, kaip galime atspėti, kam yra lygus pats skaičius $b$?

Ši problema pasirodė daug globalesnė, nei gali pasirodyti iš pirmo žvilgsnio. Nes paaiškėjo, kad daugumai „gatavų“ laipsnių tokių „pradinių“ skaičių nėra. Spręskite patys:

\[\begin(align) & ((b)^(3))=27\Rightarrow b=3\cdot 3\cdot 3\Rightarrow b=3; \\ & ((b)^(3))=64\RightArrow b=4\cdot 4\cdot 4\RightArrow b=4. \\ \end(lygiuoti)\]

O kas, jei $((b)^(3)) = 50 $? Pasirodo, reikia rasti tam tikrą skaičių, kurį padauginus iš savęs tris kartus, gautume 50. Bet kas tai yra skaičius? Jis aiškiai didesnis nei 3, nes 3 3 = 27< 50. С тем же успехом оно меньше 4, поскольку 4 3 = 64 >50. T.y. šis skaičius yra kažkur tarp trijų ir keturių, bet kam jis lygus - FIG jūs suprasite.

Būtent todėl matematikai sugalvojo $n$-ąją šaknis. Štai kodėl buvo pristatyta radikali piktograma $\sqrt(*)$. Pažymėti tą patį skaičių $b$, kuris pagal nurodytą laipsnį duos mums anksčiau žinomą reikšmę

\[\sqrt[n](a)=b\Rodyklė dešinėn ((b)^(n))=a\]

Nesiginčiju: dažnai šios šaknys yra lengvai svarstomos – aukščiau matėme keletą tokių pavyzdžių. Tačiau daugeliu atvejų, jei galvojate apie savavališką skaičių ir bandote iš jo išgauti savavališko laipsnio šaknį, jūsų laukia žiaurus bėdas.

Kas ten! Netgi paprasčiausias ir žinomiausias $\sqrt(2)$ negali būti pavaizduotas mums įprasta forma – kaip sveikasis skaičius arba trupmena. Ir jei įvesite šį skaičių į skaičiuotuvą, pamatysite tai:

\[\sqrt(2)=1,414213562...\]

Kaip matote, po kablelio yra begalinė skaičių seka, kuri nepaklūsta jokiai logikai. Žinoma, galite suapvalinti šį skaičių, kad greitai palygintumėte su kitais skaičiais. Pavyzdžiui:

\[\sqrt(2)=1,4142...\apytiksliai 1,4 \lt 1,5\]

Arba štai kitas pavyzdys:

\[\sqrt(3)=1,73205...\apytiksliai 1,7 \gt 1,5\]

Tačiau visi šie apvalinimai, pirma, yra gana grubūs; ir antra, reikia mokėti dirbti ir su apytiksliais dydžiais, antraip gali pasigauti krūvą neakivaizdžių klaidų (beje, lyginimo ir apvalinimo įgūdžiai būtinai tikrinami profilio egzamine).

Todėl rimtoje matematikoje negalima išsiversti be šaknų - jie yra vienodi visų realiųjų skaičių $\mathbb(R)$ aibės atstovai, kaip ir trupmenos bei sveikieji skaičiai, kuriuos mes jau seniai žinome.

Neįmanoma pateikti šaknies kaip formos $\frac(p)(q)$ trupmenos reiškia, kad ši šaknis nėra racionalus skaičius. Tokie skaičiai vadinami neracionaliais ir negali būti tiksliai pavaizduoti nebent naudojant radikalą ar kitas specialiai tam skirtas konstrukcijas (logaritmus, laipsnius, ribas ir pan.). Bet apie tai plačiau kitą kartą.

Apsvarstykite keletą pavyzdžių, kai po visų skaičiavimų atsakyme vis tiek liks neracionalūs skaičiai.

\[\begin(lygiuoti) & \sqrt(2+\sqrt(27))=\sqrt(2+3)=\sqrt(5)\apytiksliai 2 236... \\ & \sqrt(\sqrt(-32) ))=\sqrt(-2)\apytiksliai -1 2599... \\ \end(lygiuoti)\]

Natūralu, kad pagal šaknies išvaizdą beveik neįmanoma atspėti, kurie skaičiai bus po kablelio. Tačiau skaičiuoti galima ir skaičiuotuvu, tačiau net ir pažangiausia datos skaičiuoklė mums pateikia tik kelis pirmuosius neracionalaus skaičiaus skaitmenis. Todėl daug teisingiau atsakymus rašyti $\sqrt(5)$ ir $\sqrt(-2)$.

Tam jie buvo sugalvoti. Kad būtų lengviau užrašyti atsakymus.

Kodėl reikalingi du apibrėžimai?

Dėmesingas skaitytojas tikriausiai jau pastebėjo, kad visos pavyzdžiuose pateiktos kvadratinės šaknys paimtos iš teigiamų skaičių. Na, bent jau nuo nulio. Tačiau kubo šaknys ramiai išgaunamos iš absoliučiai bet kokio skaičiaus – net teigiamo, netgi neigiamo.

Kodėl tai vyksta? Pažvelkite į funkcijos $y=((x)^(2))$ grafiką:

Kvadratinės funkcijos grafikas pateikia dvi šaknis: teigiamą ir neigiamą

Pabandykime apskaičiuoti $\sqrt(4)$ naudodami šį grafiką. Tam grafike nubrėžiama horizontali linija $y=4$ (pažymėta raudonai), kuri kerta parabolę dviejuose taškuose: $((x)_(1))=2$ ir $((x) _(2)) = -2 $. Tai gana logiška, nes

Viskas aišku su pirmuoju skaičiumi - jis yra teigiamas, todėl tai yra šaknis:

Bet ką tada daryti su antruoju punktu? Ar 4 turi dvi šaknis vienu metu? Juk jei skaičių −2 padalinsime kvadratu, gausime ir 4. Kodėl tada neparašius $\sqrt(4)=-2$? O kodėl mokytojai į tokius įrašus žiūri taip, lyg norėtų tave suvalgyti? :)

Bėda ta, kad jei nebus keliamos papildomos sąlygos, tai ketvertukas turės dvi kvadratines šaknis – teigiamą ir neigiamą. Ir bet kuris teigiamas skaičius taip pat turės du iš jų. Bet neigiami skaičiai iš viso neturės šaknų - tai matyti iš to paties grafiko, nes parabolė niekada nenukrenta žemiau ašies y, t.y. nepriima neigiamų verčių.

Panaši problema iškyla visoms šaknims su lygiu eksponentu:

1. Griežtai kalbant, kiekvienas teigiamas skaičius turės dvi šaknis su lyginiu eksponentu $n$;
2. Iš neigiamų skaičių šaknis su net $n$ iš viso neišgaunama.

Štai kodėl lyginės šaknies $n$ apibrėžimas konkrečiai numato, kad atsakymas turi būti neneigiamas skaičius. Taip atsikratome dviprasmybių.

Tačiau nelyginiams $n$ tokios problemos nėra. Norėdami tai pamatyti, pažvelkime į funkcijos $y=((x)^(3))$ grafiką:

Kubinė parabolė įgyja bet kokią reikšmę, todėl kubo šaknį galima paimti iš bet kurio skaičiaus

Iš šio grafiko galima padaryti dvi išvadas:

1. Kubinės parabolės šakos, skirtingai nei įprastos, eina į begalybę abiem kryptimis – ir aukštyn, ir žemyn. Todėl, kad ir kokiame aukštyje nubrėžtume horizontalią liniją, ši linija tikrai susikirs su mūsų grafiku. Todėl kubo šaknį visada galima paimti absoliučiai iš bet kokio skaičiaus;
2. Be to, tokia sankryža visada bus unikali, todėl jums nereikės galvoti, kurį skaičių laikyti „teisinga“ šaknimi, o kurį – balą. Štai kodėl nelyginio laipsnio šaknų apibrėžimas yra paprastesnis nei lyginio (nėra neneigiamumo reikalavimo).

Gaila, kad daugumoje vadovėlių šie paprasti dalykai nepaaiškinami. Vietoj to, mūsų smegenys pradeda sklandyti su visomis aritmetinėmis šaknimis ir jų savybėmis.

Taip, aš nesiginčiju: kas yra aritmetinė šaknis – taip pat reikia žinoti. Ir apie tai išsamiai pakalbėsiu atskiroje pamokoje. Šiandien apie tai irgi pakalbėsime, nes be jos visi pamąstymai apie $n$-osios daugumos šaknis būtų neišsamūs.

Bet pirmiausia turite aiškiai suprasti apibrėžimą, kurį pateikiau aukščiau. Priešingu atveju dėl terminų gausos galvoje prasidės tokia netvarka, kad galiausiai išvis nieko nesuprasi.

Ir viskas, ką jums reikia suprasti, yra skirtumas tarp lyginių ir nelyginių skaičių. Todėl dar kartą surinksime viską, ką tikrai reikia žinoti apie šaknis:

1. Lyginė šaknis egzistuoja tik iš neneigiamo skaičiaus ir pati visada yra neneigiamas skaičius. Neigiamų skaičių tokia šaknis neapibrėžta.
2. Tačiau nelyginio laipsnio šaknis egzistuoja iš bet kurio skaičiaus ir pati gali būti bet koks skaičius: teigiamiems skaičiams jis yra teigiamas, o neigiamiems skaičiams, kaip rodo viršutinė riba, neigiama.

Ar tai sunku? Ne, tai nėra sunku. Aišku? Taip, tai akivaizdu! Todėl dabar šiek tiek pasipraktikuosime su skaičiavimais.

Pagrindinės savybės ir apribojimai

Šaknys turi daug keistų savybių ir apribojimų – tai bus atskira pamoka. Todėl dabar mes apsvarstysime tik svarbiausią „lustą“, kuris taikomas tik šaknims su lygiu eksponentu. Šią savybę užrašome formulės forma:

\[\sqrt(((x)^(2n)))=\left| x\right|\]

Kitaip tariant, jei skaičių padidinsime iki lyginės laipsnio, o iš to ištrauksime to paties laipsnio šaknį, gausime ne pradinį skaičių, o jo modulį. Tai paprasta teorema, kurią nesunku įrodyti (pakanka atskirai apsvarstyti neneigiamus $x$, o tada atskirai apsvarstyti neigiamus). Mokytojai apie tai nuolat kalba, tai pateikiama kiekviename mokykliniame vadovėlyje. Tačiau kai tik reikia išspręsti neracionalias lygtis (t. y. lygtis, kuriose yra radikalo ženklas), mokiniai kartu pamiršta šią formulę.

Norėdami išsamiai suprasti problemą, minutei pamirškime visas formules ir pabandykite suskaičiuoti du skaičius į priekį:

\[\sqrt(((3)^(4)))=?\quad \sqrt(((\left(-3 \right))^(4)))=?\]

Tai labai paprasti pavyzdžiai. Pirmąjį pavyzdį išspręs dauguma žmonių, bet antruoju – daugelis. Kad be problemų išspręstumėte tokius nešvarumus, visada apsvarstykite procedūrą:

1. Pirma, skaičius padidinamas iki ketvirtosios laipsnio. Na, tai kažkaip lengva. Bus gautas naujas skaičius, kurį galima rasti net daugybos lentelėje;
2. Ir dabar iš šio naujo skaičiaus reikia išgauti ketvirtojo laipsnio šaknį. Tie. nėra šaknų ir laipsnių „sumažinimo“ – tai nuoseklūs veiksmai.

Panagrinėkime pirmą išraišką: $\sqrt(((3)^(4)))$. Akivaizdu, kad pirmiausia turite apskaičiuoti išraišką po šaknimi:

\[((3)^(4))=3\ctaškas 3\ctaškas 3\ctaškas 3=81\]

Tada ištraukiame ketvirtąją skaičiaus 81 šaknį:

Dabar padarykime tą patį su antrąja išraiška. Pirmiausia skaičių −3 pakeliame iki ketvirtosios laipsnio, kuriam reikia jį padauginti iš savęs 4 kartus:

\[((\left(-3 \right))^(4))=\left(-3 \right)\cdot \left(-3 \right)\cdot \left(-3 \right)\cdot \ kairėje (-3 \right) = 81\]

Gavome teigiamą skaičių, nes bendras minusų skaičius gaminyje yra 4 vnt., ir jie visi vienas kitą panaikins (juk minusas prie minuso duoda pliusą). Tada dar kartą ištraukite šaknį:

Iš principo šios eilutės nebūtų galima parašyti, nes nenuostabu, kad atsakymas bus toks pat. Tie. tos pačios lygiosios galios lygi šaknis „sudegina“ minusus, ir šia prasme rezultatas nesiskiria nuo įprasto modulio:

\[\begin(align) & \sqrt(((3)^(4)))=\left| 3\right|=3; \\ & \sqrt(((\left(-3 \right))^(4)))=\left| -3 \dešinė|=3. \\ \end(lygiuoti)\]

Šie skaičiavimai gerai sutampa su lyginio laipsnio šaknies apibrėžimu: rezultatas visada yra neneigiamas, o radikalinis ženklas taip pat visada yra neneigiamas skaičius. Priešingu atveju šaknis nėra apibrėžta.

Pastaba dėl operacijų tvarkos

1. Žymėjimas $\sqrt(((a)^(2)))$ reiškia, kad iš pradžių skaičių $a$ paimame kvadratu, o tada paimame gautos reikšmės kvadratinę šaknį. Todėl galime būti tikri, kad neneigiamas skaičius visada yra po šaknies ženklu, nes $((a)^(2))\ge 0$ vis tiek;
2. Tačiau žymėjimas $((\left(\sqrt(a) \right))^(2))$, priešingai, reiškia, kad iš tam tikro skaičiaus $a$ pirmiausia ištraukiame šaknį ir tik po to rezultatą kvadratu. Todėl skaičius $a$ jokiu būdu negali būti neigiamas – tai privalomas reikalavimas, įtrauktas į apibrėžimą.

Taigi jokiu būdu nereikėtų neapgalvotai mažinti šaknų ir laipsnių, taip tariamai „supaprastinant“ pirminę išraišką. Nes jei po šaknimi yra neigiamas skaičius, o jo rodiklis lyginis, gausime daug problemų.

Tačiau visos šios problemos aktualios tik lygiems rodikliams.

Minuso ženklo pašalinimas iš po šaknies ženklo

Natūralu, kad šaknys su nelyginiais rodikliais taip pat turi savo bruožą, kurio iš principo lyginiams neegzistuoja. Būtent:

\[\sqrt(-a)=-\sqrt(a)\]

Trumpai tariant, iš po nelyginio laipsnio šaknų ženklo galite išimti minusą. Tai labai naudinga savybė, leidžianti „išmesti“ visus minusus:

\[\begin(lygiuoti) & \sqrt(-8)=-\sqrt(8)=-2; \\ & \sqrt(-27)\cdot \sqrt(-32)=-\sqrt(27)\cdot \left(-\sqrt(32) \right)= \\ & =\sqrt(27)\cdot \sqrt(32)= \\ & =3\cdot 2=6. \end(lygiuoti)\]

Ši paprasta savybė labai supaprastina daugelį skaičiavimų. Dabar jums nereikia jaudintis: o jei neigiama išraiška pateko po šaknimi, o laipsnis šaknyje pasirodė lygus? Užtenka visus minusus „išmesti“ už šaknų ribų, po to juos galima dauginti vienas iš kito, dalyti ir apskritai padaryti daug įtartinų dalykų, kurie „klasikinių“ šaknų atveju garantuotai prives mus prie klaidos. .

Ir čia pasirodo kitas apibrėžimas – tas pats, kuriuo dauguma mokyklų pradeda neracionalių posakių tyrimą. Ir be kurio mūsų samprotavimai būtų neišsamūs. Susitikti!

aritmetinė šaknis

Trumpam manykime, kad po šaknies ženklu gali būti tik teigiami skaičiai arba, kraštutiniais atvejais, nulis. Įvertinkime lyginius / nelyginius rodiklius, įvertinkime visus aukščiau pateiktus apibrėžimus – dirbsime tik su neneigiamais skaičiais. Kas tada?

Ir tada gauname aritmetinę šaknį – ji iš dalies susikerta su mūsų „standartiniais“ apibrėžimais, bet vis tiek skiriasi nuo jų.

Apibrėžimas. Neneigiamo skaičiaus $a$ $n$-ojo laipsnio aritmetinė šaknis yra neneigiamas skaičius $b$, kad $((b)^(n))=a$.

Kaip matote, mūsų nebedomina paritetas. Vietoj to atsirado naujas apribojimas: radikali išraiška dabar visada yra neneigiama, o pati šaknis taip pat yra neneigiama.

Norėdami geriau suprasti, kuo aritmetinė šaknis skiriasi nuo įprastos, pažvelkite į mums jau žinomus kvadratinės ir kubinės parabolės grafikus:

Šaknies paieškos sritis – neneigiami skaičiai

Kaip matote, nuo šiol mus domina tik tie grafikų fragmentai, kurie yra pirmajame koordinačių ketvirtyje – kur koordinatės $x$ ir $y$ yra teigiamos (arba bent jau nulis). Jums nebereikia žiūrėti į indikatorių, kad suprastumėte, ar mes turime teisę įšaknyti neigiamą skaičių, ar ne. Nes neigiami skaičiai iš esmės nebelaikomi.

Galite paklausti: „Na, kam mums reikia tokio kastruoto apibrėžimo? Arba: „Kodėl mes negalime susitvarkyti su aukščiau pateiktu standartiniu apibrėžimu?

Na, aš duosiu tik vieną savybę, dėl kurios naujas apibrėžimas tampa tinkamas. Pavyzdžiui, eksponentiškumo taisyklė:

\[\sqrt[n](a)=\sqrt(((a)^(k)))\]

Atkreipkite dėmesį: radikaliąją išraišką galime pakelti iki bet kokios laipsnio ir tuo pačiu padauginti šaknies eksponentą iš tos pačios laipsnio – ir rezultatas bus toks pat! Štai keletas pavyzdžių:

\[\begin(lygiuoti) & \sqrt(5)=\sqrt(((5)^(2)))=\sqrt(25) \\ & \sqrt(2)=\sqrt(((2)^ (4)))=\sqrt(16) \\ \end(lygiuoti)\]

Na, kas čia blogo? Kodėl negalėjome to padaryti anksčiau? Štai kodėl. Apsvarstykite paprastą išraišką: $\sqrt(-2)$ yra skaičius, kuris yra gana normalus mūsų klasikine prasme, bet visiškai nepriimtinas aritmetinės šaknies požiūriu. Pabandykime konvertuoti:

$\begin(align) & \sqrt(-2)=-\sqrt(2)=-\sqrt(((2)^(2)))=-\sqrt(4) \lt 0; \\ & \sqrt(-2)=\sqrt(((\left(-2 \right))^(2)))=\sqrt(4) \gt 0. \\ \end(lygiuoti)$

Kaip matote, pirmuoju atveju iš po radikalo išėmėme minusą (turime visas teises, nes rodiklis nelyginis), o antruoju panaudojome aukščiau pateiktą formulę. Tie. matematikos požiūriu viskas daroma pagal taisykles.

WTF?! Kaip tas pats skaičius gali būti teigiamas ir neigiamas? Negali būti. Tiesiog eksponencijos formulė, kuri puikiai tinka teigiamiems skaičiams ir nuliui, neigiamų skaičių atveju pradeda kelti visišką ereziją.

Čia, norėdami atsikratyti tokio neaiškumo, jie sugalvojo aritmetines šaknis. Jiems skirta atskira didelė pamoka, kurioje išsamiai aptariame visas jų savybes. Taigi dabar ties jais nesigilinsime – pamoka vis tiek pasirodė per ilga.

Algebrinė šaknis: norintiems sužinoti daugiau

Ilgai galvojau: padaryti šią temą atskira pastraipa ar ne. Galiausiai nusprendžiau čia išvykti. Ši medžiaga skirta tiems, kurie nori dar geriau suprasti šaknis – jau ne vidutiniame „mokykliniame“, o olimpiadai artimame lygyje.

Taigi: be „klasikinio“ skaičiaus $n$-ojo laipsnio šaknies apibrėžimo ir su juo susijusio padalijimo į lyginius ir nelyginius rodiklius, yra ir labiau „suaugusiųjų“ apibrėžimas, kuris nepriklauso nuo pariteto ir išvis kitų subtilybių. Tai vadinama algebrine šaknimi.

Apibrėžimas. Bet kurio $a$ algebrinė $n$-oji šaknis yra visų skaičių $b$ rinkinys, kad $((b)^(n))=a$. Tokioms šaknims nėra nusistovėjusio pavadinimo, todėl tiesiog uždėkite brūkšnį viršuje:

\[\overline(\sqrt[n](a))=\left\(b\left| b\in \mathbb(R);((b)^(n))=a \right. \right\) \]

Esminis skirtumas nuo standartinio apibrėžimo, pateikto pamokos pradžioje, yra tas, kad algebrinė šaknis yra ne konkretus skaičius, o aibė. Kadangi dirbame su tikraisiais skaičiais, šis rinkinys yra tik trijų tipų:

1. Tuščias komplektas. Atsiranda, kai reikia rasti lyginio laipsnio algebrinę šaknį iš neigiamo skaičiaus;
2. Rinkinys, susidedantis iš vieno elemento. Į šią kategoriją patenka visos nelyginių galių šaknys, taip pat lyginių galių šaknys nuo nulio;
3. Galiausiai rinkinyje gali būti du skaičiai – tie patys $((x)_(1))$ ir $((x)_(2))=-((x)_(1))$, kuriuos matėme diagramos kvadratinė funkcija. Atitinkamai, toks lygiavimas galimas tik iš teigiamo skaičiaus išimant lyginio laipsnio šaknį.

Paskutinis atvejis nusipelno išsamesnio svarstymo. Suskaičiuokime keletą pavyzdžių, kad suprastume skirtumą.

Pavyzdys. Apskaičiuokite išraiškas:

\[\overline(\sqrt(4));\quad \overline(\sqrt(-27));\quad \overline(\sqrt(-16)).\]

Sprendimas. Pirmoji išraiška paprasta:

\[\overline(\sqrt(4))=\left\( 2;-2 \right\)\]

Tai du skaičiai, kurie yra rinkinio dalis. Nes kiekvienas iš jų kvadratu duoda ketvertą.

\[\overline(\sqrt(-27))=\left\( -3 \right\)\]

Čia matome rinkinį, kurį sudaro tik vienas skaičius. Tai gana logiška, nes šaknies rodiklis yra nelyginis.

Galiausiai paskutinė išraiška:

\[\overline(\sqrt(-16))=\varnothing \]

Turime tuščią rinkinį. Nes nėra nė vieno realaus skaičiaus, kurį padidinus iki ketvirtosios (tai yra lyginės!) galios, gautume neigiamą skaičių −16.

Baigiamoji pastaba. Atkreipkite dėmesį: neatsitiktinai visur pažymėjau, kad dirbame su tikraisiais skaičiais. Kadangi yra ir kompleksinių skaičių - ten visiškai įmanoma suskaičiuoti $\sqrt(-16)$ ir daug kitų keistų dalykų.

Tačiau šiuolaikinėje mokyklinėje matematikos programoje sudėtingų skaičių beveik niekada nerandama. Daugumoje vadovėlių jie buvo praleisti, nes mūsų pareigūnai mano, kad ši tema „per sunkiai suprantama“.

Tai viskas. Kitoje pamokoje apžvelgsime visas pagrindines šaknų savybes ir pagaliau išmoksime supaprastinti neracionalias išraiškas. :)