Sa luam in considerare rezolvarea ecuaţiilor cu o variabilă de grad mai mare decât a doua.
Gradul ecuației P(x) = 0 este gradul polinomului P(x), adică. cea mai mare dintre puterile termenilor săi cu un coeficient diferit de zero.
Deci, de exemplu, ecuația (x 3 – 1) 2 + x 5 = x 6 – 2 are gradul al cincilea, deoarece în urma operaţiilor de deschidere a parantezelor şi aducere a unora asemănătoare se obţine ecuaţia echivalentă x 5 – 2x 3 + 3 = 0 de gradul al cincilea.
Să ne amintim regulile care vor fi necesare pentru a rezolva ecuații de grad mai mare decât doi.
Afirmații despre rădăcinile unui polinom și divizorii acestuia:
1. Un polinom de gradul al n-lea are un număr de rădăcini care nu depășește n, iar rădăcinile de multiplicitate m apar de exact de m ori.
2. Un polinom de grad impar are cel puțin o rădăcină reală.
3. Dacă α este rădăcina lui P(x), atunci P n (x) = (x – α) · Q n – 1 (x), unde Q n – 1 (x) este un polinom de grad (n – 1) .
4.
5. Polinomul redus cu coeficienți întregi nu poate avea rădăcini raționale fracționale.
6. Pentru un polinom de gradul trei
P 3 (x) = ax 3 + bx 2 + cx + d este posibil unul din două lucruri: fie este descompus în produsul a trei binoame
Р 3 (x) = а(х – α)(х – β)(х – γ), sau se descompune în produsul dintre un binom și un trinom pătrat Р 3 (x) = а(х – α)(х 2 + βх + γ ).
7. Orice polinom de gradul al patrulea poate fi extins în produsul a două trinoame pătrate.
8. Un polinom f(x) este divizibil cu un polinom g(x) fără rest dacă există un polinom q(x) astfel încât f(x) = g(x) · q(x). Pentru a împărți polinoamele, se folosește regula „divizării colțurilor”.
9. Pentru ca polinomul P(x) să fie divizibil cu un binom (x – c), este necesar și suficient ca numărul c să fie rădăcina lui P(x) (Corolarul teoremei lui Bezout).
10. Teorema lui Vieta: Dacă x 1, x 2, ..., x n sunt rădăcini reale ale polinomului
P(x) = a 0 x n + a 1 x n - 1 + ... + a n, atunci sunt valabile următoarele egalități:
x 1 + x 2 + … + x n = -a 1 /a 0,
x 1 x 2 + x 1 x 3 + … + x n – 1 x n = a 2 /a 0,
x 1 x 2 x 3 + … + x n – 2 x n – 1 x n = -a 3 / a 0,
x 1 · x 2 · x 3 · x n = (-1) n a n / a 0 .
Rezolvarea exemplelor
Exemplul 1.
Aflați restul diviziunii P(x) = x 3 + 2/3 x 2 – 1/9 prin (x – 1/3).
Soluţie.
Prin corolar teoremei lui Bezout: „Rămânul unui polinom împărțit la un binom (x – c) este egal cu valoarea polinomului lui c.” Să găsim P(1/3) = 0. Prin urmare, restul este 0 și numărul 1/3 este rădăcina polinomului.
Răspuns: R = 0.
Exemplul 2.
Împărțiți cu un „colț” 2x 3 + 3x 2 – 2x + 3 la (x + 2). Găsiți restul și coeficientul incomplet. 
Soluţie:
2x 3 + 3x 2 – 2x + 3| x + 2
2x 3 + 4 x 2 2x 2 – x
X 2 – 2 x
Răspuns: R = 3; coeficient: 2x 2 – x.
Metode de bază pentru rezolvarea ecuațiilor de grad superior
1. Introducerea unei noi variabile
Metoda de introducere a unei noi variabile este deja familiară din exemplul ecuațiilor biquadratice. Constă în faptul că pentru rezolvarea ecuației f(x) = 0 se introduce o nouă variabilă (substituție) t = x n sau t = g(x) și se exprimă f(x) prin t, obținându-se o nouă ecuație r (t). Apoi rezolvând ecuația r(t), se găsesc rădăcinile:
(t 1, t 2, …, t n). După aceasta, se obține o mulțime de n ecuații q(x) = t 1 , q(x) = t 2 , … , q(x) = t n, din care se găsesc rădăcinile ecuației inițiale.
Exemplul 1.
(x 2 + x + 1) 2 – 3x 2 – 3x – 1 = 0.
Soluţie:
(x 2 + x + 1) 2 – 3(x 2 + x) – 1 = 0.
(x 2 + x + 1) 2 – 3(x 2 + x + 1) + 3 – 1 = 0.
Înlocuire (x 2 + x + 1) = t.
t 2 – 3t + 2 = 0.
t 1 = 2, t 2 = 1. Substituție inversă:
x 2 + x + 1 = 2 sau x 2 + x + 1 = 1;
x 2 + x - 1 = 0 sau x 2 + x = 0;
Răspuns: Din prima ecuație: x 1, 2 = (-1 ± √5)/2, din a doua: 0 și -1.
2. Factorizarea prin grupare și formule de înmulțire prescurtate
De asemenea, baza acestei metode nu este nouă și constă în gruparea termenilor în așa fel încât fiecare grup să conțină un factor comun. Pentru a face acest lucru, uneori este necesar să folosiți câteva tehnici artificiale.
Exemplul 1.
x 4 – 3x 2 + 4x – 3 = 0.
Soluţie.
Să ne imaginăm - 3x 2 = -2x 2 – x 2 și grupați:
(x 4 – 2x 2) – (x 2 – 4x + 3) = 0.
(x 4 – 2x 2 +1 – 1) – (x 2 – 4x + 3 + 1 – 1) = 0.
(x 2 – 1) 2 – 1 – (x – 2) 2 + 1 = 0.
(x 2 – 1) 2 – (x – 2) 2 = 0.
(x 2 – 1 – x + 2)(x 2 – 1 + x - 2) = 0.
(x 2 – x + 1)(x 2 + x – 3) = 0.
x 2 – x + 1 = 0 sau x 2 + x – 3 = 0.
Răspuns: Nu există rădăcini în prima ecuație, din a doua: x 1, 2 = (-1 ± √13)/2.
3. Factorizarea prin metoda coeficienților nedeterminați
Esența metodei este că polinomul original este factorizat cu coeficienți necunoscuți. Folosind proprietatea că polinoamele sunt egale dacă coeficienții lor sunt egali la aceleași puteri, se găsesc coeficienții de expansiune necunoscuți.
Exemplul 1.
x 3 + 4x 2 + 5x + 2 = 0.
Soluţie.
Un polinom de gradul 3 poate fi extins în produsul factorilor liniari și pătratici.
x 3 + 4x 2 + 5x + 2 = (x – a)(x 2 + bx + c),
x 3 + 4x 2 + 5x + 2 = x 3 +bx 2 + cx – ax 2 – abx – ac,
x 3 + 4x 2 + 5x + 2 = x 3 + (b – a)x 2 + (cx – ab)x – ac.
După ce am rezolvat sistemul:
(b – a = 4,
(c – ab = 5,
(-ac = 2,
(a = -1,
(b = 3,
(c = 2, adică
x 3 + 4x 2 + 5x + 2 = (x + 1)(x 2 + 3x + 2).
Rădăcinile ecuației (x + 1)(x 2 + 3x + 2) = 0 sunt ușor de găsit.
Raspunsul 1; -2.
4. Metoda de selectare a unei rădăcini folosind coeficientul cel mai mare și liber

Metoda se bazează pe aplicarea teoremelor:
1) Fiecare rădăcină întreagă a unui polinom cu coeficienți întregi este un divizor al termenului liber.
2) Pentru ca fracția ireductibilă p/q (p este un număr întreg, q este un număr natural) să fie rădăcina unei ecuații cu coeficienți întregi, este necesar ca numărul p să fie un divizor întreg al termenului liber a 0, și q să fie un divizor natural al coeficientului principal.
Exemplul 1.
6x 3 + 7x 2 – 9x + 2 = 0.
Soluţie:
6: q = 1, 2, 3, 6.
Prin urmare, p/q = ±1, ±2, ±1/2, ±1/3, ±2/3, ±1/6.
După ce am găsit o rădăcină, de exemplu – 2, vom găsi alte rădăcini folosind diviziunea colțului, metoda coeficienților nedeterminați sau schema lui Horner.
Răspuns: -2; 1/2; 1/3.
Mai ai întrebări? Nu știi cum să rezolvi ecuații?
Pentru a obține ajutor de la un tutor, înregistrați-vă.
Prima lecție este gratuită!
site-ul web, atunci când copiați materialul integral sau parțial, este necesar un link către sursă.
SCHEMA cornului
ÎN REZOLVAREA ECUATIILOR CU PARAMETRI
DIN GRUPA „C” ÎN PREGĂTIREA EXAMENULUI DE STAT Unificat
Kazantseva Lyudmila Viktorovna
profesor de matematică la MBOU „Școala secundară Uyarskaya nr. 3”
La orele opționale, este necesar să se extindă gama de cunoștințe existente prin rezolvarea sarcinilor de complexitate crescută a grupei „C”.
Această lucrare acoperă unele dintre problemele discutate în clasele suplimentare.
Este recomandabil să introduceți schema lui Horner după ce ați studiat tema „Diviziunea unui polinom cu un polinom”. Acest material vă permite să rezolvați ecuații de ordin superior nu prin gruparea polinoamelor, ci într-un mod mai rațional, care economisește timp.
Planul lecției.
Lectia 1.
1. Explicarea materialului teoretic.
2. Rezolvarea exemplelor a B C D).
Lectia 2.
1. Rezolvarea ecuațiilor a B C D).
2. Găsirea rădăcinilor raționale ale unui polinom
Aplicarea schemei lui Horner în rezolvarea ecuațiilor cu parametri.
Lecția 3.
Sarcini a B C).
Lecția 4.
1. Sarcini d), e), f), g), h).
Rezolvarea ecuațiilor de grade superioare.
Schema lui Horner.
Teorema : Fie fracția ireductibilă rădăcina ecuației
A o X n + A 1 X n-1 + … + a n-1 X 1 + a n = 0
cu coeficienți întregi. Apoi numărul R este divizorul coeficientului principal A O .
Consecinţă: Orice rădăcină întreagă a unei ecuații cu coeficienți întregi este un divizor al termenului său liber.
Consecinţă: Dacă coeficientul principal al unei ecuații cu coeficienți întregi este egal cu 1 , atunci toate rădăcinile raționale, dacă există, sunt numere întregi.
Exemplul 1. 2x 3 – 7x 2 + 5x – 1 = 0
Fie fracția ireductibilă rădăcina ecuației, atunciR este un divizor al unui număr1:±1
q este divizorul termenului principal: ± 1; ± 2
Rădăcinile raționale ale ecuației trebuie căutate printre numerele:± 1; ± .
f(1) = 2 – 7 + 5 – 1 = – 1 ≠ 0
f(–1) = –2 – 7 – 5 – 1 ≠ 0
f() = – + – 1 = – +  – = 0
– = 0
Rădăcina este numărul .
Împărțirea unui polinom P(x) = a O X P + A 1 X n -1 + … + A n prin binom ( x – £) Este convenabil să efectuați conform schemei lui Horner.
Să notăm coeficientul incomplet P(x) pe ( x – £) prin Q (X ) = b o X n -1 + b 1 X n -2 + … b n -1 ,
iar restul prin b n
P(x) =Q (X ) (X – £) + b n , atunci identitatea este valabilă
A O X P + a 1 X n-1 + … + a n = (b o X n-1 + … + b n-1 ) (x – £) +b n
Q (X ) este un polinom al cărui grad este 1 sub gradul polinomului original. Coeficienți polinomi Q (X ) sunt determinate după schema lui Horner.
și despre
a 1
a 2
un n-1
un n
b o = a o
b 1 = A 1 + £· b o
b 2 = A 2 + £· b 1
b n-1 = a n-1 + £· b n-2
b n = a n + £· b n-1
În prima linie a acestui tabel scrieți coeficienții polinomului P(x).
Dacă lipsește un anumit grad al unei variabile, atunci este scrisă în celula corespunzătoare a tabelului 0.
Coeficientul principal al coeficientului este egal cu coeficientul principal al dividendului ( A O = b o ). Dacă £ este rădăcina polinomului, apoi în ultima celulă obținem 0.
Exemplul 2. Factorizați cu coeficienți întregi
P(x) = 2x 4 – 7x 3 – 3x 2 + 5x – 1
± 1.
Se potrivește - 1.
Ne împărțim P(x) pe (x + 1)
2
– 7
– 3
5
– 1
– 1
2
– 9
6
– 1
0
2x 4 – 7x 3 – 3x 2 + 5x – 1 = (x + 1) (2x 3 – 9x 2 + 6x – 1)
Căutăm rădăcini întregi printre termenii liberi: ± 1
Întrucât termenul conducător este egal cu 1, atunci rădăcinile pot fi numere fracționale: – ; .
Se potrivește .
2
– 9
6
– 1
2
– 8
2
0
2x 3 – 9x 2 + 6x – 1 = (x – ) (2x 2 – 8x + 2) = (2x – 1) (x 2 – 4x + 1)
Trinom X 2 – 4x + 1 nu poate fi factorizat în factori cu coeficienți întregi.
Exercițiu:
1. Factorizați cu coeficienți întregi:
A) X 3 – 2x 2 – 5x + 6
q: ± 1;
p: ± 1; ± 2; ± 3; ± 6
:± 1; ± 2; ± 3; ± 6
Găsirea rădăcinilor raționale ale unui polinom f (1) = 1 – 2 – 5 + 6 = 0
x = 1
1
– 2
– 5
6
1
1
– 1
– 6
0
x 3 – 2x 2 – 5x + 6 = (x – 1) (x 2 – x – 6) = (x – 1) (x – 3) (x + 2)
Să determinăm rădăcinile ecuației pătratice
x 2 – x – 6 = 0
x = 3; x = – 2
b) 2x 3 + 5x 2 + x – 2
p: ± 1; ± 2
q: ± 1; ± 2
:± 1; ± 2; ±
Să găsim rădăcinile unui polinom de gradul trei
f (1) = 2 + 5 + 1 – 2 ≠ 0
f (–1) = – 2 + 5 – 1 – 2 = 0
Una dintre rădăcinile ecuației x = – 1
2
5
1
– 2
– 1
2
3
– 2
0
2x 3 + 5x 2 + x – 2 = (x + 1) (2x 2 + 3x – 2) = (x + 1) (x + 2) (2x – 1)
Să extindem trinomul pătratic 2x 2 + 3x – 2 prin multiplicatori
2x 2 + 3x – 2 = 2 (x + 2) (x – )
D = 9 + 16 = 25
x 1 = – 2; x 2 =
V) X 3 – 3x 2 + x + 1
p: ± 1
q:±1
:± 1
f (1) = 1 – 3 + 1 – 1 = 0
Una dintre rădăcinile unui polinom de gradul trei este x = 1
1
– 3
1
1
1
1
– 2
– 1
0
x 3 – 3x 2 + x + 1 = (x – 1) (x 2 – 2x – 1)
Să găsim rădăcinile ecuației X 2 – 2х – 1 = 0
D= 4 + 4 = 8
x 1 = 1 – 
x 2 = 1 + 
x 3 – 3x 2 + x + 1 = (x – 1) (x – 1 +  ) (x – 1 –
) (x – 1 –  )
)
G) X 3 – 2x – 1
p: ± 1
q:±1
:± 1
Să determinăm rădăcinile polinomului
f (1) = 1 – 2 – 1 = – 2
f (–1) = – 1 + 2 – 1 = 0
Prima rădăcină x = – 1
1
0
– 2
– 1
– 1
1
– 1
– 1
0
x 3 – 2x – 1 = (x + 1) (x 2 – x – 1)
x 2 – x – 1 = 0
D = 1 + 4 = 5
x 1,2 = 
x 3 – 2x – 1 = (x + 1) (x –  ) (X -
) (X -  )
)
2. Rezolvați ecuația:
A) X 3 – 5x + 4 = 0
Să determinăm rădăcinile unui polinom de gradul trei
:± 1; ± 2; ± 4
f (1) = 1 – 5 + 4 = 0
Una dintre rădăcini este x = 1
1
0
– 5
4
1
1
1
– 4
0
x 3 – 5x + 4 = 0
(x – 1) (x 2 + x – 4) = 0
X 2 + x – 4 = 0
D = 1 + 16 = 17
x 1 =  ; X 2
=
; X 2
= 
Răspuns: 1;  ;
; 
b) X 3 – 8x 2 + 40 = 0
Să determinăm rădăcinile unui polinom de gradul trei.
:± 1; ± 2; ± 4; ± 5; ± 8; ± 10; ± 20; ± 40
f (1) ≠ 0
f (–1) ≠ 0
f (–2) = – 8 – 32 + 40 = 0
Una dintre rădăcini este x = – 2
1
– 8
0
40
– 2
1
– 10
20
0
Să factorizăm polinomul de gradul trei.
x 3 – 8x 2 + 40 = (x + 2) (x 2 – 10x + 20)
Să găsim rădăcinile ecuației pătratice X 2 – 10x + 20 = 0
D = 100 – 80 = 20
x 1 = 5 –  ; X 2
= 5 +
; X 2
= 5 + 
Răspuns: – 2; 5 –  ; 5 +
; 5 + 
V) X 3 – 5x 2 + 3x + 1 = 0
Căutăm rădăcini întregi printre divizorii termenului liber: ± 1
f (–1) = – 1 – 5 – 3 + 1 ≠ 0
f (1) = 1 – 5 + 3 + 1 = 0
Se potrivește x = 1
1
– 5
3
1
1
1
– 4
– 1
0
x 3 – 5x 2 + 3x + 1 = 0
(x – 1) (x 2 – 4x – 1) = 0
Determinarea rădăcinilor unei ecuații pătratice X 2 – 4x – 1 = 0
D=20
x = 2 +  ; x = 2 –
; x = 2 – 
Răspuns: 2 –  ; 1; 2 +
; 1; 2 + 
G) 2x 4 – 5x 3 + 5x 2 – 2 = 0
p: ± 1; ± 2
q: ± 1; ± 2
:± 1; ± 2; ±
f (1) = 2 – 5 + 5 – 2 = 0
Una dintre rădăcinile ecuației x = 1
2
– 5
5
0
– 2
1
2
– 3
2
2
0
2x 4 – 5x 3 + 5x 2 – 2 = 0
(x – 1) (2x 3 – 3x 2 + 2x + 2) = 0
Folosind aceeași schemă, găsim rădăcinile ecuației de gradul trei.
2x 3 – 3x 2 + 2x + 2 = 0
p: ± 1; ± 2
q: ± 1; ± 2
:± 1; ± 2; ±
f (1) = 2 – 3 + 2 + 2 ≠ 0
f (–1) = – 2 – 3 – 2 + 2 ≠ 0
f (2) = 16 – 12 + 4 + 2 ≠ 0
f (–2) = – 16 – 12 – 4 + 2 ≠ 0
f() = – + 1 + 2 ≠ 0
f(–) = – – – 1 + 2 ≠ 0
Următoarea rădăcină a ecuațieix = –
2
– 3
2
2
2
– 4
4
0
2x 3 – 3x 2 + 2x + 2 = 0
(x + ) (2x 2 – 4x + 4) = 0
Să determinăm rădăcinile ecuației pătratice 2x 2 – 4x + 4 = 0
x 2 – 2x + 2 = 0
D = – 4< 0
Prin urmare, rădăcinile ecuației originale de gradul patru sunt
1 și –
Răspuns: –; 1
3. Aflați rădăcinile raționale ale polinomului
A) X 4 – 2x 3 – 8x 2 + 13x – 24
q:±1
:± 1; ± 2; ± 3; ± 4; ± 6; ± 8; ± 12; ± 24
Să selectăm una dintre rădăcinile polinomului de gradul al patrulea:
f (1) = 1 – 2 – 8 + 13 – 24 ≠ 0
f (–1) = 1 + 2 – 8 – 13 – 24 ≠ 0
f (2) = 16 – 16 – 32 + 26 – 24 ≠ 0
f (–2) = 16 + 16 – 72 – 24 ≠ 0
f (–3) = 81 + 54 – 72 – 39 – 24 = 0
Una dintre rădăcinile polinomului X 0= – 3.
x 4 – 2x 3 – 8x 2 + 13x – 24 = (x + 3) (x 3 – 5x 2 + 7x + 8)
Să găsim rădăcinile raționale ale polinomului
x 3 – 5x 2 + 7x + 8
p: ± 1; ± 2; ± 4; ± 8
q:±1
f (1) = 1 – 5 + 7 + 8 ≠ 0
f (–1) = – 1 – 5 – 7 – 8 ≠ 0
f (2) = 8 – 20 + 14 + 8 ≠ 0
f (–2) = – 8 – 20 – 14 + 8 ≠ 0
f (–4) = 64 – 90 – 28 + 8 ≠ 0
f (4) ≠ 0
f (–8) ≠ 0
f (8) ≠ 0
Pe langa numarul X 0 = – 3 nu există alte rădăcini raţionale.
b) X 4 – 2x 3 – 13x 2 – 38х – 24
p: ± 1; ± 2; ± 3; ± 4; ± 6; ± 8; ± 12; ± 24
q:±1
f (1) = 1 + 2 – 13 – 38 – 24 ≠ 0
f (–1) = 1 – 2 – 13 + 38 – 24 = 39 – 39 = 0, acesta este x = – 1 rădăcina unui polinom
1
2
– 13
– 38
– 24
– 1
1
1
– 14
– 24
0
x 4 – 2x 3 – 13x 2 – 38x – 24 = (x + 1) (x 3 – x 2 – 14x – 24)
Să determinăm rădăcinile unui polinom de gradul trei X 3 - X 2 – 14х – 24
p: ± 1; ± 2; ± 3; ± 4; ± 6; ± 8; ± 12; ± 24
q:±1
f (1) = – 1 + 1 + 14 – 24 ≠ 0
f (–1) = 1 + 1 – 14 – 24 ≠ 0
f (2) = 8 + 4 – 28 – 24 ≠ 0
f (–2) = – 8 + 4 + 28 – 24 ≠ 0
Deci, a doua rădăcină a polinomului x = – 2
1
1
– 14
– 24
– 2
1
– 1
– 12
0
x 4 – 2x 3 – 13x 2 – 38x – 24 = (x + 1) (x 2 + 2) (x 2 – x – 12) =
= (x + 1) (x + 2) (x + 3) (x – 4)
Răspuns: – 3; – 2; – 1; 4
Aplicarea schemei lui Horner în rezolvarea ecuațiilor cu un parametru.
Găsiți cea mai mare valoare întreagă a parametrului A, la care ecuaţia f (x) = 0 are trei rădăcini diferite, dintre care una X 0 .
A) f (x) = x 3 + 8x 2 +ah+b , X 0 = – 3
Deci una dintre rădăcini X 0 = – 3 , atunci conform schemei lui Horner avem:
1
8
A
b
– 3
1
5
– 15 + a
0
0 = – 3 (– 15 + a) + b
0 = 45 – 3a + b
b = 3a – 45
x 3 + 8x 2 + ax + b = (x + 3) (x 2 + 5x + (a – 15))
Ecuația X 2 + 5x + (a – 15) = 0 D > 0
A = 1; b = 5; c = (a – 15),
D = b 2 – 4ac = 25 – 4 (a – 15) = 25 + 60 – 4a > 0,
85 – 4a > 0;
4a< 85;
A< 21
Cea mai mare valoare a parametrului întreg A, la care ecuaţia
f (x) = 0 are trei rădăcini a = 21
Răspuns: 21.
b) f(x) = x 3 – 2x 2 + ax + b, x 0 = – 1
Din moment ce una dintre rădăcini X 0= – 1, apoi conform schemei lui Horner avem
1
– 2
A
b
– 1
1
– 3
3 + a
0
x 3 – 2x 2 + ax + b = (x + 1) (x 2 – 3x + (3 + a))
Ecuația X 2 – 3 X + (3 + A ) = 0 trebuie să aibă două rădăcini. Acest lucru se face doar când D > 0
a = 1; b = – 3; c = (3 + a),
D = b 2 – 4ac = 9 – 4 (3 + a) = 9 – 12 – 4a = – 3 – 4a > 0,
– 3 – 4a > 0;
– 4a< 3;
A < –
Cea mai mare valoare a = – 1 a = 40
Răspuns: a = 40
G) f(x) = x 3 – 11x 2 + ax + b, x 0 = 4
Din moment ce una dintre rădăcini X 0 = 4 , apoi conform schemei lui Horner avem
1
– 11
A
b
4
1
– 7
– 28 + a
0
x 3 – 11x 2 + ax + b = (x – 4) (x 2 – 7x + (a – 28))
f (X ) = 0, Dacă x = 4 sau X 2 – 7 X + (A – 28) = 0
D > 0, acesta este
D = b 2 – 4ac = 49 – 4 (a – 28) = 49 + 112 – 4a = 161 – 4a >0,
161 – 4a > 0;
– 4a< – 161; f X 0 = – 5 , apoi conform schemei lui Horner avem
1
13
A
b
– 5
1
8
– 40 + a
0
x 3 + 13x 2 + ax + b = (x +5) (x 2 +8x + (a – 40))
f (X ) = 0, Dacă x = – 5 sau X 2 + 8 X + (A – 40) = 0
O ecuație are două rădăcini dacă D > 0
D = b 2 – 4ac = 64 – 4 (a – 40) = 64 + 1 60 – 4a = 224 – 4a >0,
224– 4a >0;
A< 56
Ecuația f (X ) are trei rădăcini la cea mai mare valoare a = 55
Răspuns: a = 55
și) f (X ) = X 3 + 19 X 2 + topor + b , X 0 = – 6
Din moment ce una dintre rădăcini – 6 , apoi conform schemei lui Horner avem
1
19
A
b
– 6
1
13
a – 78
0
x 3 + 19x 2 + ax + b = (x +6) (x 2 + 13x + (a – 78)) = 0
f (X ) = 0, Dacă x = – 6 sau X 2 + 13 X + (A – 78) = 0
A doua ecuație are două rădăcini dacă
Pentru a utiliza previzualizările prezentării, creați un cont Google și conectați-vă la el: https://accounts.google.com
Subtitrările diapozitivelor:
Ecuații de grade superioare (rădăcinile unui polinom într-o variabilă).
Planul cursului. Numarul 1. Ecuații de grade superioare la cursul de matematică școlară. nr. 2. Forma standard a unui polinom. Nr. 3. Rădăcini întregi ale unui polinom. Schema lui Horner. Nr. 4. Rădăcini fracţionare ale unui polinom. Nr. 5. Ecuații de forma: (x + a)(x + b)(x + c) ... = A Nr. 6. Ecuații reciproce. Nr. 7. Ecuații omogene. Nr. 8. Metoda coeficienților nedeterminați. Nr. 9. Functional - metoda grafica. Nr. 10. Formule Vieta pentru ecuaţii de grade superioare. Nr. 11. Metode nestandardizate de rezolvare a ecuaţiilor de grade superioare.
Ecuații de grade superioare la cursul de matematică școlară. clasa a 7-a. Forma standard a unui polinom. Acțiuni cu polinoame. Factorizarea unui polinom. Într-o clasă obișnuită 42 de ore, într-o clasă specială 56 de ore. 8 clasa speciala. Rădăcini întregi ale unui polinom, împărțirea polinoamelor, ecuații reciproce, diferența și suma puterilor a n-a ale unui binom, metoda coeficienților nedeterminați. Yu.N. Makarychev „Capitole suplimentare la cursul de algebră școlară pentru clasa a 8-a”, M.L. Galitsky Colecția de probleme de algebră pentru clasele 8-9.” 9 clasa speciala. Rădăcini raționale ale unui polinom. Ecuații reciproce generalizate. Formule Vieta pentru ecuații de grade superioare. N.Da. Vilenkin „Algebră clasa a IX-a cu studiu aprofundat. 11 clasa speciala. Identitatea polinoamelor. Polinom în mai multe variabile. Functional - metoda grafica de rezolvare a ecuatiilor de grade superioare.
Forma standard a unui polinom. Polinomul P(x) = a ⁿ x ⁿ + a p-1 x p-1 + … + a₂x ² + a₁x + a₀. Numit polinom de formă standard. a p x ⁿ este termenul conducător al polinomului și p este coeficientul termenului principal al polinomului. Când a n = 1, P(x) se numește polinom redus. iar ₀ este termenul liber al polinomului P(x). n este gradul polinomului.
Rădăcini întregi ale unui polinom. Schema lui Horner. Teorema nr. 1. Dacă un întreg a este rădăcina polinomului P(x), atunci a este un divizor al termenului liber P(x). Exemplul nr. 1. Rezolvați ecuația. X⁴ + 2x³ = 11x² – 4x – 4 Să aducem ecuația la forma standard. X⁴ + 2x³ - 11x² + 4x + 4 = 0. Avem polinomul P(x) = x ⁴ + 2x³ - 11x² + 4x + 4 Divizori ai termenului liber: ± 1, ± 2, ±4. x = 1 rădăcină a ecuației deoarece P(1) = 0, x = 2 este rădăcina ecuației deoarece P(2) = 0 Teorema lui Bezout. Restul împărțirii polinomului P(x) la binomul (x – a) este egal cu P(a). Consecinţă. Dacă a este rădăcina polinomului P(x), atunci P(x) se împarte la (x – a). În ecuația noastră, P(x) este împărțit la (x – 1) și la (x – 2), și deci la (x – 1) (x – 2). La împărțirea P(x) la (x² - 3x + 2), coeficientul dă trinomul x² + 5x + 2 = 0, care are rădăcini x = (-5 ± √17)/2
Rădăcini fracționale ale unui polinom. Teorema nr. 2. Dacă p / g este rădăcina polinomului P(x), atunci p este divizorul termenului liber, g este divizorul coeficientului termenului conducător P(x). Exemplul #2: Rezolvați ecuația. 6x³ - 11x² - 2x + 8 = 0. Divizori ai termenului liber: ±1, ±2, ±4, ±8. Niciunul dintre aceste numere nu satisface ecuația. Nu există rădăcini întregi. Divizori naturali ai coeficientului termenului conducător P(x): 1, 2, 3, 6. Posibile rădăcini fracționale ale ecuației: ±2/3, ±4/3, ±8/3. Prin verificare suntem convinși că P(4/3) = 0. X = 4/3 este rădăcina ecuației. Folosind schema lui Horner, împărțim P(x) la (x – 4/3).
Exemple de soluții independente. Rezolvați ecuațiile: 9x³ - 18x = x – 2, x³ - x² = x – 1, x³ - 3x² -3x + 1 = 0, X⁴ - 2x³ + 2x – 1 = 0, X⁴ - 3x² + 2 = 0 , x ⁵ + 5x³ - 6x² = 0, x ³ + 4x² + 5x + 2 = 0, X⁴ + 4x³ - x ² - 16x – 12 = 0 4x³ + x ² - x + 5 = 0 3x⁴ + 5x³ - 9x² - = 9x + 10 0. Raspunsuri: 1) ±1/3; 2 2) ±1, 3) -1; 2 ±√3, 4) ±1, 5) ± 1; ±√2, 6) 0; 1 7) -2; -1, 8) -3; -1; ±2, 9) – 5/4 10) -2; - 5/3; 1.
Ecuații de forma (x + a)(x + b)(x + c)(x + d)… = A. Exemplul nr. 3. Rezolvați ecuația (x + 1)(x + 2)(x + 3)(x + 4) =24. a = 1, b = 2, c = 3, d = 4 a + d = b + c. Înmulțiți prima paranteză cu a patra și a doua cu a treia. (x + 1)(x + 4)(x + 20(x + 3) = 24. (x² + 5x + 4)(x² + 5x + 6) = 24. Fie x² + 5x + 4 = y , apoi y (y + 2) = 24, y² + 2y – 24 = 0 y₁ = - 6, y₂ = 4. x² + 5x + 4 = -6 sau x² + 5x + 4 = 4. x² + 5x + 10 = 0, D
Exemple de soluții independente. (x + 1)(x + 3)(x + 5)(x + 7) = -15, x (x + 4)(x + 5)(x + 9) + 96 = 0, x (x + 3) )(x + 5)(x + 8) + 56 = 0, (x – 4)(x – 3)(x – 2)(x – 1) = 24, (x – 3)(x -4)( x – 5)(x – 6) = 1680, (x² - 5x)(x + 3)(x – 8) + 108 = 0, (x + 4)² (x + 10)(x – 2) + 243 = 0 (x² + 3x + 2)(x² + 9x + 20) = 4, Notă: x + 3x + 2 = (x + 1)(x + 2), x² + 9x + 20 = (x + 4)( x + 5) Răspunsuri: 1) -4 ±√6; - 6; - 2. 6) - 1; 6; (5± √97)/2 7) -7; -1; -4 ±√3.
Ecuații reciproce. Definiția nr. 1. O ecuație de forma: ax⁴ + inx ³ + cx ² + inx + a = 0 se numește ecuație reciprocă de gradul al patrulea. Definiția nr. 2. O ecuație de forma: ax⁴ + inx ³ + cx ² + kinx + k² a = 0 se numește ecuație reciprocă generalizată de gradul al patrulea. k² a: a = k²; kv: v = k. Exemplul nr. 6. Rezolvați ecuația x ⁴ - 7x³ + 14x² - 7x + 1 = 0. Împărțiți ambele părți ale ecuației la x². x² - 7x + 14 – 7/ x + 1/ x² = 0, (x² + 1/ x²) – 7(x + 1/ x) + 14 = 0. Fie x + 1/ x = y. Punem la patrat ambele laturi ale ecuatiei. x² + 2 + 1/ x² = y², x² + 1/ x² = y² - 2. Obținem ecuația pătratică y² - 7y + 12 = 0, y₁ = 3, y₂ = 4. x + 1/ x =3 sau x + 1/ x = 4. Obținem două ecuații: x² - 3x + 1 = 0, x² - 4x + 1 = 0. Exemplul nr. 7. 3х⁴ - 2х³ - 31х² + 10х + 75 = 0. 75:3 = 25, 10:(– 2) = -5, (-5)² = 25. Condiția ecuației reciproce generalizate este îndeplinită la = -5. Soluția este similară cu exemplul nr. 6. Împărțiți ambele părți ale ecuației la x². 3x⁴ - 2x – 31 + 10/ x + 75/ x² = 0, 3(x⁴ + 25/ x²) – 2(x – 5/ x) – 31 = 0. Fie x – 5/ x = y, le pătratăm pe ambele laturile egalității x² - 10 + 25/ x² = y², x² + 25/ x² = y² + 10. Avem o ecuație pătratică 3y² - 2y – 1 = 0, y₁ = 1, y₂ = - 1/ 3. x – 5/ x = 1 sau x – 5/ x = -1/3. Obținem două ecuații: x² - x – 5 = 0 și 3x² + x – 15 = 0
Exemple de soluții independente. 1. 78x⁴ - 133x³ + 78x² - 133x + 78 = 0. 2. x ⁴ - 5x³ + 10x² - 10x + 4 = 0. 3. x ⁴ - x³ - 10x² + 2x + 4 = 6x³ - 4. 38x² -10x + 24 = 0.5. x ⁴ + 2x³ - 11x² + 4x + 4 = 0. 6. x ⁴ - 5x³ + 10x² -10x + 4 = 0. Răspunsuri: 1) 2/3; 3/2, 2) 1;2 3) -1 ±√3; (3±√17)/2, 4) -1±√3; (7±√337)/12 5) 1; 2; (-5± √17)/2, 6) 1; 2.
Ecuații omogene. Definiție. O ecuație de forma a₀ u³ + a₁ u² v + a₂ uv² + a₃ v³ = 0 se numește ecuație omogenă de gradul trei în raport cu u v. Definiție. O ecuație de forma a₀ u⁴ + a₁ u³v + a₂ u²v² + a₃ uv³ + a₄ v⁴ = 0 se numește ecuație omogenă de gradul al patrulea față de u v. Exemplul nr. 8. Rezolvați ecuația (x² - x + 1)³ + 2x⁴(x² - x + 1) – 3x⁶ = 0 O ecuație omogenă de gradul trei pentru u = x²- x + 1, v = x². Împărțiți ambele părți ale ecuației la x ⁶. Am verificat mai întâi că x = 0 nu este o rădăcină a ecuației. (x² - x + 1/ x²)³ + 2(x² - x + 1/ x²) – 3 = 0. (x² - x + 1)/ x²) = y, y³ + 2y – 3 = 0, y = 1 rădăcina ecuației. Împărțim polinomul P(x) = y³ + 2y – 3 la y – 1 conform schemei lui Horner. În coeficient obținem un trinom care nu are rădăcini. Raspunsul 1.
Exemple de soluții independente. 1. 2(x² + 6x + 1)² + 5(X² + 6X + 1)(X² + 1) + 2(X² + 1)² = 0, 2. (X + 5)⁴ - 13X²(X + 5 )² + 36X⁴ = 0. 3. 2(X² + X + 1)² - 7(X – 1)² = 13(X³ - 1), 4. 2(X -1)⁴ - 5(X² - 3X + 2)² + 2(x – 2)⁴ = 0. 5. (x² + x + 4)² + 3x(x² + x + 4) + 2x² = 0, Răspunsuri: 1) -1; -2±√3, 2) -5/3; -5/4; 5/2; 5 3) -1; -1/2; 2;4 4) ±√2; 3±√2, 5) Nu există rădăcini.
Metoda coeficienților nedeterminați. Teorema nr. 3. Două polinoame P(x) și G(x) sunt identice dacă și numai dacă au același grad și coeficienții acelorași grade ale variabilei în ambele polinoame sunt egali. Exemplul nr. 9. Factorizați polinomul y⁴ - 4y³ + 5y² - 4y + 1. y⁴ - 4y³ + 5y² - 4y + 1 = (y² + уу + с)(y² + в₁у + с₁) =у ⁴ + у³(в₁ + в) с₁ + с + в₁в) + у(с₁ + св₁) + сс ₁. Conform teoremei nr. 3, avem un sistem de ecuații: в₁ + в = -4, с₁ + с + в₁в = 5, сс₁ + св₁ = -4, сс₁ = 1. Este necesar să se rezolve sistemul în numere întregi. Ultima ecuație în numere întregi poate avea soluții: c = 1, c₁ =1; с = -1, с₁ = -1. Fie с = с ₁ = 1, atunci din prima ecuație avem в₁ = -4 –в. Substituim în a doua ecuație a sistemului в² + 4в + 3 = 0, в = -1, в₁ = -3 sau в = -3, в₁ = -1. Aceste valori se potrivesc celei de-a treia ecuații a sistemului. Când с = с ₁ = -1 D
Exemplul nr. 10. Factorizați polinomul y³ - 5y + 2. y³ -5y + 2 = (y + a)(y² + vy + c) = y³ + (a + b)y² + (ab + c)y + ac. Avem un sistem de ecuații: a + b = 0, ab + c = -5, ac = 2. Posibile soluții întregi pentru a treia ecuație: (2; 1), (1; 2), (-2; -1). ), (-1; -2). Fie a = -2, c = -1. Din prima ecuație a sistemului în = 2, care satisface a doua ecuație. Înlocuind aceste valori în egalitatea dorită, obținem răspunsul: (y – 2)(y² + 2y – 1). A doua cale. Y³ - 5y + 2 = y³ -5y + 10 – 8 = (y³ - 8) – 5(y – 2) = (y – 2)(y² + 2y -1).
Exemple de soluții independente. Factorizați polinoamele: 1. y⁴ + 4y³ + 6y² +4y -8, 2. y⁴ - 4y³ + 7y² - 6y + 2, 3. x ⁴ + 324, 4. y⁴ -8y³ + 24y² -32y + 15, 5. Rezolvare ecuația folosind metoda factorizării: a) x ⁴ -3x² + 2 = 0, b) x ⁵ +5x³ -6x² = 0. Răspunsuri: 1) (y² +2y -2)(y² +2y +4), 2) (y – 1)²(y² -2y + 2), 3) (x² -6x + 18)(x² + 6x + 18), 4) (y – 1)(y – 3)(y² - 4у + 5) , 5a) ± 1; ±√2, 5b) 0; 1.
Functional - metoda grafica de rezolvare a ecuatiilor de grade superioare. Exemplul nr. 11. Rezolvați ecuația x ⁵ + 5x -42 = 0. Funcția y = x ⁵ crescător, funcția y = 42 – 5x descrescătoare (k
Exemple de soluții independente. 1. Folosind proprietatea monotonității unei funcții, demonstrați că ecuația are o singură rădăcină și găsiți această rădăcină: a) x ³ = 10 – x, b) x ⁵ + 3x³ - 11√2 – x. Răspunsuri: a) 2, b) √2. 2. Rezolvați ecuația folosind metoda funcțional-grafică: a) x = ³ √x, b) l x l = ⁵ √x, c) 2 = 6 – x, d) (1/3) = x +4, d ) (x – 1)² = log₂ x, e) log = (x + ½)², g) 1 - √x = ln x, h) √x – 2 = 9/x. Răspunsuri: a) 0; ±1, b) 0; 1, c) 2, d) -1, e) 1; 2, f) ½, g) 1, h) 9.
Formule Vieta pentru ecuații de grade superioare. Teorema nr. 5 (teorema lui Vieta). Dacă ecuația a x ⁿ + a x ⁿ + … + a₁x + a₀ are n rădăcini reale diferite x ₁, x ₂, …, x, atunci ele îndeplinesc egalitățile: Pentru o ecuație pătratică ax² + bx + c = o: x ₁ + x₂ = -в/а, x₁х₂ = с/а; Pentru ecuația cubică a₃x ³ + a₂x² + a₁x + a₀ = o: x ₁ + x ₂ + x ₃ = -a₂/a₃; x₁х ₂ + x₁х ₃ + x₂х ₃ = а₁/а₃; x₁х₂х₃ = -а₀/а₃; ..., pentru o ecuație de gradul al n-lea: x ₁ + x ₂ + ... x = - a / a, x₁x ₂ + x₁x ₃ + ... + x x = a / a, ... , x₁x ₂ ·… · x = (- 1 ) ⁿ a₀/a. Teorema inversă este de asemenea valabilă.
Exemplul nr. 13. Scrieți o ecuație cubică ale cărei rădăcini sunt inverse rădăcinilor ecuației x ³ - 6x² + 12x – 18 = 0, iar coeficientul pentru x ³ este 2. 1. Prin teorema lui Vieta pentru ecuația cubică avem: x ₁ + x ₂ + x ₃ = 6, x₁x ₂ + x₁х ₃ + x₂х ₃ = 12, x₁х₂х ₃ = 18. 2. Compunem reciprocele acestor rădăcini și le aplicăm teorema Vieta inversă. 1/ x ₁ + 1/ x ₂ + 1/ x ₃ = (x₂х ₃ + x₁х ₃ + x₁х ₂)/ x₁х₂х ₃ = 12/18 = 2/3. 1/ x₁х ₂ + 1/ x₁х ₃ + 1/ x₂х ₃ = (x ₃ + x ₂ + x ₁)/ x₁х₂х ₃ = 6/18 = 1/3, 1/ x₁х₃/1₃ Obținem ecuația x³ +2/3x² + 1/3x – 1/18 = 0 2 Răspuns: 2x³ + 4/3x² + 2/3x -1/9 = 0.
Exemple de soluții independente. 1. Scrieți o ecuație cubică ale cărei rădăcini sunt pătratele inverse ale rădăcinilor ecuației x ³ - 6x² + 11x – 6 = 0, iar coeficientul lui x ³ este 8. Răspuns: 8x³ - 98/9x² + 28/9x - 2/9 = 0. Metode nestandard de rezolvare a ecuaţiilor de grade superioare. Exemplul nr. 12. Rezolvați ecuația x ⁴ -8x + 63 = 0. Să factorizăm partea stângă a ecuației. Să selectăm pătratele exacte. X⁴ - 8x + 63 = (x⁴ + 16x² + 64) – (16x² + 8x + 1) = (x² + 8)² - (4x + 1)² = (x² + 4x + 9)(x² - 4x + 7) = 0. Ambii discriminatori sunt negativi. Răspuns: fără rădăcini.
Exemplul nr. 14. Rezolvați ecuația 21x³ + x² - 5x – 1 = 0. Dacă termenul inactiv al ecuației este ± 1, atunci ecuația este convertită în ecuația redusă folosind substituția x = 1/y. 21/y³ + 1/y² - 5/y – 1 = 0 · y³, y³ + 5y² -y – 21 = 0. y = -3 rădăcina ecuației. (y + 3)(y² + 2y -7) = 0, y = -1 ± 2√2. x ₁ = -1/3, x ₂ = 1/ -1 + 2√2 = (2√2 + 1)/7, X₃ = 1/-1 -2√2 = (1-2√2)/7 . Exemplul nr. 15. Rezolvați ecuația 4x³-10x² + 14x – 5 = 0. Înmulțiți ambele părți ale ecuației cu 2. 8x³ -20x² + 28x – 10 = 0, (2x)³ - 5(2x)² + 14 (2x) -10 = 0. Să introducem o nouă variabilă y = 2x, obținem ecuația redusă y³ - 5y² + 14y -10 = 0, y = 1 rădăcină a ecuației. (y – 1)(y² - 4y + 10) = 0, D
Exemplul nr. 16. Demonstrați că ecuația x ⁴ + x ³ + x – 2 = 0 are o rădăcină pozitivă. Fie f (x) = x ⁴ + x ³ + x – 2, f’ (x) = 4x³ + 3x² + 1 > o pentru x > o. Funcția f (x) crește pentru x > o, iar valoarea lui f (o) = -2. Este evident că ecuația are o rădăcină pozitivă etc. Exemplul nr. 17. Rezolvați ecuația 8x(2x² - 1)(8x⁴ - 8x² + 1) = 1. I.F. Sharygin „Curs opțional de matematică pentru clasa a 11-a.” M. Iluminismul 1991 p.90. 1. l x l 1 2x² - 1 > 1 și 8x⁴ -8x² + 1 > 1 2. Să facem înlocuirea x = confortabil, y € (0; n). Pentru alte valori ale lui y, valorile lui x se repetă, iar ecuația nu are mai mult de 7 rădăcini. 2х² - 1 = 2 cos²y – 1 = cos2y, 8х⁴ - 8х² + 1 = 2(2х² - 1)² - 1 = 2 cos²2y – 1 = cos4y. 3. Ecuația ia forma 8 cozycos2ycos4y = 1. Înmulțiți ambele părți ale ecuației cu siny. 8 sinycosycos2ycos4y = siny. Aplicând formula unghiului dublu de 3 ori obținem ecuația sin8y = siny, sin8y – siny = 0
Sfârșitul soluției la exemplul nr. 17. Aplicăm formula diferenței sinusurilor. 2 sin7y/2 · cos9y/2 = 0 . Considerând că y € (0;n), y = 2pk/3, k = 1, 2, 3 sau y = n/9 + 2pk/9, k =0, 1, 2, 3. Revenind la variabila x, obținem răspunsul: Cos2 p/7, cos4 p/7, cos6 p/7, cos p/9, ½, cos5 p/9, cos7 p/9. Exemple de soluții independente. Găsiți toate valorile lui a pentru care ecuația (x² + x)(x² + 5x + 6) = a are exact trei rădăcini. Răspuns: 9/16. Instrucțiuni: reprezentați grafic partea stângă a ecuației. F max = f(0) = 9/16 . Linia dreaptă y = 9/16 intersectează graficul funcției în trei puncte. Rezolvați ecuația (x² + 2x)² - (x + 1)² = 55. Răspuns: -4; 2. Rezolvați ecuația (x + 3)⁴ + (x + 5)⁴ = 16. Răspuns: -5; -3. Rezolvați ecuația 2(x² + x + 1)² -7(x – 1)² = 13(x³ - 1).Răspuns: -1; -1/2, 2;4 Aflați numărul de rădăcini reale ale ecuației x ³ - 12x + 10 = 0 pe [-3; 3/2]. Instrucțiuni: găsiți derivatul și investigați monotul.
Exemple de soluții independente (continuare). 6. Aflați numărul de rădăcini reale ale ecuației x ⁴ - 2x³ + 3/2 = 0. Răspuns: 2 7. Fie x ₁, x ₂, x ₃ rădăcinile polinomului P(x) = x ³ - 6x² -15x + 1. Aflați X₁² + x ₂² + x ₃². Răspuns: 66. Direcții: Aplicați teorema lui Vieta. 8. Demonstrați că pentru a > o și o valoare reală arbitrară din ecuația x ³ + ax + b = o are o singură rădăcină reală. Sugestie: Demonstrați prin contradicție. Aplica teorema lui Vieta. 9. Rezolvați ecuația 2(x² + 2)² = 9(x³ + 1). Răspuns: ½; 1; (3 ± √13)/2. Sugestie: aduceți ecuația la o ecuație omogenă folosind egalitățile X² + 2 = x + 1 + x² - x + 1, x³ + 1 = (x + 1)(x² - x + 1). 10. Rezolvați sistemul de ecuații x + y = x², 3y – x = y². Răspuns: (0;0),(2;2), (√2; 2 - √2), (- √2; 2 + √2). 11. Rezolvați sistemul: 4y² -3y = 2x –y, 5x² - 3y² = 4x – 2y. Răspuns: (o;o), (1;1),(297/265; - 27/53).
Test. Opțiunea 1. 1. Rezolvați ecuația (x² + x) – 8(x² + x) + 12 = 0. 2. Rezolvați ecuația (x + 1)(x + 3)(x + 5)(x + 7) = - 15 3. Rezolvați ecuația 12x²(x – 3) + 64(x – 3)² = x ⁴. 4. Rezolvați ecuația x ⁴ - 4x³ + 5x² - 4x + 1 = 0 5. Rezolvați sistemul de ecuații: x ² + 2y² - x + 2y = 6, 1,5x² + 3y² - x + 5y = 12.
Opțiunea 2 1. (x² - 4x)² + 7(x² - 4x) + 12 = 0. 2. x (x + 1)(x + 5)(x + 6) = 24. 3. x ⁴ + 18( x + 4)² = 11x²(x + 4). 4. x ⁴ - 5x³ + 6x² - 5x + 1 = 0. 5. x² - 2xy + y² + 2x²y – 9 = 0, x – y – x²y + 3 = 0. A treia opțiune. 1. (x² + 3x)² - 14(x² + 3x) + 40 = 0 2. (x – 5)(x-3)(x + 3)(x + 1) = - 35. 3. x4 + 8x² (x + 2) = 9(x+ 2)². 4. x ⁴ - 7x³ + 14x² - 7x + 1 = 0. 5. x + y + x² + y² = 18, xy + x² + y² = 19.
Opțiunea 4. (x² - 2x)² - 11(x² - 2x) + 24 = o. (x -7)(x-4)(x-2)(x + 1) = -36. X⁴ + 3(x -6)² = 4x²(6 – x). X⁴ - 6x³ + 7x² - 6x + 1 = 0. X² + 3xy + y² = - 1, 2x² - 3xy – 3y² = - 4. Sarcină suplimentară: Restul împărțirii polinomului P(x) la (x – 1) este 4, restul când este împărțit la (x + 1) este egal cu 2, iar când este împărțit la (x – 2) este egal cu 8. Aflați restul la împărțirea P(x) la (x³ - 2x² - x + 2 ).
Răspunsuri și instrucțiuni: opțiunea Nr. 1 Nr. 2. Nr. 3. Nr. 4. Nr. 5. 1. - 3; ±2; 1 1;2;3. -5; -4; 1; 2. Ecuația omogenă: u = x -3, v = x² -2 ; -1; 3; 4. (2;1); (2/3;4/3). Sugestie: 1·(-3) + 2· 2 2. -6; -2; -4±√6. -3±2√3; - 4; - 2. 1±√11; 4; - 2. Ecuație omogenă: u = x + 4, v = x² 1; 5;3±√13. (2;1); (0;3); (- treizeci). Sugestie: 2 2 + 1. 3. -6; 2; 4; 12 -3; -2; 4; 12 -6; -3; -1; 2. Omogen u = x+ 2, v = x² -6; ±3; 2 (2;3), (3;2), (-2 + √7; -2 - √7); (-2 - √7; -2 + √7). Instruire: 2 -1. 4. (3±√5)/2 2±√3 2±√3; (3±√5)/2 (5 ± √21)/2 (1;-2), (-1;2). Sugestie: 1·4 + 2 .
Rezolvarea unei sarcini suplimentare. După teorema lui Bezout: P(1) = 4, P(-1) = 2, P(2) = 8. P(x) = G(x) (x³ - 2x² - x + 2) + ax² + inx + Cu . Inlocuitor 1; - 1; 2. P(1) = G(1) 0 + a + b + c = 4, a + b+ c = 4. P(-1) = a – b + c = 2, P(2) = 4a² + 2b + c = 8. Rezolvând sistemul rezultat de trei ecuații, obținem: a = b = 1, c = 2. Răspuns: x² + x + 2.
Criteriul nr. 1 - 2 puncte. 1 punct – o eroare de calcul. Nr. 2,3,4 – 3 puncte fiecare. 1 punct – a condus la o ecuație pătratică. 2 puncte – o eroare de calcul. Nr 5. – 4 puncte. 1 punct – exprimă o variabilă în termenii alteia. 2 puncte – a primit una dintre soluții. 3 puncte – o eroare de calcul. Sarcină suplimentară: 4 puncte. 1 punct – a aplicat teorema lui Bezout pentru toate cele patru cazuri. 2 puncte – a compilat un sistem de ecuații. 3 puncte – o eroare de calcul.
În general, o ecuație de grad mai mare de 4 nu poate fi rezolvată în radicali. Dar uneori mai putem găsi rădăcinile unui polinom din stânga într-o ecuație de cel mai înalt grad dacă o reprezentăm ca produs de polinoame la un grad de cel mult 4. Rezolvarea unor astfel de ecuații se bazează pe factorizarea unui polinom, așa că vă sfătuim să revizuiți acest subiect înainte de a studia acest articol.
Cel mai adesea ai de-a face cu ecuații de grade superioare cu coeficienți întregi. În aceste cazuri, putem încerca să găsim rădăcini raționale și apoi factorizați polinomul astfel încât apoi să îl putem transforma într-o ecuație de grad inferior care este ușor de rezolvat. În acest material ne vom uita la astfel de exemple.
Ecuații de grad superior cu coeficienți întregi
Toate ecuațiile de forma a n x n + a n - 1 x n - 1 + . . . + a 1 x + a 0 = 0 , putem produce o ecuație de același grad înmulțind ambele părți cu a n n - 1 și făcând o modificare variabilă de forma y = a n x:
un n x n + un n - 1 x n - 1 + . . . + a 1 x + a 0 = 0 a n n · x n + a n - 1 · a n n - 1 · x n - 1 + … + a 1 · (a n) n - 1 · x + a 0 · (a n) n - 1 = 0 y = a n x ⇒ y n + b n - 1 y n - 1 + … + b 1 y + b 0 = 0
Coeficienții rezultați vor fi, de asemenea, întregi. Astfel, va trebui să rezolvăm ecuația redusă de gradul al n-lea cu coeficienți întregi, având forma x n + a n x n - 1 + ... + a 1 x + a 0 = 0.
Calculăm rădăcinile întregi ale ecuației. Dacă ecuația are rădăcini întregi, trebuie să le căutați printre divizorii termenului liber a 0 . Să le notăm și să le substituim în egalitatea originală unul câte unul, verificând rezultatul. Odată ce am obținut identitatea și am găsit una dintre rădăcinile ecuației, o putem scrie sub forma x - x 1 · P n - 1 (x) = 0. Aici x 1 este rădăcina ecuației, iar P n - 1 (x) este câtul x n + a n x n - 1 + ... + a 1 x + a 0 împărțit la x - x 1 .
Înlocuim divizorii rămași scriși în P n - 1 (x) = 0, începând cu x 1, deoarece rădăcinile pot fi repetate. După obținerea identității, rădăcina x 2 se consideră găsită, iar ecuația poate fi scrisă sub forma (x - x 1) (x - x 2) · P n - 2 (x) = 0. Aici P n - 2 (x) va fi câtul împărțirii P n - 1 (x) la x - x 2.
Continuăm să sortăm prin divizori. Să găsim toate rădăcinile întregi și să le notăm numărul ca m. După aceasta, ecuația inițială poate fi reprezentată ca x - x 1 x - x 2 · … · x - x m · P n - m (x) = 0. Aici P n - m (x) este un polinom de n - m grad. Pentru calcul este convenabil să folosiți schema lui Horner.
Dacă ecuația noastră originală are coeficienți întregi, nu putem obține în cele din urmă rădăcini fracționale.
Am ajuns la ecuația P n - m (x) = 0, ale cărei rădăcini pot fi găsite în orice mod convenabil. Ele pot fi iraționale sau complexe.
Să arătăm cu un exemplu specific cum este utilizată această schemă de soluții.
Exemplul 1
Condiție: găsiți soluția ecuației x 4 + x 3 + 2 x 2 - x - 3 = 0.
Soluţie
Să începem prin a găsi rădăcini întregi.
Avem un termen liber egal cu minus trei. Are divizori egali cu 1, - 1, 3 și - 3. Să le substituim în ecuația originală și să vedem care dintre ele dă identitățile rezultate.
Cu x egal cu unu, obținem 1 4 + 1 3 + 2 · 1 2 - 1 - 3 = 0, ceea ce înseamnă că unul va fi rădăcina acestei ecuații.
Acum să împărțim polinomul x 4 + x 3 + 2 x 2 - x - 3 la (x - 1) într-o coloană:
Deci x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.
1 3 + 2 1 2 + 4 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 (- 1) 2 + 4 - 1 + 3 = 0
Am obținut o identitate, ceea ce înseamnă că am găsit o altă rădăcină a ecuației, egală cu - 1.
Împărțiți polinomul x 3 + 2 x 2 + 4 x + 3 la (x + 1) într-o coloană:
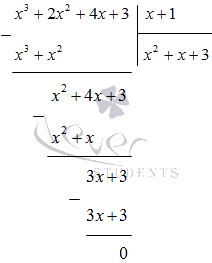
Înțelegem asta
x 4 + x 3 + 2 x 2 - x - 3 = (x - 1) (x 3 + 2 x 2 + 4 x + 3) = = (x - 1) (x + 1) (x 2 + x + 3)
Inlocuim urmatorul divizor in egalitatea x 2 + x + 3 = 0, incepand de la - 1:
1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0
Egalitățile rezultate vor fi incorecte, ceea ce înseamnă că ecuația nu mai are rădăcini întregi.
Rădăcinile rămase vor fi rădăcinile expresiei x 2 + x + 3.
D = 1 2 - 4 1 3 = - 11< 0
De aici rezultă că acest trinom pătratic nu are rădăcini reale, dar există și conjugate complexe: x = - 1 2 ± i 11 2.
Să clarificăm că în loc să ne împărțim într-o coloană, poate fi folosită schema lui Horner. Acest lucru se face astfel: după ce am determinat prima rădăcină a ecuației, completăm tabelul.
În tabelul de coeficienți putem vedea imediat coeficienții coeficientului împărțirii polinoamelor, ceea ce înseamnă x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3 .
După ce găsim următoarea rădăcină, care este - 1, obținem următoarele:
Răspuns: x = - 1, x = 1, x = - 1 2 ± i 11 2.
Exemplul 2
Condiție: rezolvați ecuația x 4 - x 3 - 5 x 2 + 12 = 0.
Soluţie
Termenul liber are divizori 1, - 1, 2, - 2, 3, - 3, 4, - 4, 6, - 6, 12, - 12.
Să le verificăm în ordine:
1 4 - 1 3 - 5 1 2 + 12 = 7 ≠ 0 (- 1) 4 - (- 1) 3 - 5 (- 1) 2 + 12 = 9 ≠ 0 2 4 2 3 - 5 2 2 + 12 = 0
Aceasta înseamnă că x = 2 va fi rădăcina ecuației. Împărțiți x 4 - x 3 - 5 x 2 + 12 la x - 2 folosind schema lui Horner:
Ca rezultat, obținem x - 2 (x 3 + x 2 - 3 x - 6) = 0.
2 3 + 2 2 - 3 2 - 6 = 0
Aceasta înseamnă că 2 va fi din nou rădăcina. Împărțiți x 3 + x 2 - 3 x - 6 = 0 la x - 2:
Ca rezultat, obținem (x - 2) 2 · (x 2 + 3 x + 3) = 0.
Verificarea divizorilor rămași nu are sens, deoarece egalitatea x 2 + 3 x + 3 = 0 este mai rapidă și mai convenabilă de rezolvat folosind discriminantul.
Să rezolvăm ecuația pătratică:
x 2 + 3 x + 3 = 0 D = 3 2 - 4 1 3 = - 3< 0
Obținem o pereche complexă de rădăcini conjugate: x = - 3 2 ± i 3 2 .
Răspuns: x = - 3 2 ± i 3 2 .
Exemplul 3
Condiție: Aflați rădăcinile reale pentru ecuația x 4 + 1 2 x 3 - 5 2 x - 3 = 0.
Soluţie
x 4 + 1 2 x 3 - 5 2 x - 3 = 0 2 x 4 + x 3 - 5 x - 6 = 0
Înmulțim 2 3 de ambele părți ale ecuației:
2 x 4 + x 3 - 5 x - 6 = 0 2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0
Înlocuiți variabilele y = 2 x:
2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0 y 4 + y 3 - 20 y - 48 = 0
Ca urmare, am obținut o ecuație standard de gradul 4, care poate fi rezolvată conform schemei standard. Să verificăm divizorii, să împărțim și în cele din urmă să obținem că are 2 rădăcini reale y = - 2, y = 3 și două complexe. Nu vom prezenta aici întreaga soluție. Datorită substituției, rădăcinile reale ale acestei ecuații vor fi x = y 2 = - 2 2 = - 1 și x = y 2 = 3 2.
Răspuns: x 1 = - 1 , x 2 = 3 2
Dacă observați o eroare în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter
Textul lucrării este postat fără imagini și formule.
Versiunea completă a lucrării este disponibilă în fila „Fișiere de lucru” în format PDF
Introducere
Rezolvarea ecuațiilor algebrice de grade superioare cu o necunoscută este una dintre cele mai dificile și mai vechi probleme matematice. Cei mai remarcabili matematicieni ai antichității s-au ocupat de aceste probleme.
Rezolvarea ecuațiilor de gradul al n-lea este o sarcină importantă pentru matematica modernă. Există destul de mult interes pentru ele, deoarece aceste ecuații sunt strâns legate de căutarea rădăcinilor ecuațiilor care nu sunt acoperite în programa școlară de matematică.
Problemă: Lipsa studenților de abilități în rezolvarea ecuațiilor de grade superioare în diferite moduri îi împiedică să se pregătească cu succes pentru certificarea finală în matematică și olimpiade de matematică și să se antreneze într-o clasă specializată de matematică.
Faptele enumerate au determinat relevanţă lucrarea noastră „Rezolvarea ecuațiilor de grade superioare”.
Cunoașterea celor mai simple metode de rezolvare a ecuațiilor de gradul al n-lea reduce timpul de realizare a unei sarcini, de care depind rezultatul muncii și calitatea procesului de învățare.
Scopul lucrării: studierea metodelor cunoscute de rezolvare a ecuațiilor de grade superioare și identificarea celor mai accesibile dintre ele pentru utilizare practică.
Pe baza scopului, în lucrare sunt definite următoarele: sarcini:
Studiați literatura și resursele de pe Internet pe această temă;
Familiarizați-vă cu fapte istorice legate de acest subiect;
Descrieți diferite moduri de rezolvare a ecuațiilor de grad superior
comparați gradul de complexitate al fiecăruia dintre ele;
Introduceți colegii de clasă modalități de rezolvare a ecuațiilor de grade superioare;
Creați o selecție de ecuații pentru aplicarea practică a fiecăreia dintre metodele luate în considerare.
Obiect de studiu- ecuaţii de grade superioare cu o variabilă.
Subiect de studiu- metode de rezolvare a ecuaţiilor de grade superioare.
Ipoteză: Nu există o metodă generală sau un algoritm unic care să permită găsirea soluțiilor ecuațiilor de gradul al n-lea într-un număr finit de pași.
Metode de cercetare:
- metoda bibliografică (analiza literaturii pe tema de cercetare);
- metoda de clasificare;
- metoda analizei calitative.
Semnificație teoretică cercetarea constă în sistematizarea metodelor de rezolvare a ecuaţiilor de grade superioare şi descrierea algoritmilor acestora.
Semnificație practică- a prezentat material pe această temă și elaborarea unui suport didactic pentru studenți pe această temă.
1. ECUAȚII DE GRADE SUPERIOARE
1.1 Conceptul de ecuație de gradul al n-lea
Definiția 1. O ecuație de gradul al n-lea este o ecuație de formă
A 0 xⁿ+a 1 X n -1 +a 2 xⁿ - ²+…+a n -1 x+a n = 0, unde coeficienți A 0, A 1, A 2…, A n -1, A n- orice numere reale și ,A 0 ≠ 0 .
Polinom A 0 xⁿ+a 1 X n -1 +a 2 xⁿ - ²+…+a n -1 x+a n se numește polinom de gradul al n-lea. Coeficienții se disting prin nume: A 0 - coeficient senior; A n este membru liber.
Definiție 2. Soluții sau rădăcini pentru o ecuație dată sunt toate valorile variabilei X, care transformă această ecuație într-o egalitate numerică adevărată sau, pentru care polinomul A 0 xⁿ+a 1 X n -1 +a 2 xⁿ - ²+…+a n -1 x+a n merge la zero. Această valoare variabilă X numită și rădăcina unui polinom. Rezolvarea unei ecuații înseamnă găsirea tuturor rădăcinilor acesteia sau stabilirea faptului că nu există.
Dacă A 0 = 1, atunci o astfel de ecuație se numește ecuație rațională cu număr întreg redus n th grade.
Pentru ecuațiile de gradul al treilea și al patrulea, există formule Cardano și Ferrari care exprimă rădăcinile acestor ecuații prin radicali. S-a dovedit că în practică sunt rar folosite. Astfel, dacă n ≥ 3, iar coeficienții polinomului sunt numere reale arbitrare, atunci găsirea rădăcinilor ecuației nu este o sarcină ușoară. Cu toate acestea, în multe cazuri speciale, această problemă este complet rezolvată. Să ne uităm la unele dintre ele.
1.2 Fapte istorice pentru rezolvarea ecuațiilor de grad superior
Deja în antichitate, oamenii și-au dat seama cât de important era să înveți să rezolvi ecuațiile algebrice. Cu aproximativ 4000 de ani în urmă, oamenii de știință babilonieni știau cum să rezolve o ecuație pătratică și să rezolve sisteme de două ecuații, dintre care una era de gradul doi. Cu ajutorul ecuațiilor de grade superioare, au fost rezolvate diverse probleme de topografie, arhitectură și afaceri militare; la ele s-au redus multe și variate întrebări de practică și științe naturale, deoarece limbajul precis al matematicii permite pur și simplu exprimarea faptelor și a relațiilor. , care, atunci când este enunțat într-un limbaj obișnuit, poate părea confuz și complex.
O formulă universală pentru găsirea rădăcinilor unei ecuații algebrice al n-lea nici-o calificare. Mulți, desigur, au avut ideea tentantă de a găsi, pentru orice grad n, formule care să exprime rădăcinile ecuației prin coeficienții ei, adică să rezolve ecuația în radicali.
Abia în secolul al XVI-lea, matematicienii italieni au reușit să avanseze mai departe - să găsească formule pentru n = 3 și n = 4. În același timp, Scipio, Dahl, Ferro și studenții săi Fiori și Tartaglia studiau problema soluției generale a ecuații de gradul 3.
În 1545, a fost publicată cartea matematicianului italian D. Cardano „Marea artă, sau despre regulile algebrei”, unde, alături de alte întrebări de algebră, sunt luate în considerare metode generale de rezolvare a ecuațiilor cubice, precum și o metodă pentru rezolvarea ecuațiilor de gradul IV, descoperite de elevul său L. Ferrari.
O prezentare completă a problemelor legate de rezolvarea ecuațiilor de gradul III și IV a fost făcută de F. Viet.
În anii 20 ai secolului al XIX-lea, matematicianul norvegian N. Abel a demonstrat că rădăcinile ecuațiilor de gradul al cincilea nu pot fi exprimate în termeni de radicali.
Studiul a arătat că știința modernă cunoaște multe modalități de a rezolva ecuațiile de gradul al n-lea.
Rezultatul căutării metodelor de rezolvare a ecuațiilor de grade superioare care nu pot fi rezolvate cu ajutorul metodelor avute în vedere în programa școlară au fost metode bazate pe aplicarea teoremei lui Vieta (pentru ecuațiile de grad n>2), teoremele lui Bezout, schemele lui Horner, precum și formula Cardano și Ferrari pentru rezolvarea ecuațiilor cubice și quartice.
Lucrarea prezintă metode de rezolvare a ecuațiilor și tipurile acestora, care au devenit o descoperire pentru noi. Acestea includ metoda coeficienților nedeterminați, selectarea gradului complet, ecuații simetrice.
2. SOLUȚIONAREA INTEGRAȚIILOR ECUATII DE GRADE SUPERIOARE CU COEFICIENȚI INTEGRI
2.1 Rezolvarea ecuațiilor de gradul 3. Formula D. Cardano
Luați în considerare ecuații de formă X 3 +px+q=0. Să transformăm ecuația generală în forma: X 3 +px 2 +qx+r=0. Să notăm formula pentru cubul sumei; Să o adăugăm la egalitatea originală și să o înlocuim cu y. Obtinem ecuatia: y 3 + (q -) (y -) + (r - =0. După transformări, avem: y 2 +py + q=0. Acum, să scriem din nou formula cubului sumei:
(a+b) 3 =a 3 + 3a 2 b + 3ab 2 + b 3 = a 3 + b 3 + 3ab (a + b), a inlocui ( a+b)pe X, obținem ecuația X 3 - 3abx - (a 3 +b 3) = 0. Acum putem vedea că ecuația inițială este echivalentă cu sistemul: și Rezolvând sistemul, obținem:
Am obținut o formulă pentru rezolvarea ecuației de gradul 3 de mai sus. Poartă numele matematicianului italian Cardano.
Să ne uităm la un exemplu. Rezolvați ecuația: .
Avem R= 15 și q= 124, apoi folosind formula Cardano calculăm rădăcina ecuației
Concluzie: această formulă este bună, dar nu este potrivită pentru rezolvarea tuturor ecuațiilor cubice. În același timp, este greoaie. Prin urmare, în practică este rar folosit.
Dar oricine stăpânește această formulă o poate folosi atunci când rezolvă ecuații de gradul trei la examenul de stat unificat.
2.2 Teorema lui Vieta
Dintr-un curs de matematică știm această teoremă pentru o ecuație pătratică, dar puțini oameni știu că este folosită și pentru a rezolva ecuații de ordin superior.
Luați în considerare ecuația:
Să factorizăm partea stângă a ecuației și să împărțim la ≠ 0.
Să transformăm partea dreaptă a ecuației în formă
; De aici rezultă că putem scrie următoarele egalități în sistem:
Formulele derivate de Viète pentru ecuațiile pătratice și demonstrate de noi pentru ecuațiile de gradul 3 sunt valabile și pentru polinoamele de grade superioare.
Să rezolvăm ecuația cubică:
Concluzie: această metodă este universală și suficient de ușor de înțeles pentru elevi, deoarece teorema lui Vieta le este familiară din programa școlară pentru n. = 2. În același timp, pentru a găsi rădăcinile ecuațiilor folosind această teoremă, trebuie să aveți bune abilități de calcul.
2.3 Teorema lui Bezout
Această teoremă poartă numele matematicianului francez din secolul al XVIII-lea J. Bezou.
Teorema. Dacă ecuaţia A 0 xⁿ+a 1 X n -1 +a 2 xⁿ - ²+…+a n -1 x+a n = 0, în care toți coeficienții sunt numere întregi, iar termenul liber este diferit de zero și are o rădăcină întreagă, atunci această rădăcină este un divizor al termenului liber.
Având în vedere că în partea stângă a ecuației există un polinom de gradul al n-lea, teorema are o altă interpretare.
Teorema. La împărțirea unui polinom de gradul al n-lea față de X prin binom x-a restul este egal cu valoarea dividendului când x = a. (scrisoare A poate desemna orice număr real sau imaginar, adică orice număr complex).
Dovada: lăsa f(x) denotă un polinom arbitrar de gradul al n-lea față de variabila x și fie, atunci când este împărțit la un binom ( x-a) s-a dovedit în privat q(x), iar restul R. Este evident că q(x) va exista un polinom (n - 1) gradul relativ la X, iar restul R va fi o valoare constantă, adică independent de X.
Dacă restul R a fost un polinom de gradul I în raport cu x, atunci aceasta ar însemna că împărțirea a eșuat. Asa de, R din X nu depinde. Prin definiția diviziunii obținem identitatea: f(x)=(x-a) q(x)+R.
Egalitatea este adevărată pentru orice valoare a lui x, ceea ce înseamnă că este adevărată și pentru x=a, primim: f(a)=(a-a) q(a)+R. Simbol fa) denotă valoarea polinomului f (X) la x=a, q(a) reprezintă valoare q(x) la x=a. Rest R a rămas la fel ca înainte, pentru că R din X nu depinde. Muncă ( x-a) q(a) = 0, deoarece factorul ( x-a) = 0,și multiplicatorul q(a) există un anumit număr. Prin urmare, din egalitate obținem: f(a)= R, etc.
Exemplul 1. Aflați restul unui polinom X 3 - 3X 2 + 6X- 5 pe binom
X- 2. Prin teorema lui Bezout : R=f(2) = 23-322 + 62 -5=3. Răspuns: R= 3.
Rețineți că teorema lui Bezout este importantă nu atât în sine, cât pentru consecințele sale. (Anexa 1)
Să ne oprim asupra analizei unor tehnici de aplicare a teoremei lui Bezout la rezolvarea problemelor practice. Trebuie remarcat faptul că atunci când rezolvăm ecuații folosind teorema lui Bezout, este necesar:
Găsiți toți divizorii întregi ai termenului liber;
Găsiți cel puțin o rădăcină a ecuației din acești divizori;
Împărțiți partea stângă a ecuației cu (Ha);
Notați produsul divizorului și câtul în partea stângă a ecuației;
Rezolvați ecuația rezultată.
Să ne uităm la exemplul de rezolvare a ecuației x 3 + 4X 2 + x - 6 = 0 .
Rezolvare: găsiți divizorii termenului liber ±1 ; ± 2; ± 3; ± 6. Să calculăm valorile la x= 1, 1 3 + 41 2 + 1- 6=0. Împărțiți partea stângă a ecuației la ( X- 1). Să facem împărțirea folosind un „colț” și obținem:
Concluzie: Teorema lui Bezout este una dintre metodele pe care le avem în vedere în lucrarea noastră, studiată în programul de cursuri opționale. Este greu de înțeles, deoarece pentru a-l stăpâni, trebuie să cunoști toate consecințele din ea, dar, în același timp, teorema lui Bezout este unul dintre asistenții principali pentru studenții la examenul de stat unificat.
2.4 Schema Horner
A împărți un polinom la un binom x-α poți folosi o tehnică simplă specială inventată de matematicienii englezi din secolul al XVII-lea, numită mai târziu schema lui Horner. Pe lângă găsirea rădăcinilor ecuațiilor, folosind schema lui Horner, puteți calcula mai simplu valorile acestora. Pentru a face acest lucru, trebuie să înlocuiți valoarea variabilei în polinomul Pn (x)=a 0 xn+a 1 X n-1 +a 2 xⁿ - ²+…++a n -1 x+a n. (1)
Luați în considerare împărțirea polinomului (1) la binom X-α.
Să exprimăm coeficienții coeficientului incomplet b 0 xⁿ - ¹+ b 1 xⁿ - ²+ b 2 xⁿ - ³+…+ bn -1 iar restul r prin coeficienții polinomului Pn( X) și numărul α. b 0 =a 0 , b 1 = α b 0 +a 1 , b 2 = α b 1 +a 2 …, bn -1 =
= α bn -2 +a n -1 = α bn -1 +a n .
Calculele folosind schema lui Horner sunt prezentate în următorul tabel:
|
A 0 |
A 1 |
A 2 , |
|||
|
b 0 =a 0 |
b 1 = α b 0 +a 1 |
b 2 = α b 1 +a 2 |
r=α b n-1 +a n |
Deoarece r=Pn(α), atunci α este rădăcina ecuației. Pentru a verifica dacă α este o rădăcină multiplă, schema lui Horner poate fi aplicată coeficientului b 0 x+ b 1 x+…+ bn -1 conform tabelului. Dacă în coloana de sub bn -1 rezultatul este din nou 0, ceea ce înseamnă că α este o rădăcină multiplă.
Să ne uităm la un exemplu: rezolvă ecuația X 3 + 4X 2 + x - 6 = 0.
Să aplicăm în partea stângă a ecuației factorizarea polinomului din partea stângă a ecuației, schema lui Horner.
Rezolvare: găsiți divizorii termenului liber ± 1; ± 2; ± 3; ± 6.
|
6 ∙ 1 + (-6) = 0 |
Coeficienții coeficientului sunt numerele 1, 5, 6, iar restul r = 0.
Mijloace, X 3 + 4X 2 + X - 6 = (X - 1) (X 2 + 5X + 6) = 0.
De aici: X- 1 = 0 sau X 2 + 5X + 6 = 0.
X = 1, X 1 = -2; X 2 = -3. Răspuns: 1,- 2, - 3.
Concluzie: Astfel, pe o ecuație am arătat utilizarea a două metode diferite de factorizare a polinoamelor. În opinia noastră, schema lui Horner este cea mai practică și mai economică.
2.5 Rezolvarea ecuațiilor de gradul 4. metoda Ferrari
Studentul lui Cardano, Ludovic Ferrari, a descoperit o modalitate de a rezolva o ecuație de gradul al patrulea. Metoda Ferrari constă din două etape.
Etapa I: ecuațiile de formă sunt reprezentate ca produsul a două trinoame pătrate; aceasta rezultă din faptul că ecuația este de gradul 3 și are cel puțin o soluție.
Etapa II: ecuațiile rezultate sunt rezolvate folosind factorizarea, dar pentru a găsi factorizarea necesară, trebuie rezolvate ecuațiile cubice.
Ideea este de a reprezenta ecuațiile sub forma A 2 =B 2, unde A= X 2 +s,
Funcția B-liniară a X. Apoi rămâne de rezolvat ecuațiile A = ±B.
Pentru claritate, luați în considerare ecuația: Izolând gradul 4, obținem: Pentru oricare d expresia va fi un pătrat perfect. Adăugați ambele părți ale ecuației pe care o obținem
În partea stângă există un pătrat complet, pe care îl puteți ridica d, astfel încât și partea dreaptă a lui (2) devine un pătrat complet. Să ne imaginăm că am reușit acest lucru. Atunci ecuația noastră arată astfel:
Găsirea rădăcinii nu va fi dificilă mai târziu. Pentru a alege corect d este necesar ca discriminantul laturii drepte a lui (3) să devină zero, i.e.
Deci pentru a găsi d, trebuie să rezolvăm această ecuație de gradul 3. Această ecuație auxiliară se numește rezolutiv.
Găsim cu ușurință întreaga rădăcină a soluției: d = 1
Înlocuind ecuația în (1) obținem
Concluzie: metoda Ferrari este universală, dar complexă și greoaie. În același timp, dacă algoritmul de soluție este clar, atunci ecuațiile de gradul 4 pot fi rezolvate folosind această metodă.
2.6 Metoda coeficienților incerti
Succesul rezolvării unei ecuații de gradul 4 folosind metoda Ferrari depinde dacă rezolvăm soluția - o ecuație de gradul 3, care, după cum știm, nu este întotdeauna posibilă.
Esența metodei coeficienților nedeterminați este că se ghicește tipul de factori în care se descompune un anumit polinom, iar coeficienții acestor factori (și polinoame) sunt determinați prin înmulțirea factorilor și echivalarea coeficienților la aceleași puteri ale variabil.
Exemplu: rezolvați ecuația:
Să presupunem că partea stângă a ecuației noastre poate fi descompusă în două trinoame pătrate cu coeficienți întregi astfel încât egalitatea identică să fie adevărată
Evident, coeficienții din fața lor trebuie să fie egali cu 1, iar termenii liberi trebuie să fie egali cu unu + 1, celălalt - 1.
Coeficienții care se confruntă cu X. Să le notăm prin Ași pentru a le determina, înmulțim ambele trinoame din partea dreaptă a ecuației.
Ca rezultat obținem:
Echivalarea coeficienților la aceleași grade X pe părțile din stânga și din dreapta ale egalității (1), obținem un sistem pentru găsirea și
După ce am rezolvat acest sistem, vom avea
Deci ecuația noastră este echivalentă cu ecuația
După ce am rezolvat-o, obținem următoarele rădăcini: .
Metoda coeficienților nedeterminați se bazează pe următoarele afirmații: orice polinom de gradul al patrulea din ecuație poate fi descompus în produsul a două polinoame de gradul doi; două polinoame sunt identic egale dacă și numai dacă coeficienții lor sunt egali pentru aceleași puteri X.
2.7 Ecuații simetrice
Definiție. O ecuație de formă se numește simetrică dacă primii coeficienți din stânga ecuației sunt egali cu primii coeficienți din dreapta.
Vedem că primii coeficienți din stânga sunt egali cu primii coeficienți din dreapta.
Dacă o astfel de ecuație are un grad impar, atunci are o rădăcină X= - 1. În continuare putem scădea gradul ecuației împărțind-o la ( x+ 1). Se pare că atunci când împărțim o ecuație simetrică la ( x+ 1) se obține o ecuație simetrică de grad par. Dovada simetriei coeficienților este prezentată mai jos. (Anexa 6) Sarcina noastră este să învățăm cum să rezolvăm ecuații simetrice de grad par.
De exemplu: (1)
Să rezolvăm ecuația (1), împărțim la X 2 (la grad mediu) = 0.
Să grupăm termenii cu simetric
) + 3(X+ . Să notăm la= X+ , să pătram ambele laturi, deci = la 2 Deci, 2( la 2 sau 2 la 2 + 3 rezolvând ecuația, obținem la = , la= 3. În continuare, să revenim la înlocuire X+ = și X+ = 3. Obținem ecuațiile și Prima nu are soluție, iar a doua are două rădăcini. Răspuns:.
Concluzie: acest tip de ecuație nu se întâlnește des, dar dacă dai peste el, atunci poate fi rezolvată ușor și simplu, fără a apela la calcule greoaie.
2.8 Izolarea unui grad complet
Luați în considerare ecuația.
Partea stângă este cubul sumei (x+1), adică.
Extragem a treia rădăcină din ambele părți: , apoi obținem
Unde este singura rădăcină?
REZULTATE CERCETĂRI
Pe baza rezultatelor lucrării, am ajuns la următoarele concluzii:
Datorită teoriei studiate, ne-am familiarizat cu diverse metode de rezolvare a ecuațiilor întregi de grade superioare;
Formula lui D. Cardano este dificil de utilizat și oferă o probabilitate mare de a face erori în calcul;
− Metoda lui L. Ferrari permite reducerea soluției la o ecuație de gradul al patrulea la una cubică;
− Teorema lui Bezout poate fi folosită atât pentru ecuațiile cubice, cât și pentru ecuațiile de gradul al patrulea; este mai ușor de înțeles și mai vizual atunci când este aplicat la rezolvarea ecuațiilor;
Schema lui Horner ajută la reducerea și simplificarea semnificativă a calculelor în rezolvarea ecuațiilor. Pe lângă găsirea rădăcinilor, folosind schema lui Horner puteți calcula mai simplu valorile polinoamelor din partea stângă a ecuației;
De interes deosebit au fost soluțiile ecuațiilor prin metoda coeficienților nedeterminați și soluția ecuațiilor simetrice.
În cadrul lucrărilor de cercetare s-a constatat că elevii se familiarizează cu cele mai simple metode de rezolvare a ecuațiilor de cel mai înalt grad la orele opționale de matematică, începând din clasa a IX-a sau a X-a, precum și la cursurile speciale de la școlile de matematică în vizită. Acest fapt a fost stabilit în urma unui sondaj între profesori de matematică de la MBOU „Școala Gimnazială Nr. 9” și elevi care au manifestat un interes sporit pentru disciplina „matematică”.
Cele mai populare metode de rezolvare a ecuațiilor de grade superioare, care se întâlnesc la rezolvarea olimpiadelor, a problemelor competitive și ca urmare a pregătirii studenților pentru examene, sunt metode bazate pe aplicarea teoremei lui Bezout, a schemei lui Horner și a introducerii unei noi variabile.
Demonstrarea rezultatelor muncii de cercetare, de ex. metodele de rezolvare a ecuațiilor nepredate în programa școlară de matematică i-au interesat pe colegii mei.
Concluzie
După ce a studiat literatura educațională și științifică, resursele de pe Internet în forumuri educaționale pentru tineret




