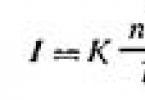1 faktas.
\(\bullet\) Paimkite kai kuriuos ne neigiamas skaičius\(a\) (t. y. \(a\geqslant 0\) ). Tada (aritmetika) kvadratinė šaknis iš skaičiaus \(a\) vadinamas toks neneigiamas skaičius \(b\), sudėjus jį kvadratu gauname skaičių \(a\) : \[\sqrt a=b\quad \text(tas pats kaip )\quad a=b^2\] Iš apibrėžimo išplaukia, kad \(a\geqslant 0, b\geqslant 0\). Šie apribojimai yra svarbi egzistavimo sąlyga kvadratinė šaknis Ir juos reikia prisiminti!
Prisiminkite, kad bet koks skaičius kvadratu duoda neneigiamą rezultatą. Tai yra, \(100^2=10000\geqslant 0\) ir \((-100)^2=10000\geqslant 0\) .
\(\bullet\) Kas yra \(\sqrt(25)\)? Žinome, kad \(5^2=25\) ir \((-5)^2=25\) . Kadangi pagal apibrėžimą turime rasti neneigiamą skaičių, \(-5\) netinka, taigi \(\sqrt(25)=5\) (nes \(25=5^2\) ).
Reikšmės \(\sqrt a\) radimas vadinamas kvadratine šaknimis iš skaičiaus \(a\), o skaičius \(a\) vadinamas šaknies išraiška.
\(\bullet\) Remiantis apibrėžimu, išraiškos \(\sqrt(-25)\) , \(\sqrt(-4)\) ir kt. neturi prasmės.

2 faktas.
Norint greitai atlikti skaičiavimus, bus naudinga išmokti kvadratų lentelę natūraliuosius skaičius nuo \(1\) iki \(20\): \[\begin(masyvas)(|ll|) \hline 1^2=1 & \quad11^2=121 \\ 2^2=4 & \quad12^2=144\\ 3^2=9 & \quad13 ^2=169\\ 4^2=16 & \quad14^2=196\\ 5^2=25 & \quad15^2=225\\ 6^2=36 & \quad16^2=256\\ 7^ 2=49 & \quad17^2=289\\ 8^2=64 & \quad18^2=324\\ 9^2=81 & \quad19^2=361\\ 10^2=100& \quad20^2= 400\\ \hline \end(masyvas)\]

3 faktas.
Ką galima padaryti su kvadratinėmis šaknimis?
\(\bullet\) Suma arba skirtumas kvadratinės šaknys NELYGUS sumos arba skirtumo kvadratinei šaknims, t.y. \[\sqrt a\pm\sqrt b\ne \sqrt(a\pm b)\] Taigi, jei reikia apskaičiuoti, pavyzdžiui, \(\sqrt(25)+\sqrt(49)\) , tada iš pradžių turite rasti reikšmes \(\sqrt(25)\) ir \(\sqrt (49)\ ) ir sudėkite juos. Vadinasi, \[\sqrt(25)+\sqrt(49)=5+7=12\] Jei reikšmių \(\sqrt a\) arba \(\sqrt b\) nepavyksta rasti pridedant \(\sqrt a+\sqrt b\), tada tokia išraiška toliau nekonvertuojama ir lieka tokia, kokia yra. Pavyzdžiui, sumoje \(\sqrt 2+ \sqrt (49)\) galime rasti \(\sqrt(49)\) - tai yra \(7\) , bet \(\sqrt 2\) negali būti bet kokiu būdu konvertuoti, štai kodėl \(\sqrt 2+\sqrt(49)=\sqrt 2+7\). Be to, šio posakio, deja, jokiu būdu negalima supaprastinti.\(\bullet\) Kvadratinių šaknų sandauga/dalinys yra lygus sandaugos/dalinio kvadratinei šakniai, t.y. \[\sqrt a\cdot \sqrt b=\sqrt(ab)\quad \text(s)\quad \sqrt a:\sqrt b=\sqrt(a:b)\] (su sąlyga, kad abi lygybių dalys turi prasmę)
Pavyzdys: \(\sqrt(32)\cdot \sqrt 2=\sqrt(32\cdot 2)=\sqrt(64)=8\); \(\sqrt(768):\sqrt3=\sqrt(768:3)=\sqrt(256)=16\); \(\sqrt((-25)\cdot (-64))=\sqrt(25\cdot 64)=\sqrt(25)\cdot \sqrt(64)= 5\cdot 8=40\). \(\bullet\) Naudojant šias savybes patogu rasti kvadratines šaknis dideli skaičiai juos faktorinuojant.
Apsvarstykite pavyzdį. Raskite \(\sqrt(44100)\) . Nuo \(44100:100=441\) , tada \(44100=100\cdot 441\) . Pagal dalijimosi kriterijų skaičius \(441\) dalijasi iš \(9\) (nes jo skaitmenų suma yra 9 ir dalijasi iš 9), todėl \(441:9=49\) , tai yra \(441=9\ cdot 49\) .
Taigi, mes gavome: \[\sqrt(44100)=\sqrt(9\cdot 49\cdot 100)= \sqrt9\cdot \sqrt(49)\cdot \sqrt(100)=3\cdot 7\cdot 10=210\] Pažvelkime į kitą pavyzdį: \[\sqrt(\dfrac(32\cdot 294)(27))= \sqrt(\dfrac(16\cdot 2\cdot 3\cdot 49\cdot 2)(9\cdot 3))= \sqrt( \ dfrac(16\cdot4\cdot49)(9))=\dfrac(\sqrt(16)\cdot \sqrt4 \cdot \sqrt(49))(\sqrt9)=\dfrac(4\cdot 2\cdot 7)3 =\dfrac(56)3\]
\(\bullet\) Parodykime, kaip įvesti skaičius po kvadratinės šaknies ženklu, naudojant reiškinio \(5\sqrt2\) pavyzdį (išreiškimo \(5\cdot \sqrt2\) trumpinys). Kadangi \(5=\sqrt(25)\) , tada \ Taip pat atkreipkite dėmesį, kad pvz.
1) \(\sqrt2+3\sqrt2=4\sqrt2\) ,
2) \(5\sqrt3-\sqrt3=4\sqrt3\)
3) \(\sqrt a+\sqrt a=2\sqrt a\) .

Kodėl taip? Paaiškinkime 1 pavyzdžiu). Kaip jau supratote, negalime kažkaip konvertuoti skaičiaus \(\sqrt2\) . Įsivaizduokite, kad \(\sqrt2\) yra koks nors skaičius \(a\) . Atitinkamai, išraiška \(\sqrt2+3\sqrt2\) yra ne kas kita, kaip \(a+3a\) (vienas skaičius \(a\) ir dar trys tokie patys skaičiai \(a\) ). Ir mes žinome, kad tai lygu keturiems tokiems skaičiams \(a\) , tai yra \(4\sqrt2\) .

4 faktas.
\(\bullet\) Dažnai sakoma „negalima išgauti šaknies“, kai neįmanoma atsikratyti šaknies (radikalo) ženklo \(\sqrt () \ \) ieškant kokio nors skaičiaus reikšmės. Pvz., galite įvesti skaičių \(16\), nes \(16=4^2\) , taigi \(\sqrt(16)=4\) . Tačiau iš skaičiaus \(3\) ištraukti šaknį, tai yra, rasti \(\sqrt3\) , neįmanoma, nes nėra tokio skaičiaus, kuris kvadratu duotų \(3\) .
Tokie skaičiai (arba išraiškos su tokiais skaičiais) yra neracionalūs. Pavyzdžiui, skaičiai \(\sqrt3, \ 1+\sqrt2, \ \sqrt(15)\) ir tt yra neracionalūs.
Taip pat neracionalūs yra skaičiai \(\pi\) (skaičius „pi“, maždaug lygus \(3,14\) ), \(e\) (šis skaičius vadinamas Eilerio skaičiumi, apytiksliai lygus \(2 ,7\) ) ir kt.
\(\bullet\) Atminkite, kad bet kuris skaičius bus racionalus arba neracionalus. Ir kartu visi racionalieji ir neracionalūs skaičiai sudaro aibę, vadinamą realiųjų (realiųjų) skaičių rinkinys.Šis rinkinys žymimas raide \(\mathbb(R)\) .
Tai reiškia, kad visi skaičiai, kuriuos šiuo metu žinome, vadinami tikraisiais skaičiais.

5 faktas.
\(\bullet\) Realiojo skaičiaus modulis \(a\) yra neneigiamas skaičius \(|a|\), lygus atstumui nuo taško \(a\) iki \(0\) realiame lange linija. Pavyzdžiui, \(|3|\) ir \(|-3|\) yra lygūs 3, nes atstumai nuo taškų \(3\) ir \(-3\) iki \(0\) yra tas pats ir lygus \(3 \) .
\(\bullet\) Jei \(a\) yra neneigiamas skaičius, tada \(|a|=a\) .
Pavyzdys: \(|5|=5\) ; \(\qquad |\sqrt2|=\sqrt2\) . \(\bullet\) Jei \(a\) yra neigiamas skaičius, tada \(|a|=-a\) .
Pavyzdys: \(|-5|=-(-5)=5\) ; \(\qquad |-\sqrt3|=-(-\sqrt3)=\sqrt3\).
Jie sako, kad neigiamiems skaičiams modulis „suvalgo“ minusą, o teigiamus skaičius, taip pat skaičių \(0\) , modulis palieka nepakitęs.
BETši taisyklė taikoma tik skaičiams. Jei po modulio ženklu turite nežinomą \(x\) (ar kitą nežinomą), pvz., \(|x|\) , apie kurį mes nežinome, ar jis teigiamas, lygus nuliui ar neigiamas, tada Mes negalime atsikratyti modulio. Šiuo atveju ši išraiška išlieka tokia: \(|x|\) . \(\bullet\) Galioja šios formulės: \[(\large(\sqrt(a^2)=|a|))\] \[(\large((\sqrt(a))^2=a)), \text( pateikta ) a\geqslant 0\] Dažnai daroma tokia klaida: sakoma, kad \(\sqrt(a^2)\) ir \((\sqrt a)^2\) yra tas pats dalykas. Tai galioja tik tada, kai \(a\) yra teigiamas skaičius arba nulis. Bet jei \(a\) yra neigiamas skaičius, tai netiesa. Pakanka apsvarstyti tokį pavyzdį. Paimkime skaičių \(-1\) vietoj \(a\). Tada \(\sqrt((-1)^2)=\sqrt(1)=1\) , bet išraiška \((\sqrt (-1))^2\) iš viso neegzistuoja (nes ji yra neįmanoma po šaknies ženklu įdėkite neigiamus skaičius!).
Todėl atkreipiame jūsų dėmesį į tai, kad \(\sqrt(a^2)\) nėra lygus \((\sqrt a)^2\) ! Pavyzdys: 1) \(\sqrt(\left(-\sqrt2\right)^2)=|-\sqrt2|=\sqrt2\), nes \(-\sqrt2<0\) ;

\(\phantom(00000)\) 2) \((\sqrt(2))^2=2\) . \(\bullet\) Kadangi \(\sqrt(a^2)=|a|\) , tada \[\sqrt(a^(2n))=|a^n|\] (išraiška \(2n\) reiškia lyginį skaičių)
Tai yra, išimant šaknį iš skaičiaus, kuris yra tam tikru laipsniu, šis laipsnis sumažinamas perpus.
Pavyzdys:
1) \(\sqrt(4^6)=|4^3|=4^3=64\)
2) \(\sqrt((-25)^2)=|-25|=25\) (atkreipkite dėmesį, kad jei modulis nenustatytas, paaiškėja, kad skaičiaus šaknis yra lygi \(-25) \) ; bet mes prisimename , kuri pagal šaknies apibrėžimą taip negali būti: ištraukdami šaknį visada turime gauti teigiamą skaičių arba nulį)
3) \(\sqrt(x^(16))=|x^8|=x^8\) (kadangi bet koks skaičius iki lyginio laipsnio yra neneigiamas)

6 faktas.
Kaip palyginti dvi kvadratines šaknis?
\(\bullet\) Tiesa kvadratinėms šaknims: jei \(\sqrt a<\sqrt b\) , то \(aPavyzdys:
1) palyginkite \(\sqrt(50)\) ir \(6\sqrt2\) . Pirma, antrąją išraišką paverčiame į \(\sqrt(36)\cdot \sqrt2=\sqrt(36\cdot 2)=\sqrt(72)\). Taigi, nuo \(50<72\) , то и \(\sqrt{50}<\sqrt{72}\) . Следовательно, \(\sqrt{50}<6\sqrt2\) .
2) Tarp kurių sveikųjų skaičių yra \(\sqrt(50)\) ?
Nuo \(\sqrt(49)=7\) , \(\sqrt(64)=8\) ir \(49<50<64\) , то \(7<\sqrt{50}<8\) , то есть число \(\sqrt{50}\) находится между числами \(7\) и \(8\) .
3) Palyginkite \(\sqrt 2-1\) ir \(0,5\) . Tarkime \(\sqrt2-1>0,5\) : \[\begin(sulygiuotas) &\sqrt 2-1>0,5 \ \big| +1\quad \text((pridėkite po vieną prie abiejų pusių))\\ &\sqrt2>0,5+1 \ \big| \ ^2 \quad\text((abejų dalių kvadratas))\\ &2>1,5^2\\ &2>2,25 \end (sulygiuotas)\] Matome, kad gavome neteisingą nelygybę. Todėl mūsų prielaida buvo klaidinga ir \(\sqrt 2-1<0,5\) .
Atkreipkite dėmesį, kad tam tikro skaičiaus pridėjimas prie abiejų nelygybės pusių neturi įtakos jos ženklui. Abiejų nelygybės dalių padauginimas/dalinimas iš teigiamo skaičiaus taip pat neturi įtakos jos ženklui, tačiau padauginus/dalijus iš neigiamo skaičiaus nelygybės ženklas apverčiamas!
Abi lygties/nelygybės pusės gali būti padalytos kvadratu TIK JEI abi pusės yra neneigiamos. Pavyzdžiui, nelygybėje iš ankstesnio pavyzdžio galite kvadratuoti abi puses, nelygybėje \(-3<\sqrt2\) нельзя (убедитесь в этом сами)! \(\bullet\) Atkreipkite dėmesį \[\begin (sulygiuotas) &\sqrt 2\apytiksliai 1,4\\ &\sqrt 3\apytiksliai 1,7 \pabaiga (sulygiuotas)\] Apytikslės šių skaičių reikšmės žinojimas padės lyginant skaičius! \(\bullet\) Norėdami išgauti šaknį (jei ji išskirta) iš kokio nors didelio skaičiaus, kurio nėra kvadratų lentelėje, pirmiausia turite nustatyti, tarp kurių „šimtų“ jis yra, tada tarp kurių „dešimties“, ir tada nustatykite paskutinį šio skaičiaus skaitmenį. Parodykime, kaip tai veikia pavyzdžiu.
Paimkite \(\sqrt(28224)\) . Žinome, kad \(100^2=10\,000\) , \(200^2=40\,000\) ir pan. Atminkite, kad \(28224\) yra tarp \(10\,000\) ir \(40\,000\) . Todėl \(\sqrt(28224)\) yra tarp \(100\) ir \(200\) .
Dabar nustatykime, tarp kurių „dešimties“ yra mūsų skaičius (ty, pavyzdžiui, tarp \(120\) ir \(130\) ). Iš kvadratų lentelės taip pat žinome, kad \(11^2=121\) , \(12^2=144\) ir tt, tada \(110^2=12100\) , \(120^2=14400 \ ) , \(130^2=16900\) , \(140^2=19600\) , \(150^2=22500\) , \(160^2=25600\) , \(170^2=28900\) ). Taigi matome, kad \(28224\) yra tarp \(160^2\) ir \(170^2\) . Todėl skaičius \(\sqrt(28224)\) yra tarp \(160\) ir \(170\) .
Pabandykime nustatyti paskutinį skaitmenį. Prisiminkime, kokius vienaženklius skaičius kvadratu duoda pabaigoje \ (4 \) ? Tai yra \(2^2\) ir \(8^2\) . Todėl \(\sqrt(28224)\) baigsis 2 arba 8. Patikrinkime tai. Raskite \(162^2\) ir \(168^2\) :
\(162^2=162\cdot 162=26224\)
\(168^2=168\cdot 168=28224\) .
Taigi \(\sqrt(28224)=168\) . Voila!

Norint tinkamai išspręsti matematikos egzaminą, pirmiausia reikia išstudijuoti teorinę medžiagą, kurioje pateikiama daugybė teoremų, formulių, algoritmų ir kt. Iš pirmo žvilgsnio gali pasirodyti, kad tai gana paprasta. Tačiau rasti šaltinį, kuriame vieningo valstybinio matematikos egzamino teorija būtų lengvai ir suprantamai pateikiama bet kokio lygio mokiniams, iš tikrųjų yra gana sudėtinga užduotis. Mokykliniai vadovėliai ne visada gali būti po ranka. O rasti pagrindines matematikos egzamino formules gali būti sunku net internete.

Kodėl taip svarbu mokytis matematikos teorijos, o ne tik tiems, kurie laiko egzaminą?

1. Nes tai praplečia akiratį. Matematikos teorinės medžiagos studijavimas naudingas kiekvienam, norinčiam gauti atsakymus į įvairiausius klausimus, susijusius su pasaulio pažinimu. Gamtoje viskas sutvarkyta ir turi aiškią logiką. Būtent tai atsispindi moksle, per kurį galima suprasti pasaulį.
2. Nes lavina intelektą. Studijuodamas matematikos egzamino informacinę medžiagą, taip pat spręsdamas įvairias problemas, žmogus išmoksta logiškai mąstyti ir mąstyti, teisingai ir aiškiai formuluoti mintis. Jis ugdo gebėjimą analizuoti, apibendrinti, daryti išvadas.

Kviečiame asmeniškai įvertinti visus mūsų požiūrio į mokomosios medžiagos sisteminimą ir pateikimą privalumus.

Gėlių šaknų padalijimas yra tiesiog būtinas, jei nuspręsite iš karto gauti porą stiprių ir subrendusių augalų, kurie bus paruošti žydėjimui ateityje per vieną „įvykį“. Bet jei pažvelgsime į šią problemą kitu kampu, galime pasakyti, kad šaknų padalijimas gali neigiamai paveikti augalų būklę, ypač jei šaknys nėra tinkamai tvarkomos.

Prieš analizuojant klausimą – kaip padalinti šaknis, reikia apsispręsti, kokius augalus galima dauginti tokiu būdu. Visų pirma, tai yra žoliniai egzemplioriai su gera šaknų sistema. Taip galima skirstyti gėles ir krūmus.

Šaknų padalijimo algoritmas:

1. Nuimkite gėlę nuo žemės ir nukratykite didelį žemės grumstą.

2. Likusią žemę nuplaukite vandeniu, tačiau visiškai išvalyti šaknų nereikia, svarbiausia, kad dalijant žemė jums netrukdytų.

4. Apkarpykite ūglius iki 10 cm aukščio Šis renginys padės panaudoti gėlių jėgas atstatyti šaknis, o ne ūglių augimą.

5. Jei šaknų procesai pradėjo kietėti, ir aišku, kad nieko gero iš jų nebus, tai šios šaknys nupjaunamos.

6. Geltoni ir sausi ūgliai, lapai iš karto sunaikinami.

7. Atkreipkite dėmesį į tai, kad centrinė gėlės dalis neturėtų būti padalinta. Atskirkite tik šonines šaknis.

8. Pjūviai apdorojami anglimi, o nauji augalai sodinami į specialius vazonus.

Ką dar reikėtų žinoti apie šaknų dalijimąsi?

Neatlikite šio proceso, kol augalas žydi. Geriau jį išleisti pasibaigus šiam laikotarpiui. Jei sunku laikytis šios rekomendacijos, likus porai dienų iki proceso, pumpurai ir žiedai sunaikinami, kitaip gėlė negalės įsišaknyti.

Krūmas atviroje dirvoje skirstomas rudenį, o kambarinės gėlės – pavasarį. Prieš išimant augalą nuo žemės, dirva gerai palaistoma, kad nebūtų pažeista šaknų sistema. Jokiu būdu netraukite augalo už antžeminės dalies. Šaknų sistema išimama kartu su dirvožemiu, beldžiama į puodą. Jei gėlė auga gėlių lovoje, ji atsargiai iškasama ir išimama sodo įrankiais. Siekiant sumažinti šaknų sistemos pažeidimą, naudojamas aštrus peilis. Nelaužykite šaknų sistemos rankomis! Tai neigiamai paveiks būsimos gėlės būklę.

Pastaba! Neskaidykite krūmo į mažas dalis, nes tai gali neigiamai paveikti jų augimą ir vystymąsi. Išgyvenimas bus minimalus. Nepamirškite, kad ant kiekvienos dalies turi būti po vieną suaugusiojo ūglį.

Negalima iš karto sodinti augalų į atvirą dirvą, nes jiems reikia atsigavimo laikotarpio, o saulės spinduliai neigiamai paveiks augalus.

Dauginimo dalijant krūmą nauda

Be to, kad augalų yra daugiau, jie dar ir atjauninami. Juk beprasmiška ginčytis su tuo, kad visų gyvų būtybių biologinis amžius nėra amžinas, o augalas – ne išimtis. Taigi galite atnaujinti savo daugiamečius augalus, padalindami šaknis be papildomų sodinukų.

Augalų dauginimas dalijant šaknis yra vienas iš patogiausių būdų, nes viena operacija leidžia iš karto gauti kelis subrendusius ir stiprius augalus, paruoštus žydėti ar derėti. Kita vertus, šis metodas tinka ne visoms kultūroms, o netinkamai atliktas gali pakenkti visam augalui.

Dalijant šaknį, dauginami krūmai ir žoliniai augalai su išsivysčiusia šaknų sistema su pumpurų formavimu. Šiai kategorijai priklauso lazdynas, alyvinė, kuri yra krūmas, orchidėjos, chrizantemos, delfinijos ir bijūnai, taip pat daugelis kitų gėlių.

Pagrindiniai procedūros etapai:

• Atsargiai išimkite augalą iš dirvos ir standžiu šepečiu nukratykite žemės rutulį.
• Likusią žemę nuplaukite kambario temperatūros vandeniu, panardindami šaknis į vandens indą. Nebūtina nuplauti visos žemės, svarbiausia, kad dirvožemis netrukdytų dalytis.
• Apskaičiuokite, kiek augalų galima gauti iš šio krūmo, pasirinkdami pagrindinius suaugusius ūglius ir aktyvius pumpurus.
• Nupjaukite visus augalo ūglius iki dešimties centimetrų aukščio (būtina aukštiems žoliniams augalams ir krūmams). Tai leis augalui panaudoti energiją šaknų sistemai atkurti, neišleisdamas jos antžeminėms dalims maitinti.
• Jei yra sumedėjusių ūglių, pavyzdžiui, dauginant rožes, jie nupjaunami iki pat šaknies.
• Pašalinami visi pažeisti ir pageltę ūgliai bei lapai.
• Įsitikinkite, kad pjūviai, atskirdami šonines krūmo dalis. Centrinė augalo dalis neturėtų būti padalinta.
• Pjūvius apdorokite medžio anglimi, naujus augalus pasodinkite į paruoštus konteinerius ir laistykite augimą stimuliuojančiu tirpalu.

Ką reikia žinoti dalijant krūmą

Žydėjimo metu tokiu būdu dauginti negalima. Geriausia išsiskirstyti pasibaigus šiam laikotarpiui. Jei tai sunku, likus dviem dienoms iki dalijimo, nupjaunami visi žiedai ir pumpurai. Priešingu atveju augalas gali mirti.

Kambarines gėles geriausia dalyti kovo mėnesį ramybės periodo pabaigoje, o atvirame lauke augančius krūmus – rudenį prieš prasidedant šalnoms.

Dalijimosi metu šaknų sistema turi būti aiškiai matoma ir lengvai atskiriama nuo žemės. Kad ištraukimo metu nebūtų pažeistos šaknys, dieną prieš dalijimą dirva gerai sudrėkinama. Netraukite už anteninės augalo dalies. Šaknys su žemišku grumstu išimamos bakstelėjus į gėlių vazoną. Jei augalas yra gėlių lovoje, atsargiai išskobkite jį sodo mentele ir kietu dažų teptuku.

Aštriu peiliu padalijama šaknis, kad augalai būtų kuo mažiau sužaloti. Sodo žirklių geriau nenaudoti, nes jos gali suglamžyti šaknų dalis. Jūs negalite sulaužyti šaknų rankomis!

Nedalykite augalo į per mažas dalis - tai gali pakenkti visam krūmui, nes išgyvenamumas bus daug mažesnis. Kiekviena dalis turi turėti subrendusį ūglį.

Padalytų augalų nepatartina iš karto sodinti į atvirą žemę, nes jiems reikalingas atsigavimo laikotarpis ir tiesioginiai saulės spinduliai, taip pat kenkėjai ir ligos jiems bus pavojingi, todėl naujus sodinukus geriau atlaikyti saugomoje žemėje porai. savaičių. Pastarasis turi būti sterilus ir tinkamas dalijamo augalo augimo sąlygoms.

Kam naudojamas krūmo padalijimas

Be egzempliorių skaičiaus didinimo, šaknų padalijimo metodas taikomas kompleksiniam augalų, kurių biologinis amžius eina į pabaigą, atjauninimui. Taip galite atnaujinti daugiamečius augalus neaugindami sodinukų.

Šis būdas labai efektyvus, jei reikia išsaugoti motininio augalo dekoratyvines savybes, kurios gali būti prarastos naudojant kitus dauginimo būdus.

Dauginimosi padalijus šaknį pavyzdžiai:

Vaizdo įrašas 1. Phalaenopsis orchidėjų dauginimas

Video 3. Serbentų dauginimas dalijant krūmą

Atėjo laikas išardyti šaknų ištraukimo metodai. Jie pagrįsti šaknų savybėmis, visų pirma lygybe, kuri galioja bet kuriam neneigiamam skaičiui b.

Žemiau mes savo ruožtu apsvarstysime pagrindinius šaknų išgavimo būdus.

Pradėkime nuo paprasčiausio atvejo – šaknų ištraukimas iš natūraliųjų skaičių naudojant kvadratų lentelę, kubelių lentelę ir kt.

Jei lentelės iš kvadratų, kubelių ir kt. nėra po ranka, logiška naudoti šaknies išskyrimo metodą, kuris apima šaknies skaičiaus skaidymą į paprastus veiksnius.

Atskirai verta pasilikti, o tai įmanoma šaknims su nelyginiais rodikliais.

Galiausiai apsvarstykite metodą, leidžiantį nuosekliai rasti šaknies vertės skaitmenis.

Pradėkime.

Naudojant kvadratų lentelę, kubelių lentelę ir kt.

Paprasčiausiais atvejais šaknis leidžia išgauti kvadratų, kubelių ir pan. Kas yra šios lentelės?

Sveikųjų skaičių nuo 0 iki 99 imtinai kvadratų lentelė (parodyta žemiau) susideda iš dviejų zonų. Pirmoji lentelės zona yra pilkame fone, pasirinkus tam tikrą eilutę ir stulpelį, galima padaryti skaičių nuo 0 iki 99. Pavyzdžiui, pasirinkime 8 dešimčių eilutę ir 3 vienetų stulpelį, taip pataisydami skaičių 83. Antroji zona užima likusią stalo dalį. Kiekvienas jo langelis yra tam tikros eilutės ir stulpelio sankirtoje ir yra atitinkamo skaičiaus kvadratas nuo 0 iki 99. Mūsų pasirinktos 8 dešimčių eilutės ir 3 stulpelio vieneto sankirtoje yra langelis su skaičiumi 6889, kuris yra skaičiaus 83 kvadratas.

Kubų lentelės, skaičių nuo 0 iki 99 ketvirtųjų laipsnių lentelės ir panašios į kvadratų lentelę, tik jose antroje zonoje yra kubai, ketvirtosios laipsniai ir pan. atitinkamus skaičius.

Kvadratų, kubelių, ketvirtųjų laipsnių lentelės ir kt. leidžia išgauti kvadratines šaknis, kubines šaknis, ketvirtąsias šaknis ir kt. atitinkamai iš skaičių šiose lentelėse. Paaiškinkime jų taikymo principą išgaunant šaknis.

Tarkime, kad iš skaičiaus a reikia išskirti n-ojo laipsnio šaknį, o skaičius a yra n-ųjų laipsnių lentelėje. Pagal šią lentelę skaičių b randame tokį, kad a=b n . Tada , todėl skaičius b bus norima n-ojo laipsnio šaknis.

Kaip pavyzdį parodykime, kaip naudojant kubo lentelę išgaunama 19683 kubo šaknis. Kubų lentelėje randame skaičių 19 683, iš jo nustatome, kad šis skaičius yra skaičiaus 27 kubas, todėl .

Aišku, kad n-ųjų laipsnių lentelės yra labai patogios išimant šaknis. Tačiau jų dažnai nėra po ranka, o jų sudarymas reikalauja tam tikro laiko. Be to, dažnai reikia išgauti šaknis iš skaičių, kurių nėra atitinkamose lentelėse. Tokiais atvejais tenka griebtis kitų šaknų išgavimo būdų.

Šakninio skaičiaus išskaidymas į pirminius veiksnius

Gana patogus būdas ištraukti šaknį iš natūraliojo skaičiaus (jei, žinoma, šaknis išskirta), yra šaknies skaičių išskaidyti į pirminius veiksnius. Jo esmė tokia: po to gana lengva jį pavaizduoti kaip laipsnį su norimu rodikliu, kuris leidžia gauti šaknies reikšmę. Paaiškinkime šį dalyką.

Tegu n-ojo laipsnio šaknis išskiriama iš natūraliojo skaičiaus a, o jo reikšmė lygi b. Šiuo atveju lygybė a=b n yra teisinga. Skaičius b kaip bet koks natūralusis skaičius gali būti pavaizduotas kaip visų jo pirminių faktorių p 1 , p 2 , …, p m sandauga forma p 1 p 2 … p m , o šakninis skaičius a šiuo atveju pavaizduotas kaip (p 1 p 2 ... p m) n . Kadangi skaičiaus išskaidymas į pirminius veiksnius yra unikalus, šakninio skaičiaus a išskaidymas į pirminius veiksnius atrodys taip (p 1 ·p 2 ·…·p m) n , o tai leidžia apskaičiuoti šaknies reikšmę kaip .

Atkreipkite dėmesį, kad jei šaknies skaičiaus a faktorizacija negali būti pavaizduota forma (p 1 ·p 2 ·…·p m) n , tai n-ojo laipsnio šaknis iš tokio skaičiaus a nėra visiškai išskirta.

Spręskime pavyzdžius.

Pavyzdys.

Paimkite kvadratinę šaknį iš 144 .

Sprendimas.

Jei atsigręžtume į ankstesnėje pastraipoje pateiktą kvadratų lentelę, aiškiai matyti, kad 144=12 2 , iš kurios aišku, kad 144 kvadratinė šaknis yra 12 .

Tačiau atsižvelgiant į tai, mus domina, kaip šaknis išgaunama išskaidžius šaknies skaičių 144 į pirminius veiksnius. Pažvelkime į šį sprendimą.

Išskaidykime 144 prie pagrindinių veiksnių:

Tai yra, 144 = 2 2 2 2 3 3 . Remiantis gautu skaidymu, gali būti atliekamos šios transformacijos: 144 = 2 2 2 2 3 3 = (2 2) 2 3 2 = (2 2 3) 2 = 12 2. Vadinasi, .

Naudojant šaknų laipsnio ir savybių savybes, tirpalą būtų galima suformuluoti kiek kitaip: .

Atsakymas:

Norėdami konsoliduoti medžiagą, apsvarstykite dar dviejų pavyzdžių sprendimus.

Pavyzdys.

Apskaičiuokite šaknies vertę.

Sprendimas.

Šakninio skaičiaus 243 pirminis faktorius yra 243=3 5 . Šiuo būdu, .

Atsakymas:

Pavyzdys.

Ar šaknies reikšmė yra sveikas skaičius?

Sprendimas.

Norėdami atsakyti į šį klausimą, išskaidykime šakninį skaičių į pirminius veiksnius ir pažiūrėkime, ar jį galima pavaizduoti kaip sveikojo skaičiaus kubą.

Turime 285 768=2 3 3 6 7 2 . Gautas skilimas nevaizduojamas kaip sveikojo skaičiaus kubas, nes pirminio koeficiento 7 laipsnis nėra trijų kartotinis. Todėl 285 768 kubo šaknis nėra visiškai paimta.

Atsakymas:

Nr.

Šaknų ištraukimas iš trupmeninių skaičių

Atėjo laikas išsiaiškinti, kaip šaknis išgaunama iš trupmeninio skaičiaus. Tegul trupmeninės šaknies skaičius užrašomas kaip p/q . Pagal koeficiento šaknies savybę teisinga tokia lygybė. Iš šios lygybės išplaukia trupmenos šaknies taisyklė: trupmenos šaknis yra lygi skaitiklio šaknies dalijimo iš vardiklio šaknies koeficientui.

Pažvelkime į šaknies ištraukimo iš trupmenos pavyzdį.

Pavyzdys.

Kokia yra bendrosios trupmenos 25/169 kvadratinė šaknis.

Sprendimas.

Pagal kvadratų lentelę matome, kad pradinės trupmenos skaitiklio kvadratinė šaknis yra 5, o vardiklio kvadratinė šaknis yra 13. Tada . Tai užbaigia šaknies ištraukimą iš įprastos frakcijos 25/169.

Atsakymas:

Dešimtainės trupmenos arba mišraus skaičiaus šaknis išgaunama pakeitus šaknies skaičius paprastosiomis trupmenomis.

Pavyzdys.

Paimkite dešimtainio skaičiaus 474.552 kubinę šaknį.

Sprendimas.

Pradinį dešimtainį skaičių pavaizduokime kaip bendrąją trupmeną: 474.552=474552/1000 . Tada . Belieka išskirti kubo šaknis, kurios yra gautos trupmenos skaitiklyje ir vardiklyje. Nes 474 552=2 2 2 3 3 3 13 13 13=(2 3 13) 3 = 78 3 ir 1 000 = 10 3 , tada ir . Belieka tik užbaigti skaičiavimus .

Atsakymas:

.

Neigiamojo skaičiaus šaknies ištraukimas

Atskirai verta pasilikti ties šaknų ištraukimu iš neigiamų skaičių. Tyrinėdami šaknis sakėme, kad kai šaknies rodiklis yra nelyginis skaičius, tada neigiamas skaičius gali būti po šaknies ženklu. Tokiems žymenims suteikėme tokią reikšmę: neigiamam skaičiui −a ir nelyginiam šaknies 2 n−1 rodikliui turime . Ši lygybė suteikia nelyginių šaknų ištraukimo iš neigiamų skaičių taisyklė: norėdami išskirti šaknį iš neigiamo skaičiaus, turite ištraukti šaknį iš priešingo teigiamo skaičiaus ir prieš rezultatą įdėti minuso ženklą.

Panagrinėkime sprendimo pavyzdį.

Pavyzdys.

Raskite šakninę vertę.

Sprendimas.

Transformuokime pradinę išraišką taip, kad po šaknies ženklu atsirastų teigiamas skaičius: . Dabar mišrų skaičių pakeičiame įprasta trupmena: . Taikome šaknies ištraukimo iš paprastosios trupmenos taisyklę: . Belieka apskaičiuoti gautos trupmenos skaitiklio ir vardiklio šaknis: .

Čia yra sprendimo santrauka: .

Atsakymas:

.

Bitiškai šakninės vertės radimas

Paprastai po šaknimi yra skaičius, kuris, naudojant aukščiau aptartus metodus, negali būti vaizduojamas kaip bet kurio skaičiaus n-asis laipsnis. Tačiau tuo pat metu reikia žinoti tam tikros šaknies vertę, bent jau iki tam tikro ženklo. Tokiu atveju, norėdami išgauti šaknį, galite naudoti algoritmą, leidžiantį nuosekliai gauti pakankamą norimo skaičiaus skaitmenų reikšmių skaičių.

Pirmasis šio algoritmo žingsnis yra išsiaiškinti, kas yra svarbiausias šakninės reikšmės bitas. Norėdami tai padaryti, skaičiai 0, 10, 100, ... paeiliui didinami iki laipsnio n, kol gaunamas skaičius, viršijantis šakninį skaičių. Tada skaičius, kurį ankstesniame žingsnyje padidinome iki laipsnio n, parodys atitinkamą aukštą eilę.

Pavyzdžiui, apsvarstykite šį algoritmo veiksmą, kai ištraukite kvadratinę šaknį iš penkių. Paimame skaičius 0, 10, 100, ... ir statome juos kvadratu, kol gauname didesnį už 5 skaičių. Turime 0 2 = 0<5 , 10 2 =100>5 , o tai reiškia, kad reikšmingiausias skaitmuo bus vieneto skaitmuo. Šio bito, kaip ir mažesnių, reikšmė bus rasta kituose šaknies ištraukimo algoritmo žingsniuose.

Visais sekančiais algoritmo žingsniais siekiama paeiliui patikslinti šaknies reikšmę dėl to, kad randamos norimos šaknies reikšmės kitų skaitmenų reikšmės, pradedant nuo didžiausios ir pereinant prie mažiausios. . Pavyzdžiui, šaknies reikšmė pirmame žingsnyje yra 2 , antrajame - 2,2 , trečiame - 2,23 ir tt 2,236067977 ... . Apibūdinkime, kaip randamos bitų reikšmės.

Bitai randami išvardijant galimas jų reikšmes 0, 1, 2, ..., 9. Šiuo atveju lygiagrečiai skaičiuojami atitinkamų skaičių n-ieji laipsniai ir lyginami su šaknies skaičiumi. Jei tam tikru etapu laipsnio reikšmė viršija radikalų skaičių, tada skaitmens, atitinkančio ankstesnę reikšmę, reikšmė laikoma rasta ir pereinama prie kito šaknies išskyrimo algoritmo žingsnio, jei tai neįvyksta, tada šio skaitmens reikšmė yra 9 .

Paaiškinkime visus šiuos taškus naudodami tą patį penkių kvadratinės šaknies ištraukimo pavyzdį.

Pirmiausia suraskite vieneto skaitmens reikšmę. Kartosime reikšmes 0, 1, 2, …, 9, atitinkamai apskaičiuodami 0 2, 1 2, …, 9 2, kol gausime reikšmę, didesnę už radikalų skaičių 5. Visi šie skaičiavimai yra patogiai pateikti lentelės pavidalu:

Taigi vienetų skaitmens reikšmė yra 2 (nes 2 2<5 , а 2 3 >5). Pereikime prie dešimtos vietos vertės nustatymo. Tokiu atveju skaičius 2.0, 2.1, 2.2, ..., 2.9 padalinsime kvadratu, gautas reikšmes lygindami su šaknies skaičiumi 5:

Nuo 2.2 2<5 , а 2,3 2 >5 , tada dešimtos vietos reikšmė yra 2 . Galite pradėti ieškoti šimtosios vietos vertės:

Taigi randama kita penkių šaknies reikšmė, ji lygi 2,23. Taigi galite toliau ieškoti vertybių: 2,236, 2,2360, 2,23606, 2,236067, … .

Norėdami konsoliduoti medžiagą, mes analizuosime šaknies ištraukimą šimtųjų dalių tikslumu, naudodami nagrinėjamą algoritmą.

Pirmiausia apibrėžiame vyresnįjį skaitmenį. Norėdami tai padaryti, supjaustome skaičius 0, 10, 100 ir kt. kol gausime skaičių didesnį už 2151.186 . Turime 0 3 = 0<2 151,186 , 10 3 =1 000<2151,186 , 100 3 =1 000 000>2 151.186 , todėl reikšmingiausias skaitmuo yra dešimties skaitmuo.

Apibrėžkime jo vertę.

Nuo 103<2 151,186 , а 20 3 >2 151,186 , tada dešimties skaitmens reikšmė yra 1 . Pereikime prie vienetų.

Taigi vienos vietos vertė yra 2 . Pereikime prie dešimties.

Kadangi net 12,9 3 yra mažesnis už radikalųjį skaičių 2 151,186 , dešimtosios vietos reikšmė yra 9 . Belieka atlikti paskutinį algoritmo žingsnį, jis mums duos šaknies reikšmę reikiamu tikslumu.

Šiame etape šaknies vertė randama iki šimtųjų dalių: .

Baigdamas šį straipsnį norėčiau pasakyti, kad yra daug kitų būdų išgauti šaknis. Tačiau daugeliui užduočių pakanka tų, kurias išnagrinėjome aukščiau.

Bibliografija.

• Makarychev Yu.N., Mindyuk N.G., Neshkov K.I., Suvorova S.B. Algebra: vadovėlis 8 langeliams. švietimo įstaigų.
• Kolmogorovas A.N., Abramovas A.M., Dudnicinas Yu.P. ir kt.. Algebra ir analizės užuomazgos: vadovėlis bendrojo lavinimo įstaigų 10-11 klasei.
• Gusevas V.A., Mordkovičius A.G. Matematika (vadovas stojantiesiems į technikos mokyklas).

Pavyzdžiui, tarkime, kad turime išgauti kvadratinę šaknį iš trupmenos 25/144. 6. Apytikslis kvadratinių šaknų ištraukimas. Jeigu D

Norėdami išgauti kvadratinę sveikojo skaičiaus šaknį 1 tikslumu, turite išgauti, kaip įprasta, ir atmesti likusią dalį, gautą operacijos pabaigoje. Norėdami apytiksliai ištraukti šaknį iš trupmenos, pirmiausia turite padaryti vardiklį tobulu kvadratu.

Ankstesnėse pamokose supratome, kas yra kvadratinė šaknis. Ir sugalvojo, kaip padauginti šaknis. Mes išardėme formulę šaknų dauginimui iš krumpliaračių.

Formulė tokia paprasta, kaip daugyba. Galimybių šaknų padalijimo formulė nėra tokia plati kaip daugybos formulė. Šiame pavyzdyje šaknų padalijimas padėjo mums gauti gerą atsakymą. Yra ir sudėtingesnių transformacijų.

• Darbų katalogas
• Klausimai ir atsakymai

Tik tam, kad būtų naudojama šaknų padalijimo formulė. Apsvarstykite formulę, kaip padalinti šaknis priešinga kryptimi. Mūsų atveju tokia šaknų padalijimo formuluotė labai padeda išgauti šaknis iš frakcijų!

Jokiu problemu! Jei negalite iš karto išgauti šaknies, išverskite dešimtainę trupmeną į paprastąją ir pirmyn! Teisingai! Sumaišytą skaičių verčiame į netinkamą trupmeną - ir pagal žinomą šaknų padalijimo formulę!

Tikiuosi, kad šaknų pasidalijimas nėra problema. Panagrinėkime paskutinę kvadratinių šaknų savybę. Jau bus tam tikrų subtilybių ir spąstų. Ši savybė trumpai vadinama kvadratine šaknimi. Kodėl gi ne? Padauginkite šaknį iš savęs – taip, viskas! Ir ne tik aikštėje galima. Bet kokiu laipsniu.

Tai yra skaičius, kurį patraukus kvadratu, jis turėtų duoti dviženklį. Pagal šių veiksmų taisykles mes patys aikštėje prikeliame originalią išraišką prie šaknų ir viską apskaičiuojame. Mes tai darome su bet kokiu šaknies laipsniu iš bet kurios išraiškos, ir viskas bus mums apskaičiuota, supaprastinta ir sėkminga.

Visuose vadovėliuose, žinynuose ir žinynuose prie tokios formulės visada rašoma: „kur a yra didesnis už nulį arba lygus jam“. Šiuose žodžiuose, kuriuos daugelis tiesiog praleidžia, slypi pagrindiniai šaknų sunkumai. Taigi, kur šaknyse gali atsirasti neigiami skaičiai ir išraiškos?

Ištraukiame šaknį iš keturių ir gauname 2. Kadangi aritmetinė kvadratinė šaknis (o mokykloje dirbame tik su tokia!) visada yra neneigiamas skaičius! Tai paskutinė, trečioji šaknų savybė.

• Algebra
• 14 taškų

Čia tai reiškia tik tai, kad bet kuriam a ženklui šaknies ištraukimo iš kvadrato rezultatas visada bus neneigiamas. Jei x Tiesą sakant, tai yra pagrindinis sunkumas dirbant su šaknimis. Skirtingai nei paprastesnėse matematikos dalyse, čia teisingas atsakymas dažnai automatiškai neišplaukia iš formulių.

Pagrindiniai praktiniai patarimai dirbant su kvadratinėmis šaknimis. Jei po šaknies ženklu yra minusas, toliau negalite nuspręsti. Jei po šaknimi viskas gerai, pliusas, o ištraukus gaunamas sąmoningas minusas - padaryk iš to pliusą! To reikalauja veiksmų su kvadratinėmis šaknimis taisyklės.

24 padalintas iš 7+1 šaknų

Visos šaknų savybės yra susijusios su daugyba-dalyba. Nėra specialių formulių, kaip pridėti ir atimti šaknis! Nors tas pačias šaknis, žinoma, galima pridėti ir atimti. Tačiau šie veiksmai neturi nieko bendra su specifinėmis šaknų savybėmis.

Puikiai. Šaknys nėra jūsų problema. Jokiu problemu! Einame į Specialų skyrių 555. Kvadratinės šaknys. Ten pateikti visi paaiškinimai. Šiame skyriuje susipažinsite su praktiniu darbu su šaknimis. Diskriminantas yra išraiška, nuo kurios priklauso duotosios lygties šaknų skaičius.

Sumažinkime kosinuso laipsnį pagal formulę: 1+cos2α=2cos2α. Todėl šaknų nėra. Šiuo atveju trinaris 4y2-2y+5 įims tik teigiamas bet kurios y vertės reikšmes.

IŠJUNGTA: pi skaičius, padalytas iš 3 šaknies, arba 1C slapyvardžio matematika

Juk jei dviejų radikalų skirtumą padauginsime iš jų sumos, tai bus gautas šaknų kvadratų skirtumas, t.y. gausite išraišką be radikalių ženklų. 1) Antrojo veiksnio šakninę išraišką pavaizduojame kaip dviejų išraiškų sumos kvadratą, t.y. forma (a + b)2. Tai leis mums išgauti aritmetinę kvadratinę šaknį.

GALIOJIMO IŠPLĖSTIMAS. Primenu: čia a yra neneigiamas skaičius (didesnis už nulį arba lygus jam), b yra teigiamas (didesnis už nulį)! Kitaip formulė neturi prasmės... Dabar mūsų arsenale yra dvi formulės.

Bet kaip tik šie veiksmai sukelia daug problemų... Su tuo reikia žiūrėti nuodugniai. Jokiu problemu! Nebent, žinoma, žinote veiksmus, turinčius galių... Turėkime gerą skaičių 2. Padėkime kvadratu. Pakelkime savo laipsnį į aikštę.

Ką daryti, jei laipsnis yra nelyginis? Viskas paprasta. Tačiau iki šiol dirbome tik su neneigiamais skaičiais ir išraiškomis. Čia viskas aišku ir paprasta. Ši formulė neveikia esant neigiamoms reikšmėms.

Mes žinome, kaip iš darbo ištraukti šaknį. Kvadratinė šaknis yra paprastas dalykas. Tai atsitinka dar šauniau, kai reikia paimti mišraus skaičiaus šaknį! O dabar praktikuokime šaknis. Labai paprasta. Tiesiogiai šaknies prasme. Kokia, pavyzdžiui, yra dviejų kvadratinė šaknis?