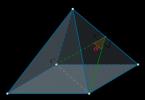
Що називають лінійним кутом двогранного кута. Конспект уроку з математики "Двогранний кут". Захист персональної інформації

$\blacktriangleright$ Двогранний кут - кут, утворений двома напівплощинами і прямою $a$ , яка є їх спільним кордоном.

$\blacktriangleright$ Щоб знайти кут між площинами $\xi$ і $\pi$ потрібно знайти лінійний кут (причому гострийабо прямий) двогранного кута, утвореного площинами $\xi$ і $\pi$ :

Крок 1: нехай $\xi\cap\pi=a$ (лінія перетину площин). У площині $\xi$ відзначимо довільну точку $F$ і проведемо $FA\perp a$;

Крок 2: проведемо (FG perp );

Крок 3: за ТТП ((FG) – перпендикуляр, (FA) – похила, (AG) – проекція) маємо: (AG perpa);

Крок 4: кут $\angle FAG$ називається лінійним кутом двогранного кута, утвореного площинами $\xi$ і $\pi$ .

Зауважимо, що трикутник (AG) - прямокутний.
Зауважимо також, що площина (AFG), побудована таким чином, перпендикулярна обох площин ((xi)) і (pi). Отже, можна сказати інакше: кут між площинами$\xi$ і $\pi$ - це кут між двома пересічними прямими $c\in \xi$ і $b\in\pi$ , що утворюють площину, перпендикулярну і $\xi$ ) і $\pi$ .

Завдання 1 #2875

Рівень завдання: Складніше ЄДІ

Дано чотирикутну піраміду, всі ребра якої рівні, причому основа є квадратом. Знайдіть $6\cos \alpha$ , де $\alpha$ - кут між її суміжними бічними гранями.

Нехай $SABCD$ - дана піраміда ($S$ - вершина), ребра якої рівні $a$. Отже, всі бічні грані є рівними рівносторонні трикутники. Знайдемо кут між гранями (SAD) і (SCD).

Проведемо $CH\perp SD$. Так як $\triangle SAD=\triangle SCD$, то $AH$ також буде висотою $\triangle SAD$ . Отже, за визначенням $\angle AHC=\alpha$ - лінійний кут двогранного кута між гранями $SAD$ і $SCD$.
Так як в основі лежить квадрат, то (AC = a sqrt2). Зауважимо також, що $CH=AH$ - висота рівностороннього трикутника зі стороною $a$, отже, $CH=AH=\frac(\sqrt3)2a$ .
Тоді за теоремою косінусів з $\triangle AHC$ : \[\cos \alpha=\dfrac(CH^2+AH^2-AC^2)(2CH\cdot AH)=-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\]

Відповідь: -2

Завдання 2 #2876

Рівень завдання: Складніше ЄДІ

Площини $\pi_1$ і $\pi_2$ перетинаються під кутом, косинус якого дорівнює $0,2$. Площини $\pi_2$ і $\pi_3$ перетинаються під прямим кутом, причому лінія перетину площин $\pi_1$ і $\pi_2$ паралельна лінії перетину площин $\pi_2$ і $\ pi_3 $. Знайдіть синус кута між площинами $\pi_1$ і $\pi_3$ .

Нехай лінія перетину $\pi_1$ і $\pi_2$ - пряма $a$ , лінія перетину $\pi_2$ і $\pi_3$ - пряма $b$ , а лінія перетину $\pi_3$ та $\pi_1$ - пряма $c$ . Оскільки $a\parallel b$ , то $c\parallel a\parallel b$ (за теоремою з розділу теоретичної довідки "Геометрія в просторі" (rightarrow\) "Введення в стереометрію, паралельність").

Зазначимо точки $A\in a, B\in b$ так, щоб $AB\perp a, AB\perp b$ (це можливо, тому що $a\parallel b$ ). Зазначимо $C\in c$ так, щоб $BC\perp c$ , отже, $BC\perp b$ . Тоді $AC\perp c$ і $AC\perp a$ .
Справді, оскільки $AB\perp b, BC\perp b$ , то $b$ перпендикулярна площині (ABC\) . Оскільки $c\parallel a\parallel b$ , то прямі $a$ і $c$ теж перпендикулярні площині $ABC$ , а значить і будь-який прямий з цієї площини, зокрема, прямий \ (AC) .

Звідси слідує що $\angle BAC=\angle (\pi_1, \pi_2)$, $\angle ABC=\angle (\pi_2, \pi_3)=90^\circ$, $\angle BCA=\angle (\pi_3, \pi_1)$. Виходить, що $\triangle ABC$ прямокутний, отже \[\sin \angle BCA=\cos \angle BAC=0,2.\]

Відповідь: 0,2

Завдання 3 #2877

Рівень завдання: Складніше ЄДІ

Дано прямі $a, b, c$ , що перетинаються в одній точці, причому кут між будь-якими двома з них дорівнює $60^\circ$ . Знайдіть $\cos^(-1)\alpha$ , де $\alpha$ – кут між площиною, утвореною прямими $a$ і $c$ , і площиною, утвореною прямими $b$ ) і (c) . Відповідь дайте у градусах.

Нехай прямі перетинаються в точці (O). Так як кут між будь-якими двома з них дорівнює $60^\circ$, то всі три прямі не можуть лежати в одній площині. Зазначимо на прямій $a$ точку $A$ і проведемо $AB\perp b$ та $AC\perp c$ . Тоді $\triangle AOB=\triangle AOC$як прямокутні з гіпотенузи та гострого кута. Отже, $OB=OC$ і (AB=AC\) .
Проведемо $AH\perp (BOC)$. Тоді за теоремою про три перпендикуляри $HC\perp c$ , $HB\perp b$ . Оскільки $AB=AC$ , то $\triangle AHB=\triangle AHC$як прямокутні з гіпотенузи та катету. Отже, (HB = HC). Значить, $OH$ - бісектриса кута $BOC$ (оскільки точка $H$ рівновіддалена від сторін кута).

Зауважимо, що таким чином ми до того ж побудували лінійний кут двогранного кута, утвореного площиною, утвореною прямими (a) і (c), і площиною, утвореною прямими (b) і (c). Це кут (ACH).

Знайдемо цей кут. Оскільки точку (A) ми вибирали довільно, то нехай ми вибрали її так, що (OA = 2). Тоді в прямокутному $\triangle AOC$: \[\sin 60^\circ=\dfrac(AC)(OA) \quad\Rightarrow\quad AC=\sqrt3 \quad\Rightarrow\quad OC=\sqrt(OA^2-AC^2)=1.\ ]Так як $OH$ - бісектриса, то $\angle HOC=30^\circ$ , Отже, в прямокутному $\triangle HOC$ : \[\mathrm(tg)\,30^\circ=\dfrac(HC)(OC)\quad\Rightarrow\quad HC=\dfrac1(\sqrt3).\]Тоді з прямокутного $\triangle ACH$ : \[\cos\angle \alpha=\cos\angle ACH=\dfrac(HC)(AC)=\dfrac13 \quad\Rightarrow\quad \cos^(-1)\alpha=3.\]

Відповідь: 3

Завдання 4 #2910

Рівень завдання: Складніше ЄДІ

Площини $\pi_1$ і $\pi_2$ перетинаються по прямій $l$ , де лежать точки $M$ і $N$ . Відрізки $MA$ і $MB$ перпендикулярні до прямої $l$ і лежать у площинах $\pi_1$ і $\pi_2$ відповідно, причому $MN = 15$ , $AN = 39 $, \ (BN = 17 \), \ (AB = 40 \). Знайдіть $3\cos\alpha$ , де $\alpha$ - кут між площинами $\pi_1$ і $\pi_2$.

Трикутник $AMN$ прямокутний, $AN^2 = AM^2 + MN^2$, звідки \ Трикутник $BMN$ прямокутний, $BN^2 = BM^2 + MN^2$ , звідки \ Запишемо для трикутника $AMB$ теорему косінусів: \ Тоді \ Так як кут $\alpha$ між площинами - це гострий кут, а $\angle AMB$ вийшов тупим, то $\cos\alpha=\dfrac5(12)$ . Тоді \

Відповідь: 1,25

Завдання 5 #2911

Рівень завдання: Складніше ЄДІ

$ABCDA_1B_1C_1D_1$ – паралелепіпед, $ABCD$ – квадрат зі стороною $a$ , точка $M$ – основа перпендикуляра, опущеного з точки $A_1$ на площину $(ABCD)$ , крім того (M) - точка перетину діагоналей квадрата (ABCD). Відомо що $A_1M = \dfrac(\sqrt(3))(2)a$. Знайдіть кут між площинами $(ABCD)$ і $(AA_1B_1B)$ . Відповідь дайте у градусах.

Побудуємо (MN) перпендикулярно (AB) як показано на малюнку.

Так як $ABCD$ - квадрат зі стороною $a$ і $MNperp AB$ і $BCperp AB$ , то $MNparallel BC$ . Так як $M$ - точка перетину діагоналей квадрата, то $M$ - середина $AC$, отже, $MN$ - середня лінія і $MN =\frac12BC= \frac(1)(2)a$.
$MN$ – проекція $A_1N$ на площину $(ABCD)$ , причому $MN$ перпендикулярний $AB$ , тоді за теоремою про три перпендикуляри $A_1N$ перпендикулярний $AB $ і кут між площинами $(ABCD)$ і $(AA_1B_1B)$ є $\angle A_1NM$ .
\[\mathrm(tg)\, \angle A_1NM = \dfrac(A_1M)(NM) = \dfrac(\frac(\sqrt(3))(2)a)(\frac(1)(2)a) = \sqrt(3)\qquad\Rightarrow\qquad\angle A_1NM = 60^(\circ)\]

Відповідь: 60

Завдання 6 #1854

Рівень завдання: Складніше ЄДІ

У квадраті $ABCD$: $O$ - точка перетину діагоналей; $S$ - не лежить у площині квадрата, $SO \perp ABC$ . Знайдіть кут між площинами $ASD$ і $ABC$ , якщо $SO = 5$ , а $AB = 10$ .

Прямокутні трикутники $\triangle SAO$ і $\triangle SDO$ рівні по обидва боки і кут між ними ($SO \perp ABC$ $\Rightarrow$ $\angle SOA = \angle SOD = 90^\circ$; \ (AO = DO \), т.к. $O$ - точка перетину діагоналей квадрата, $SO$ - загальна сторона) $\Rightarrow$ $AS = SD$ $\Rightarrow$ $\triangle ASD$ - рівнобедрений. Точка $K$ - середина $AD$ , тоді $SK$ - висота в трикутнику $\triangle ASD$ , а $OK$ - висота в трикутнику $AOD$ $\ Rightarrow$ площина $SOK$ перпендикулярна площинам $ASD$ і $ABC$ $\Rightarrow$ $\angle SKO$ - лінійний кут, що дорівнює шуканому двогранному куту.

У $\triangle SKO$ : $OK = \frac(1)(2)\cdot AB = \frac(1)(2)\cdot 10 = 5 = SO$$\Rightarrow$ $\triangle SOK$ - рівнобедрений прямокутний трикутник $\Rightarrow$ $\angle SKO = 45^\circ$ .

Відповідь: 45

Завдання 7 #1855

Рівень завдання: Складніше ЄДІ

У квадраті $ABCD$: $O$ - точка перетину діагоналей; $S$ - не лежить у площині квадрата, $SO \perp ABC$ . Знайдіть кут між площинами $ASD$ і $BSC$ якщо $SO = 5$ , а $AB = 10$ .

Прямокутні трикутники $\triangle SAO$ , $\triangle SDO$ , $\triangle SOB$ і $\triangle SOC$ рівні по двох сторонах і кут між ними ($SO \perp ABC$ $\Rightarrow$ $\angle SOA = \angle SOD = \angle SOB = \angle SOC = 90^\circ$; \ (AO = OD = OB = OC \), т.к. $O$ - точка перетину діагоналей квадрата, $SO$ - загальна сторона) $\Rightarrow$ $AS = DS = BS = CS$ $\Rightarrow$ $\triangle ASD$ та $\triangle BSC$ - рівнобедрені. Точка $K$ - середина $AD$ , тоді $SK$ - висота в трикутнику $\triangle ASD$ , а $OK$ - висота в трикутнику $AOD$ $\ Rightarrow$ площина $SOK$ перпендикулярна площині $ASD$ . Точка $L$ - середина $BC$ , тоді $SL$ - висота в трикутнику $\triangle BSC$ , а $OL$ - висота в трикутнику $BOC$ $\ Rightarrow$ площина $SOL$ (вона ж площина $SOK$) перпендикулярна площині $BSC$. Таким чином отримуємо, що (angle KSL) - лінійний кут, рівний шуканому двогранному куті.

$KL = KO + OL = 2 \ cdot OL = AB = 10 $$\Rightarrow$ $OL = 5$; $SK = SL$ – висоти в рівних рівнобедрених трикутниках, які можна знайти за теоремою Піфагора: $SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50$. Можна помітити, що $SK^2 + SL^2 = 50 + 50 = 100 = KL^2$$\Rightarrow$ для трикутника $\triangle KSL$ виконується зворотна теорема Піфагора $\Rightarrow$ $\triangle KSL$ - прямокутний трикутник $\Rightarrow$ \(\angle KSL = 90^\ circ) .

Відповідь: 90

Підготовка учнів до здачі ЄДІ з математики, як правило, починається з повторення основних формул, у тому числі й тих, що дозволяють визначити кут між площинами. Незважаючи на те, що цей розділ геометрії досить докладно висвітлюється в рамках шкільної програми, багато випускників потребують повторення базового матеріалу. Розуміючи, як знайти кут між площинами, старшокласники зможуть оперативно вирахувати правильну відповідь у ході вирішення завдання та розраховувати на отримання гідних балів за підсумками складання єдиного державного іспиту.

Основні нюанси

Щоб питання, як знайти двогранний кут, не викликало труднощів, рекомендуємо дотримуватися алгоритму рішення, який допоможе впоратися із завданнями ЄДІ.

Спочатку необхідно визначити пряму, якою перетинаються площини.

Потім на цій прямій потрібно вибрати точку і провести до неї два перпендикуляри.

Наступний крок – знаходження тригонометричної функції двогранного кута, який утворений перпендикулярами. Робити це найзручніше за допомогою трикутника, що вийшов, частиною якого є кут.

Відповіддю буде значення кута або його тригонометричної функції.

Підготовка до екзаменаційного випробування разом зі «Школковим» - запорука вашого успіху

У процесі занять напередодні здачі ЄДІ багато школярів стикаються з проблемою пошуку визначень і формул, які дозволяють обчислити кут між двома площинами. Шкільний підручник не завжди є під рукою саме тоді, коли це потрібно. А щоб знайти потрібні формули та приклади їх правильного застосування, у тому числі і для знаходження кута між площинами в Інтернеті в режимі онлайн, часом потрібно витратити чимало часу.

Математичний портал «Школкове» пропонує новий підхід до підготовки до державного іспиту. Заняття на нашому сайті допоможуть учням визначити найскладніші для себе розділи та заповнити прогалини у знаннях.

Ми підготували та зрозуміло виклали весь необхідний матеріал. Базові визначення та формули представлені у розділі «Теоретична довідка».

Для того, щоб краще засвоїти матеріал, пропонуємо також попрактикуватися у виконанні відповідних вправ. Велика добірка завдань різного ступеня складності, наприклад, на , представлена розділ «Каталог». Усі завдання містять докладний алгоритм знаходження правильної відповіді. Перелік вправ на сайті постійно доповнюється та оновлюється.

Практикуючись у вирішенні завдань, у яких потрібно знайти кут між двома площинами, учні мають можливість в онлайн-режимі зберегти будь-яке завдання у «Вибраному». Завдяки цьому вони зможуть повернутися до нього необхідну кількість разів та обговорити хід його рішення зі шкільним учителем чи репетитором.

Поняття двогранного кута

Для введення поняття двогранного кута, спочатку згадаємо одну з аксіом стереометрії.

Будь-яку площину можна розділити на дві напівплощини прямої $a$, що лежить у цій площині. При цьому точки, що лежать в одній напівплощині знаходяться з одного боку від прямої $a$, а точки, що лежать у різних напівплощинах - по різні боки від прямої $a$ (рис. 1).

Малюнок 1.

На цій аксіомі заснований принцип побудови двогранного кута.

Визначення 1

Фігура називається двогранним кутомякщо вона складається з прямої і двох напівплощин цієї прямої, що не належать одній площині.

При цьому напівплощини двогранного кута називаються гранями, а пряма, що розділяє напівплощини - ребром двогранного кута(Рис. 1).

Малюнок 2. Двогранний кут

Градусний захід двогранного кута

Визначення 2

Виберемо на ребрі довільну точку $A$. Кут між двома прямими, що лежать у різних напівплощинах, перпендикулярних ребру і що перетинаються в точці $A$ називається лінійним кутом двогранного кута(Рис. 3).

Малюнок 3.

Вочевидь, кожен двогранний кут має нескінченне число лінійних кутів.

Теорема 1

Усі лінійні кути одного двогранного кута дорівнюють між собою.

Доведення.

Розглянемо два лінійні кути $AOB$ і $A_1(OB)_1$ (рис. 4).

Малюнок 4.

Оскільки промені $OA$ і $(OA)_1$ лежать у одній напівплощині $\alpha $ і перпендикулярні однієї прямої, всі вони є сонаправленными. Оскільки промені $OB$ і $(OB)_1$ лежать у одній напівплощині $\beta $ і перпендикулярні однієї прямої, вони є сонаправленными. Отже

\[\angle AOB=\angle A_1(OB)_1\]

Через довільність виборів лінійних кутів. Усі лінійні кути одного двогранного кута рівні між собою.

Теорему доведено.

Визначення 3

Градусною мірою двогранного кута називається градусна міра лінійного кута двогранного кута.

Приклади завдань

Приклад 1

Нехай нам дано дві неперпендикулярні площини $\alpha$ і $\beta$, які перетинаються по прямій $m$. Крапка $A$ належить площині $\beta$. $AB$ -- перпендикуляр до прямої $m$. $AC$ перпендикуляр до площини $\alpha$ (точка $C$ належить $\alpha$). Довести, що кут $ ABC є лінійним кутом двогранного кута.

Доведення.

Зобразимо малюнок за умовою задачі (рис. 5).

Малюнок 5.

Для доказу пригадаємо таку теорему

Теорема 2:Пряма, що проходить через основу похилої, перпендикулярна до неї, перпендикулярна до її проекції.

Оскільки $AC$ - перпендикуляр до площині $\alpha$, точка $C$ - проекція точки $A$ на площину $\alpha$. Отже, $BC$ - проекція похилої $AB$. За теоремою 2, $BC$ перпендикулярна ребру двогранного кута.

Тоді, кут $ABC$ відповідає всім вимогам визначення лінійного кута двогранного кута.

Приклад 2

Двогранний кут дорівнює $30^\circ$. На одній із граней лежить точка $A$, яка віддалена від іншої межі на відстань $4$ див. Знайти відстань від точки $A$ до ребра двогранного кута.

Рішення.

Розглянемо малюнок 5.

За умовою маємо $AC=4\ см$.

За визначенням градусної міри двогранного кута, маємо, що кут $ABC$ дорівнює $30^\circ$.

Трикутник $ABC$ є прямокутним трикутником. За визначенням синуса гострого кута

\[\frac(AC)(AB)=sin(30)^0\] \[\frac(5)(AB)=\frac(1)(2)\] \

Цей урок призначається для самостійного вивчення теми «Двогранний кут». У ході цього заняття учні познайомляться з однією з найважливіших геометричних фігур - двогранним кутом. Також на уроці нам доведеться дізнатися про те, як визначити лінійний кут геометричної фігури, що розглядається, і який буває двогранний кут при підставі фігури.

Повторимо, що таке кут на поверхні і як він вимірюється.

Мал. 1. Площина

Розглянемо площину (рис. 1). З точки Провиходять два промені - ОВі ОА.

Визначення. Фігура, утворена двома променями, що виходять із однієї точки, називається кутом.

Кут вимірюється в градусах та у радіанах.

Згадаймо, що таке радіан.

Мал. 2. Радіан

Якщо ми маємо центральний кут, довжина дуги якого дорівнює радіусу, такий центральний кут називається кутом в 1 радіан. , ∠ АОВ= 1 радий (рис. 2).

Зв'язок радіанів та градусів.

радий.

Отримуємо, радий. (). Тоді,

Визначення. Двогранним кутомназивається фігура, утворена прямою аі двома напівплощинами із спільним кордоном а, що не належать до однієї площини.

Мал. 3. Напівплощини

Розглянемо дві напівплощини α та β (рис. 3). Їхній спільний кордон - а. Зазначена фігура називається двогранним кутом.

Термінологія

Напівплощини α та β - це грані двогранного кута.

Пряма а- Це ребро двогранного кута.

На загальному ребрі адвогранного кута виберемо довільну точку Про(Рис. 4). У напівплощині з точки Провідновимо перпендикуляр ОАдо прямої а. З тієї ж точки Проу другій напівплощині β відновимо перпендикуляр ОВдо ребра а. Отримали кут АОВ, Який називається лінійним кутом двогранного кута.

Мал. 4. Вимірювання двогранного кута

Доведемо рівність всіх лінійних кутів для цього двогранного кута.

Нехай маємо двогранний кут (рис. 5). Виберемо крапку Проі точку Про 1на прямий а. Побудуємо лінійний кут відповідний точці Про, тобто проведемо два перпендикуляри ОАі ОВу площинах α та β відповідно до ребра а. Отримуємо кут АОВ- Лінійний кут двогранного кута.

Мал. 5. Ілюстрація доказу

З точки Про 1проведемо два перпендикуляри ОА 1і ВВ 1до ребра ау площинах α та β відповідно і отримаємо другий лінійний кут А 1 Про 1 В 1.

Промені О 1 А 1і ОАсонаправленны, тому що вони лежать в одній напівплощині і паралельні між собою як два перпендикуляри до однієї і тієї ж прямої а.

Аналогічно, промені О 1 В 1і ОВсонаправлены, отже, ∠ АОВ =∠ А 1 Про 1 В 1як кути із співспрямованими сторонами, що й потрібно було довести.

Площина лінійного кута перпендикулярна до ребра двогранного кута.

Довести: а ⊥ АОВ.

Мал. 6. Ілюстрація доказу

Доведення:

ОА ⊥ аз побудови, ОВ ⊥ аз побудови (рис. 6).

Отримуємо, що пряма аперпендикулярна двом прямим прямокутним прямим ОАі ОВз площини АОВотже, пряма аперпендикулярна площині ОАВ, що й потрібно було довести.

Двогранний кут вимірюється своїм лінійним кутом. Це означає, що скільки градусів радіан міститься в лінійному вугіллі, стільки ж градусів радіан міститься в його двогранному вугіллі. Відповідно до цього розрізняють такі види двогранних кутів.

Гострий (рис. 6)

Двогранний кут гострий, якщо лінійний кут гострий, тобто. .

Прямий (рис. 7)

Двогранний кут прямий, коли його лінійний кут дорівнює 90 ° - Тупий (рис. 8)

Двогранний кут тупий, що його лінійний кут тупий, тобто. .

Мал. 7. Прямий кут

Мал. 8. Тупий кут

Приклади побудови лінійних кутів у реальних фігурах

АВСD- Тетраедр.

1. Побудувати лінійний кут двогранного кута з ребром АВ.

Мал. 9. Ілюстрація до завдання

Побудова:

Йдеться про двогранний кут, який утворений рубом АВта гранями АВDі АВС(Рис. 9).

Проведемо пряму DНперпендикулярно до площини АВС, Н- основа перпендикуляра. Проведемо похилий DМперпендикулярно до прямої АВ,М- основа похилої. За теоремою про три перпендикуляри укладаємо, що проекція похилої НМтакож перпендикулярна до прямої АВ.

Тобто, з точки Мвідновлено два перпендикуляри до ребра АВу двох гранях АВDі АВС. Ми отримали лінійний кут DМН.

Зауважимо, що АВ, ребро двогранного кута, перпендикулярно площині лінійного кута, тобто площині DМН. Завдання вирішено.

Зауваження. Двогранний кут можна позначити так: DАВС, де

АВ- ребро, а крапки Dі Злежать у різних гранях кута.

2. Побудувати лінійний кут двогранного кута з ребром АС.

Проведемо перпендикуляр DНдо площини АВСі похилий DNперпендикулярно до прямої АС.За теоремою про три перпендикуляри отримуємо, що НN- проекція похилої DNна площину АВС,також перпендикулярна до прямої АС.DNН- Лінійний кут двогранного кута з ребром АС.

У тетраедрі DАВСусі ребра рівні. Крапка М- середина ребра АС. Доведіть, що кут DМВ- Лінійний кут двогранного кута ВАСD, Т. е. двогранного кута з ребром АС. Одна його грань АСD, друга - АСВ(Рис. 10).

Мал. 10. Ілюстрація до завдання

Рішення:

Трикутник ADC- рівносторонній, DM- Медіана, а значить і висота. Значить, DМ ⊥ АС.Аналогічно трикутник AУC- рівносторонній, УM- медіана, а отже, і висота. Значить, ВМ ⊥ АС.

Таким чином, з точки Мребра АСдвогранного кута відновлено два перпендикуляри DMі ВМдо цього ребра у гранях двогранного кута.

Значить, ∠ DMУ- Лінійний кут двогранного кута, що і потрібно довести.

Отже ми визначили двогранний кут, лінійний кут двогранного кута.

На наступному уроці ми розглянемо перпендикулярність прямих і площин, далі дізнаємося, що таке двогранний кут при підставі фігур.

Список літератури на тему "Двогранний кут", "Двогранний кут на основі геометричних фігур"

Геометрія. 10-11 клас: підручник для загальноосвітніх навчальних закладів / Шаригін І. Ф. – М.: Дрофа, 1999. – 208 с.: іл.
Геометрія. 10 клас: підручник для загальноосвітніх закладів з поглибленим та профільним вивченням математики /Є. В. Потоскуєв, Л. І. Звалич. – 6-те видання, стереотип. – М.: Дрофа, 2008. – 233 с.: іл.

Yaklass.ru ().
E-science.ru ().
Webmath.exponenta.ru().
Tutoronline.ru ().

Домашнє завдання на тему "Двогранний кут", визначення двогранного кута при основі фігур

Геометрія. 10-11 клас: підручник для учнів загальноосвітніх установ (базовий та профільний рівні) / І. М. Смирнова, В. А. Смирнов. – 5-е видання, виправлене та доповнене – М.: Мнемозіна, 2008. – 288 с.: іл.

Завдання 2, 3 стор. 67.

Що таке лінійний кут двогранного кута? Як його збудувати?

АВСD- Тетраедр. Побудувати лінійний кут двогранного кута з ребром:

а) УDб) DЗ.

АВСDA 1 B 1 C 1 D 1 - куб. Побудуйте лінійний кут двогранного кута А 1 АВСз ребром АВ. Визначте його градусну міру.

Двогранний кут. Лінійний кут двогранного кута. Двогранним кутом називається фігура, утворена двома напівплощинами, що не належать одній площині, що мають загальний кордон – пряму а. Напівплощини, що утворюють двогранний кут, називаються його гранями, а загальна межа цих напівплощин – рубом двогранного кута. Лінійним кутом двогранного кута називається кут, сторонами якого є промені, якими грані двогранного кута, перетинаються площиною, перпендикулярною ребру двогранного кута. У кожного двогранного кута скільки завгодно лінійних кутів: через кожну точку ребра можна провести площину, перпендикулярну до цього ребра; промені, якими ця площина перетинає грані двогранного кута, і утворюють лінійні кути.

Усі лінійні кути двогранного кута рівні між собою. Доведемо, що якщо рівні двогранні кути, утворені площиною основи піраміди КАВС і площин її бічних граней, то основа перпендикуляра, проведеного з вершини К, є центром вписаної в трикутник АВС кола.

Доведення. Насамперед, побудуємо лінійні кути рівних двогранних кутів. За визначенням, площина лінійного кута має бути перпендикулярна ребру двогранного кута. Отже, ребро двогранного кута має бути перпендикулярне сторонам лінійного кута. Якщо КО перпендикуляр до площини основи, то можна провести ОР перпендикуляр АС, OR перпендикуляр СВ, OQ перпендикулярAB, а потім з'єднати точки P, Q, R З точкою К. Тим самим ми побудуємо проекцію похилих РК, QK, RK так, що ребра АС, СВ, АВ перпендикулярні до цих проекцій. Отже, ці ребра перпендикулярні і самим похилим. І тому площини трикутників РОК, QOK, ROK перпендикулярні відповідним ребрам двогранного кута і утворюють рівні лінійні кути, про які сказано в умові. Прямокутні трикутники РОК, QOK, ROK рівні (оскільки вони мають загальний катет ОК і рівні протилежні цьому катету кути). Отже, ОР = OR = OQ. Якщо провести коло з центром О і радіусом ОР, то сторони трикутника АВС перпендикулярні радіусам ОР, OR і OQ тому є дотичні до цього кола.

Перпендикулярність площин. Площина альфа і бета називаються перпендикулярними, якщо лінійний кут одного з двогранних кутів, що утворилися при їх перетині дорівнює 90". Ознаки перпендикулярності двох площин Якщо одна з двох площин проходить через пряму, перпендикулярну до іншої площини, то ці площини перпендикулярні.

На малюнку зображено прямокутний паралелепіпед. Його основами є прямокутники ABCD і A1B1C1D1. А бічні ребра АА1 ВВ1, СС1, DD1 перпендикулярні до основ. Звідси випливає, що АА1 перпендикуляр АВ, тобто бічна грань - прямокутник. Таким чином, можна обґрунтувати властивості прямокутного паралелепіпеда: У прямокутному паралелепіпеді всі шість граней – прямокутники. У прямокутному паралелепіпеді всі шість граней – прямокутники. Усі двогранні кути прямокутного паралелепіпеда – прямі. Усі двогранні кути прямокутного паралелепіпеда – прямі.

Теорема Квадрат діагоналі прямокутного паралелепіпеда дорівнює сумі квадратів трьох його вимірів. Звернемося знову до малюнка, І доведемо, що АС12 =АВ2+AD2+АА12 Так як ребро СС1 перпендикулярне до основи АВСD то кут АСС1 прямий. З прямокутного трикутника АСС1 за теоремою Піфагора одержуємо АС12=АС2+СС12. Але АС – діагональ прямокутника АВСD, тому АС2 = АВ2+АD2. Крім того, СС1 = АА1. Отже, АС12= АВ2+АD2+AA12 Теорема доведена.