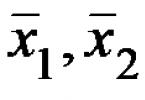Rice. 3.2Relative position of lines

Lines in space can occupy one of three positions relative to each other:

1) be parallel;

2) intersect;

3) interbreed.

Parallelare called straight lines that lie in the same plane and have no common points.

If the lines are parallel to each other, then on the CN their projections of the same name are also parallel (see section 1.2).

.

Intersectingare called straight lines that lie in the same plane and have one common point.

For intersecting lines on the CN, the projections of the same name intersect in the projections of the point A. Moreover, the frontal () and horizontal () projections of this point must be on the same communication line.

.

Crossbreedingare called lines that lie in parallel planes and have no common points.

If the lines are intersecting, then on the CN their projections of the same name can intersect, but the points of intersection of the projections of the same name will not lie on the same connection line.

In Fig. 3.4 point WITH belongs to the line b, and point D- straight A. These points are at the same distance from the frontal plane of projections. Similar to point E And F belong to different lines, but are at the same distance from the horizontal plane of projections. Therefore, on the CN their frontal projections coincide.

There are two possible cases of the location of a point relative to the plane: the point may belong to the plane or not belong to it (Fig. 3.5).

Sign of belonging of a point and a straight plane:

The point belongs to the plane, if it belongs to a line lying in this plane.

The straight line belongs to the plane, if it has two common points with it or has one common point with it and is parallel to another line lying in this plane.

In Fig. 3.5 shows a plane and points D And E. Dot D belongs to the plane because it belongs to the line l, which has two common points with this plane - 1 And A. Dot E does not belong to the plane, because it is impossible to draw a straight line through it lying in a given plane.

One of the problems for which level lines are used is the problem of constructing projections of a point belonging to a plane. Let there be a frontal projection D 2 of a point D belonging to the plane defined by the traces k X l (Fig. 111, a). You need to find the horizontal projection D 1 of point D.

A point belongs to a plane if it belongs to a line belonging to the plane. We solve the problem using the horizontal h of the k X l plane. Through point D 2 we draw a frontal projection h 2 of this horizontal line, which, as is known, should be parallel to the x 12 axis (Fig. 111 b). It will intersect the frontal projection k 2 of the frontal trace k to point N 2 ; Having drawn a vertical connection line, we find on the x 12 projection axis the horizontal projection of the frontal trace N of the horizontal (see Fig. 108).

TBegin-->TEnd-->

The horizontal projection h 1 of the horizontal must be parallel to l 1. We will find the horizontal projection D 1 of point D on the horizontal projection h 1 of the horizontal at the point of its intersection with the vertical connection line drawn through point D 2.

This problem could also be solved using the frontal. In this case, it would be necessary to draw a frontal projection f 2 ||k 2 through point D 2. We advise students to complete the construction themselves. The result should be the same as the first construction.

Let us slightly change the conditions of the problem. Let the horizontal projection E 1 of point E and the plane ABC, defined by the projections of the triangle (Fig. 112, a), be given. In this problem, you cannot use the horizontal of the plane, since there is no frontal projection of point E. We use the frontal f; through point E 1 we draw a horizontal projection (x frontal), find its frontal projection l2 and point E 1 on it.

A point in a plane can be constructed not only using the horizontal and frontal, but also using a straight line in general position. In some cases it is even more convenient.

TBegin-->
TEnd-->

The construction of a general line belonging to a general plane is not fundamentally different from the construction of horizontals and fronts belonging to the plane. The construction is based on a position known from geometry: a straight line belongs to a plane if it has two common points with this plane. Thus, if we intersect one of the projections of the plane with an arbitrary line and use two points of intersection of this line with lines belonging to the plane to construct a second projection of the line, then we can solve the problem. For example, let's solve the previous problem using a straight line in general position (Fig. 112, b). Through point E 1 we draw a straight line D 1 F 1 of any slope; we find the frontal projection D 2 F 2 of the DF line using the intersection points of D 1 and F 1. At the intersection of the frontal projection D 2 F 2 with the vertical communication line, we find the frontal projection E 1 of point E.

program schedule for today: Animal Planet, Bloomberg, Channel 3, CNN, Ajara TV, Classic Sport, Amazing Life, AB Moteurs Luxe HD, Jetix, Jetix Play, Mezzo, HD Cinema, Discovery Channel, MCM, MGM, HD Life, Discovery Science.

A point belongs to a line if its projections lie on the projections of the same name on this line (Fig. 21a).

A point belongs to a plane if it lies on a line lying in this plane (Fig. 21b).

A straight line belongs to a plane if it passes through two points lying in this plane (Fig. 21c).

A line is parallel to a plane if it is parallel to any line lying in that plane. Figure 22 shows a straight line t parallel to a straight line b belonging to the plane Σ: t // b О Σ (aÇ b).

Figure 22

Through any point in space you can draw an infinite number of lines parallel to a given plane.

This is a task to determine the common point of a line and a plane. It is also called the meeting point. Let us consider the intersection of a line with a plane of particular position.

The plane Σ is defined by the triangle ABC and is a horizontally projecting plane. The meeting point of straight line k with plane Σ is determined by the horizontal projection. The frontal projection of point K is completed using a communication line. The symbolic notation will look like this: k Ç Σ (ABC) = K.

The visibility of the line relative to the plane is determined using frontally competing points 1 and 2.

Figure 23

The intersection of a line with a general plane is shown in Figure 24. In this case, it is necessary to enclose the line in the projecting plane.

tО Σ ^ П 2 - straight line t belongs to the plane Σ, which is perpendicular to the horizontal plane of projections. The line of intersection of this plane with this one is line (1, 2). Then the point of intersection of this line with the straight line is found t, which will be the meeting point of the straight line and the plane. The visibility of a line relative to a plane is determined using competing points. Let's take horizontally competing points 3 and 4. Since point 3, which belongs to the line, turned out to be lower than point 4, therefore, the line on the horizontal plane to the right of the intersection point is invisible. Then we take frontally competing points 1 and 5. Point 1, which belongs to the plane, lies closer, therefore, the straight line is behind the plane, and it is invisible on the frontal projection from point 1 to point K.

Figure 24

The special straight lines belonging to the plane include the horizontal, frontal and profile straight lines. The construction of these lines is used in solving many problems in descriptive geometry. Their image is given in Figure 25. Moreover, on the horizontal plane the horizontal has a natural size, on the frontal plane - the frontal and on the profile plane - the profile straight line.

Figure 25

1. Formulate the conditions for a point to belong to a plane and a straight line to a plane.

2. How to construct a straight line parallel to a given plane?

3. Remember the stages of solving the problem of determining the point of intersection of a line and a plane.

4. What points are called competing?

5. How to draw horizontal and frontal lines in a plane?

6. What other special straight planes do you know?

Definition. A line and a plane are called parallel if they do not have common points (a ||)

A sign of parallelism between a line and a plane.

Theorem. If a line that does not lie in a given plane is parallel to some line that lies in this plane, then it is parallel to the plane itself.

Conclusions.

Cases of relative position of a straight line and a plane:

A) the straight line lies in the plane;
b) a straight line and a plane have only one common point;
c) a straight line and a plane do not have a single common point.

Cases of mutual arrangement of planes:

Properties of parallel planes:

Problems and tests on the topic "Topic 3. "Parallelism of a line and a plane; parallelism of planes."

• Parallelism of planes

  Lessons: 1 Assignments: 8 Tests: 1

• Parallelism of straight lines, line and plane - Parallelism of lines and planes, grade 10
• Signs of parallelism of two lines. Axiom of parallel lines - Parallel lines grade 7

  Lessons: 2 Assignments: 11 Tests: 1

• The relative position of lines in space. Angle between straight lines - Parallelism of lines and planes, grade 10

  Lessons: 1 Assignments: 9 Tests: 1

• Perpendicularity of a line and a plane - Perpendicularity of lines and planes, grade 10

  Lessons: 1 Assignments: 10 Tests: 1

The topic “Axioms of Stereometry” plays an important role in the development of spatial concepts, so try to involve more models (cardboard and knitting needles) and drawings.

The topic “Parallelism in Space” provides knowledge about the parallelism of lines and planes in space. This material summarizes information known from planimetry about the parallelism of straight lines. Using the example of the theorem on the existence and uniqueness of a line parallel to a given one, you get an idea of ​​the need to re-prove the facts known from planimetry in cases where we are talking about points and lines in space, and not about a specific plane.

Proof problems are solved in many cases by analogy with proving theorems. To solve problems on calculating the lengths of segments, it is necessary to repeat the planimetry course: equality and similarity of triangles, definitions, properties and characteristics of a rectangle, parallelogram, rhombus, square, trapezoid.

The signs of belonging are well known from the planimetry course. Our task is to consider them in relation to projections of geometric objects.

A point belongs to a plane if it belongs to a line lying in this plane.

Belonging to a straight plane is determined by one of two criteria:

a) a straight line passes through two points lying in this plane;

b) a line passes through a point and is parallel to lines lying in this plane.

Using these properties, let's solve the problem as an example. Let the plane be defined by a triangle ABC. It is required to construct the missing projection D 1 points D belonging to this plane. The sequence of constructions is as follows (Fig. 2.5).

Rice. 2.5. To construct projections of a point belonging to a plane

Through the point D 2 we carry out a straight line projection d, lying in the plane  ABC, intersecting one of the sides of the triangle and the point A 2. Then point 1 2 belongs to the lines A 2 D 2 and C 2 IN 2. Therefore, we can obtain its horizontal projection 1 1 onto C 1 IN 1 via communication line. Connecting points 1 1 and A 1, we get a horizontal projection d 1 . It's clear that the point D 1 belongs to it and lies on the line of projection connection with the point D 2 .

Problems of determining whether a point or a straight plane belongs to are solved quite simply. In Fig. Figure 2.6 shows the progress of solving such problems. For clarity of presentation of the problem, we define the plane by a triangle.

Rice. 2.6. Problems to determine whether a point belongs to a straight plane.

In order to determine whether a point belongs E plane  ABC, draw a straight line through its frontal projection E 2 A 2. Assuming that straight line a belongs to the plane  ABC, let's construct its horizontal projection A 1 at the intersection points 1 and 2. As we see (Fig. 2.6, a), straight A 1 does not pass through the point E 1 . Therefore, the point E ABC.

In the problem of belonging to a line V triangle planes ABC(Fig. 2.6, b), it is enough to use one of the straight line projections V 2 build another V 1 * considering that V ABC. As we see, V 1* and V 1 do not match. Therefore, straight V   ABC.

2.4. Level lines in a plane

The definition of level lines was given earlier. Level lines belonging to a given plane are called main . These lines (straight lines) play a significant role in solving a number of problems of descriptive geometry.

Let's consider constructing level lines in the plane defined by the triangle (Fig. 2.7).

Rice. 2.7. Constructing the main lines of a plane defined by a triangle

Horizontal plane  ABC we start by drawing its frontal projection h 2, which is known to be parallel to the axis OH. Since this horizontal line belongs to this plane, it passes through two points of the plane  ABC, namely, points A and 1. Having their frontal projections A 2 and 1 2, through the communication line we obtain horizontal projections ( A 1 already exists) 1 1 . Connecting the dots A 1 and 1 1 , we have a horizontal projection h 1 horizontal plane  ABC. Profile projection h 3 horizontal planes  ABC will be parallel to the axis OH a-priory.

Front plane  ABC is constructed in a similar way (Fig. 2.7) with the only difference that its drawing begins with a horizontal projection f 1, since it is known that it is parallel to the OX axis. Profile projection f 3 fronts must be parallel to the OZ axis and pass through the projections WITH 3, 2 3 of the same points WITH and 2.

Profile line of the plane  ABC has a horizontal R 1 and front R 2 projections parallel to the axes OY And OZ, and the profile projection R 3 can be obtained from the front using intersection points IN and 3 s  ABC.

When constructing the main lines of a plane, you need to remember only one rule: to solve the problem you always need to get two points of intersection with a given plane. The construction of main lines lying in a plane defined in a different way is no more complicated than that discussed above. In Fig. Figure 2.8 shows the construction of the horizontal and frontal planes defined by two intersecting straight lines A And V.

Rice. 2.8. Construction of the main lines of a plane defined by intersecting straight lines.